七年数学7.3 多边形及其内角和&7.4课题学习 镶嵌
文档属性
| 名称 | 七年数学7.3 多边形及其内角和&7.4课题学习 镶嵌 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-12 00:00:00 | ||
图片预览

文档简介
(共47张PPT)
7.3 多边形及其内角和
7.4 课题学习 镶嵌
情境引入
图中有你认识的多边形吗?
情境引入
图中有你认识的多边形吗?
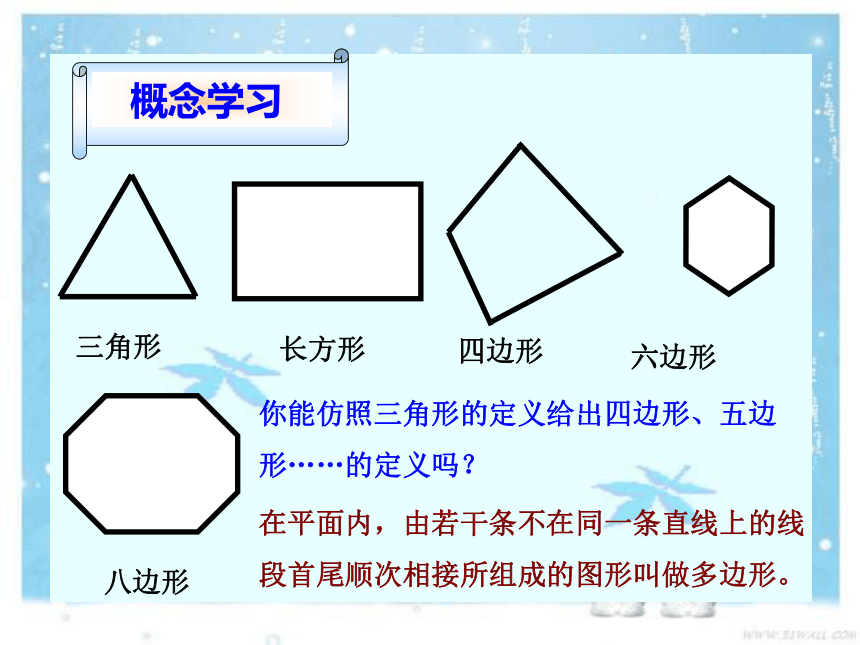
概念学习
三角形
长方形
六边形
四边形
八边形
在平面内,由若干条不在同一条直线上的线段首尾顺次相接所组成的图形叫做多边形。
你能仿照三角形的定义给出四边形、五边形……的定义吗?
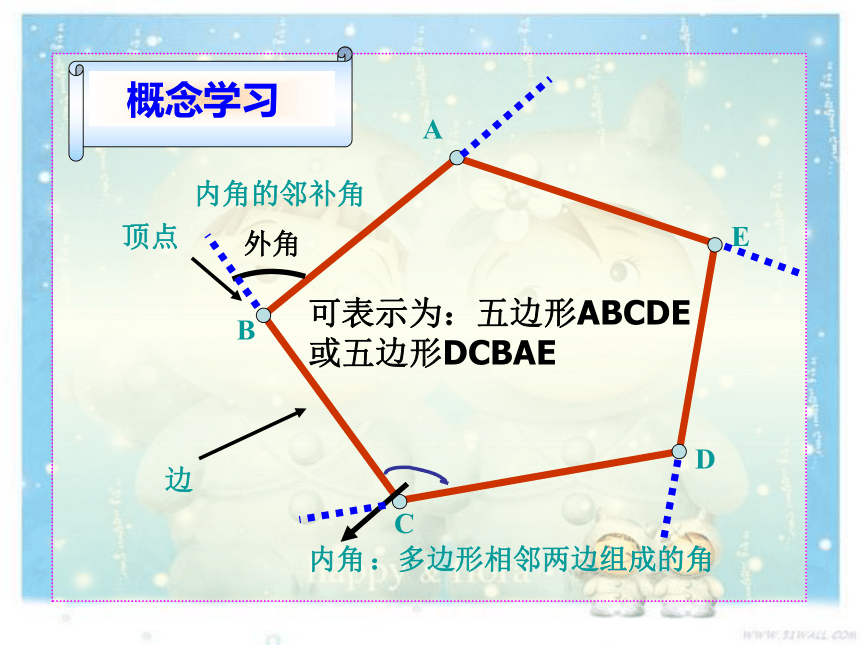
顶点
内角
边
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
概念学习
概念学习
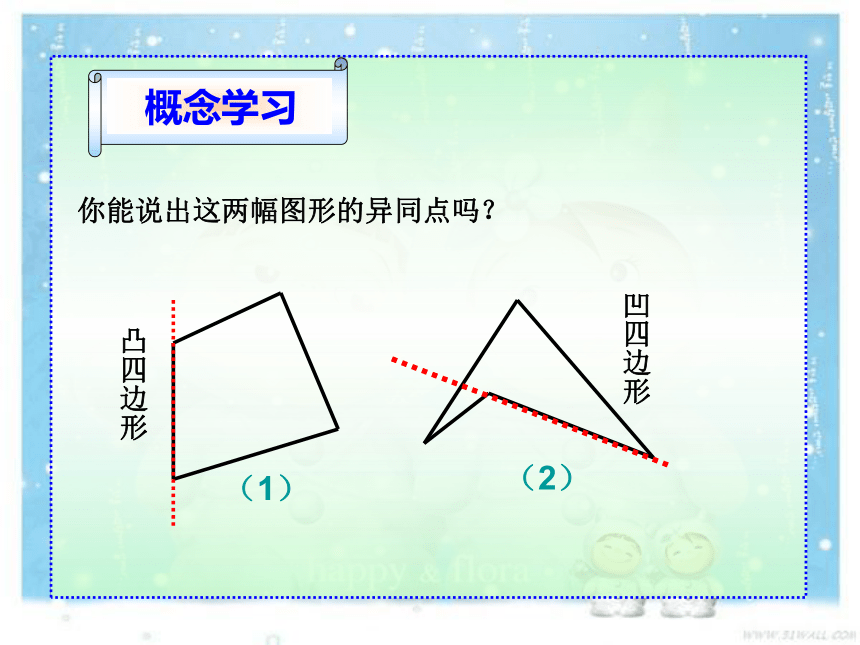
你能说出这两幅图形的异同点吗?
(1)
(2)
凸四边形
凹四边形
概念学习
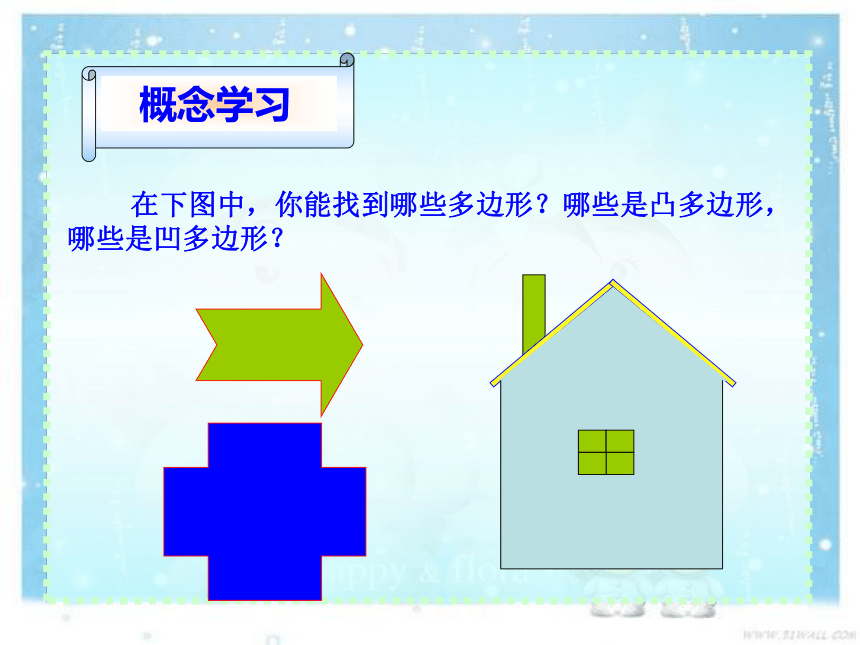
在下图中,你能找到哪些多边形?哪些是凸多边形,哪些是凹多边形?
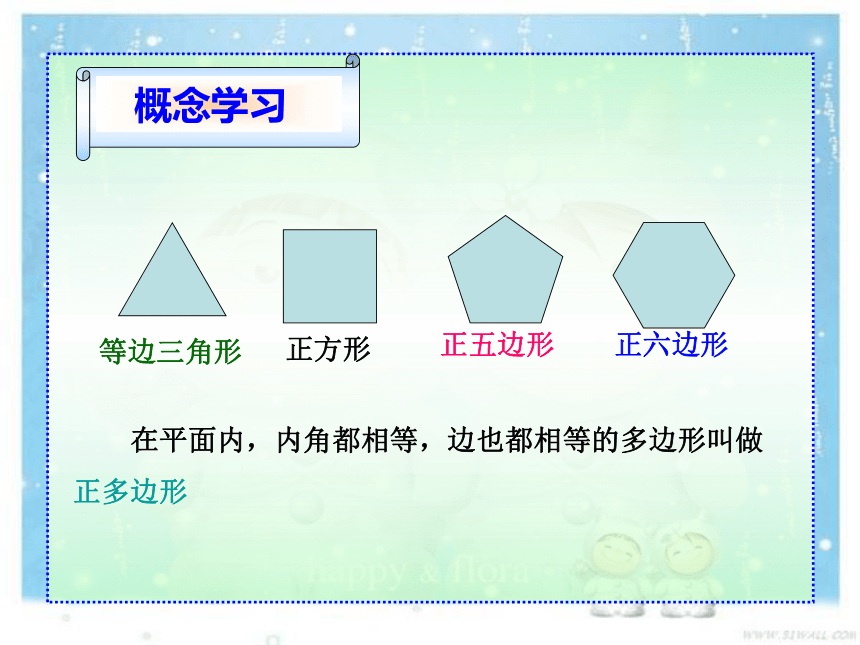
概念学面内,内角都相等,边也都相等的多边形叫做正多边形
等边三角形
正方形
正五边形
正六边形
概念学习
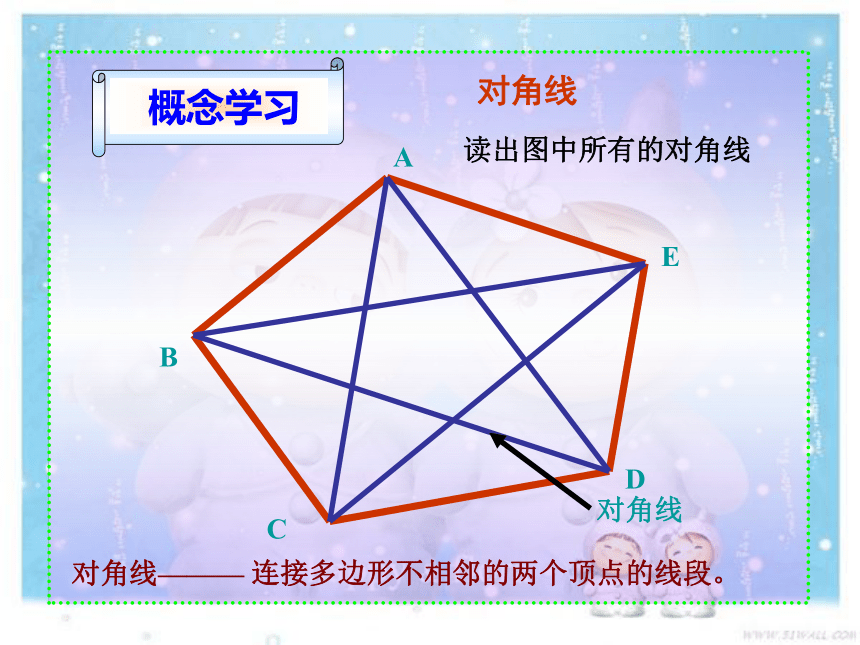
对角线
对角线
对角线——— 连接多边形不相邻的两个顶点的线段。
A
B
C
D
E
读出图中所有的对角线
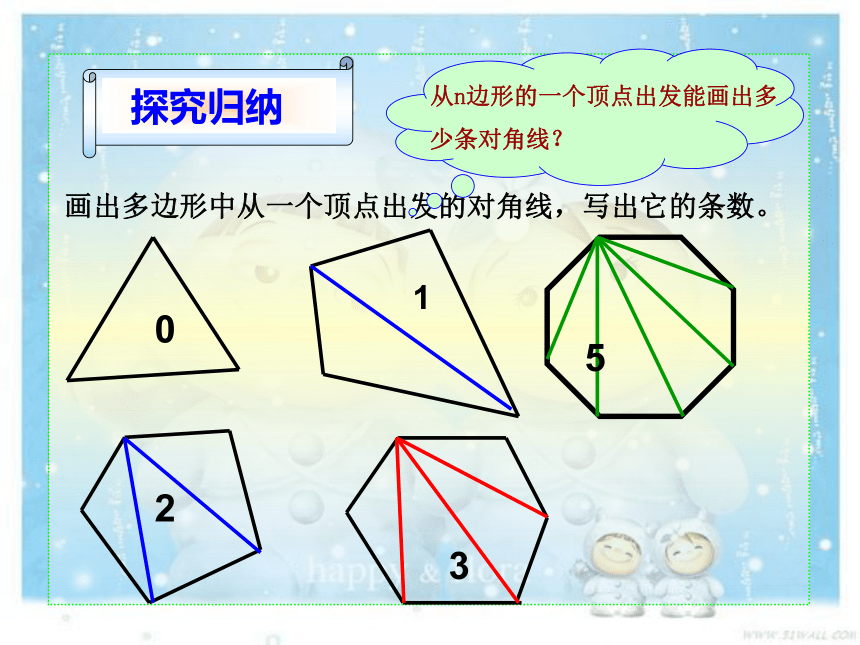
探究归纳
画出多边形中从一个顶点出发的对角线,写出它的条数。
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
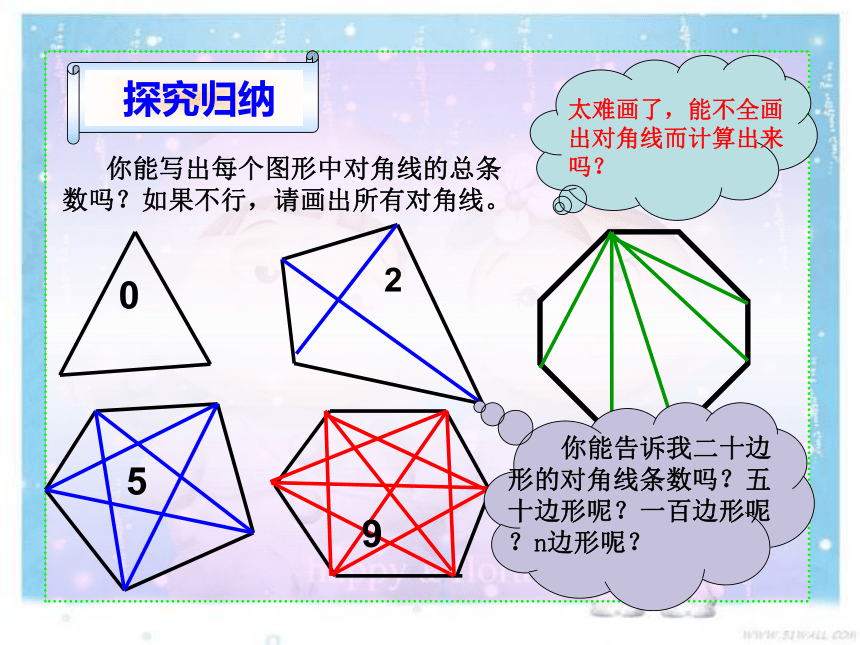
探究归纳
你能写出每个图形中对角线的总条数吗?如果不行,请画出所有对角线。
0
2
5
9
太难画了,能不全画出对角线而计算出来吗?
你能告诉我二十边形的对角线条数吗?五十边形呢?一百边形呢?n边形呢?
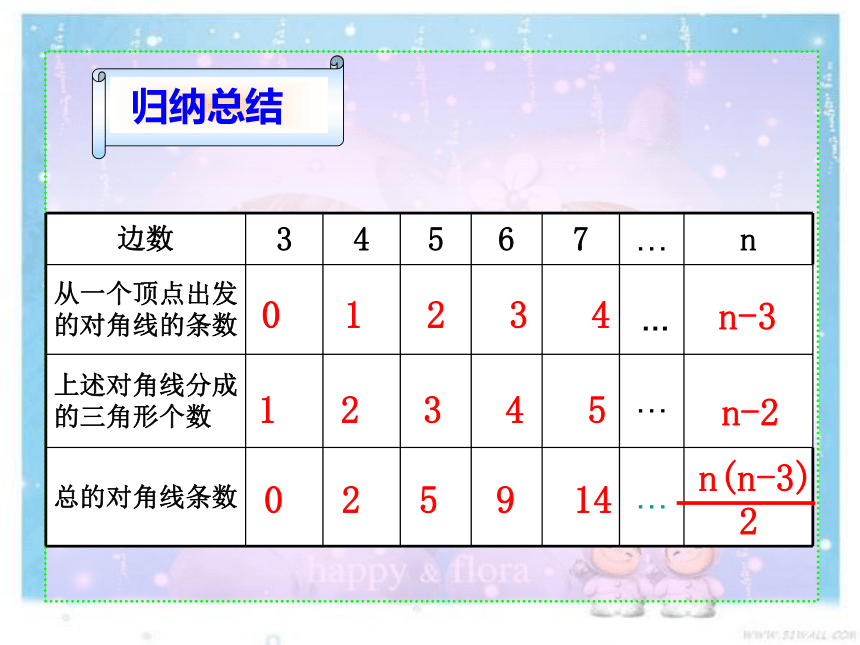
归纳总结
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
…
问题探究
多边形 边数 一个顶点出发的对角线条数 图形
分成三角形的个数 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
你能由下表归纳出多边形的内角和吗?
归纳总结
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°× 4 – 180° = 540°
问题探究
E
A
B
C
D
O
180°× 5 – 360°= 540°
问题探究
A
B
C
D
E
4 × 180°-180 °
O
=540°
问题探究
尝试应用
例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
解:四边形的内角和为:
(4-2) ×180 =360°
∴ ∠B+∠D= 360°- (∠ A+∠C)=180°
∠A+∠C=180°
尝试应用
十二边形的内角和是( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和是720°,则此多边形共有( )个内角。
如果一个多边形的内角和是1440度,那么这是( )边形。
1800°
180°
六
十
问题探究
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
6
E
B
C
D
1
2
3
4
5
A
五边形外角和
结论:五边形的外角和
等于360°
-(5-2) × 180°
=360°
=五个平角
-五边形内角和
=5×180°
探究交流
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
n边形的外角和等于360°
-(n-2)×180°
=360°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。
多边形的外角和
尝试应用
在行程中所转的各个角的和是多少?
尝试应用
正五边形的每一个外角等于____,每一个内角等于_____。
5x=360°
x=72°
72°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108°
108°
尝试应用
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360°,
∴ (n-2) 180°=2× 360°。
解得: n=6
∴这个多边形的边数为6。
拓展提高
(1)n边形的n个内角中锐角最多有______个
(2)把一个四边形削去一个角,剩下一个几边形?它的内角和是多少?
归纳整合
n边形内角和=(n-2)·180°
n边形的外角和等于360°
数学思想方法
转化思想—把多边形问题转化为三角形问题解决
归纳方法—由特殊到一般的进行归纳
情境引入
好平整的地板!这是怎么铺成的 怎么一点空隙也没有?
情境引入
好平整的地板!这是怎么铺成的 怎么一点空隙也没有?
我们经常能见到各种建筑物的地板,观察地板,就能发现地板常用各种多边形地砖铺砌成既没有缝隙又不重叠的美丽图案。
砖与砖严丝合缝,不留空隙、不重叠,并且把地面全部覆盖
概念学面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.
问题探究
仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
问题探究
正方形
正三角形
正六边形
问题探究
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
探究归纳
镶嵌满足的条件:
能铺满地面的多边形,围绕某一点的内角和为( )
360°
探究交流
思考:什么样的正多边形能够进行镶嵌
要用正多边形镶嵌成一个平面, 关键是:这种正多边形内角的度数能整除360°。
能单独镶嵌的正多边形有正三角形、正四边形、正六边形。
探究交流
用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
探究交流
60°×3+90°×2=360°
正三角形和正方形
探究交流
正三角形和正六边形
60°×4 +120°=360°
60°×2+120°×2=360°
探究交流
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
探究交流
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
探究交流
正方形和正六边形
探究交流
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
探究交流
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
1
3
2
探究交流
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
交流归纳
思考:只用形状、大小完全相同的任意五边形、六边形等能进行平面镶嵌吗 为什么
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
尝试应用
1.某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有( )种。
3
2.用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。 A.正方形 B.正六边形 C.正十二边形 D.正十八边形
D
归纳整合
(1)镶嵌的含义
(3)任意一种三角形,任意一种四边形都能镶嵌。
(2)镶嵌成平面图案的条件是:多边形围绕某一点的内角 和为360°
7.3 多边形及其内角和
7.4 课题学习 镶嵌
情境引入
图中有你认识的多边形吗?
情境引入
图中有你认识的多边形吗?
概念学习
三角形
长方形
六边形
四边形
八边形
在平面内,由若干条不在同一条直线上的线段首尾顺次相接所组成的图形叫做多边形。
你能仿照三角形的定义给出四边形、五边形……的定义吗?
顶点
内角
边
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
概念学习
概念学习
你能说出这两幅图形的异同点吗?
(1)
(2)
凸四边形
凹四边形
概念学习
在下图中,你能找到哪些多边形?哪些是凸多边形,哪些是凹多边形?
概念学面内,内角都相等,边也都相等的多边形叫做正多边形
等边三角形
正方形
正五边形
正六边形
概念学习
对角线
对角线
对角线——— 连接多边形不相邻的两个顶点的线段。
A
B
C
D
E
读出图中所有的对角线
探究归纳
画出多边形中从一个顶点出发的对角线,写出它的条数。
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
探究归纳
你能写出每个图形中对角线的总条数吗?如果不行,请画出所有对角线。
0
2
5
9
太难画了,能不全画出对角线而计算出来吗?
你能告诉我二十边形的对角线条数吗?五十边形呢?一百边形呢?n边形呢?
归纳总结
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数 …
总的对角线条数 …
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
…
问题探究
多边形 边数 一个顶点出发的对角线条数 图形
分成三角形的个数 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
你能由下表归纳出多边形的内角和吗?
归纳总结
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°× 4 – 180° = 540°
问题探究
E
A
B
C
D
O
180°× 5 – 360°= 540°
问题探究
A
B
C
D
E
4 × 180°-180 °
O
=540°
问题探究
尝试应用
例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
解:四边形的内角和为:
(4-2) ×180 =360°
∴ ∠B+∠D= 360°- (∠ A+∠C)=180°
∠A+∠C=180°
尝试应用
十二边形的内角和是( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和是720°,则此多边形共有( )个内角。
如果一个多边形的内角和是1440度,那么这是( )边形。
1800°
180°
六
十
问题探究
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
6
E
B
C
D
1
2
3
4
5
A
五边形外角和
结论:五边形的外角和
等于360°
-(5-2) × 180°
=360°
=五个平角
-五边形内角和
=5×180°
探究交流
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
n边形的外角和等于360°
-(n-2)×180°
=360°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。
多边形的外角和
尝试应用
在行程中所转的各个角的和是多少?
尝试应用
正五边形的每一个外角等于____,每一个内角等于_____。
5x=360°
x=72°
72°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108°
108°
尝试应用
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360°,
∴ (n-2) 180°=2× 360°。
解得: n=6
∴这个多边形的边数为6。
拓展提高
(1)n边形的n个内角中锐角最多有______个
(2)把一个四边形削去一个角,剩下一个几边形?它的内角和是多少?
归纳整合
n边形内角和=(n-2)·180°
n边形的外角和等于360°
数学思想方法
转化思想—把多边形问题转化为三角形问题解决
归纳方法—由特殊到一般的进行归纳
情境引入
好平整的地板!这是怎么铺成的 怎么一点空隙也没有?
情境引入
好平整的地板!这是怎么铺成的 怎么一点空隙也没有?
我们经常能见到各种建筑物的地板,观察地板,就能发现地板常用各种多边形地砖铺砌成既没有缝隙又不重叠的美丽图案。
砖与砖严丝合缝,不留空隙、不重叠,并且把地面全部覆盖
概念学面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做平面镶嵌.
问题探究
仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
问题探究
正方形
正三角形
正六边形
问题探究
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
探究归纳
镶嵌满足的条件:
能铺满地面的多边形,围绕某一点的内角和为( )
360°
探究交流
思考:什么样的正多边形能够进行镶嵌
要用正多边形镶嵌成一个平面, 关键是:这种正多边形内角的度数能整除360°。
能单独镶嵌的正多边形有正三角形、正四边形、正六边形。
探究交流
用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
探究交流
60°×3+90°×2=360°
正三角形和正方形
探究交流
正三角形和正六边形
60°×4 +120°=360°
60°×2+120°×2=360°
探究交流
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
探究交流
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
探究交流
正方形和正六边形
探究交流
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
探究交流
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
1
3
2
探究交流
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
交流归纳
思考:只用形状、大小完全相同的任意五边形、六边形等能进行平面镶嵌吗 为什么
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
尝试应用
1.某商店出售下列五种形状的地砖⑴正三角形、⑵正方形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有( )种。
3
2.用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )。 A.正方形 B.正六边形 C.正十二边形 D.正十八边形
D
归纳整合
(1)镶嵌的含义
(3)任意一种三角形,任意一种四边形都能镶嵌。
(2)镶嵌成平面图案的条件是:多边形围绕某一点的内角 和为360°
