2020-2021学年山东省潍坊市诸城市九年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省潍坊市诸城市九年级上学期期中数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 05:37:19 | ||
图片预览

文档简介
2020-2021学年山东省潍坊市诸城市九年级第一学期期中数学试卷
一、选择题(共12小题).
1.(3分)下列关于“圆”的说法不正确的是( )
A.圆是中心对称图形,圆心就是对称中心
B.垂直于弦的直径一定平分这条弦
C.相等的弧所对的弦一定相等,反过来,相等的弦所对的弧也一定相等
D.圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴
2.(3分)若锐角A满足cosA=,则∠A的度数是( )
A.30° B.45° C.60° D.75°
3.(3分)如图,已知△ABC的六个元素,其中a、b、c表示三角形三边的长,则下面甲、乙、丙、丁四个三角形中与△ABC不一定相似的图形是( )
A.甲 B.乙 C.丙 D.丁
4.(3分)在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化
5.(3分)如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是( )
A.2.5 B.3 C.3.5 D.4
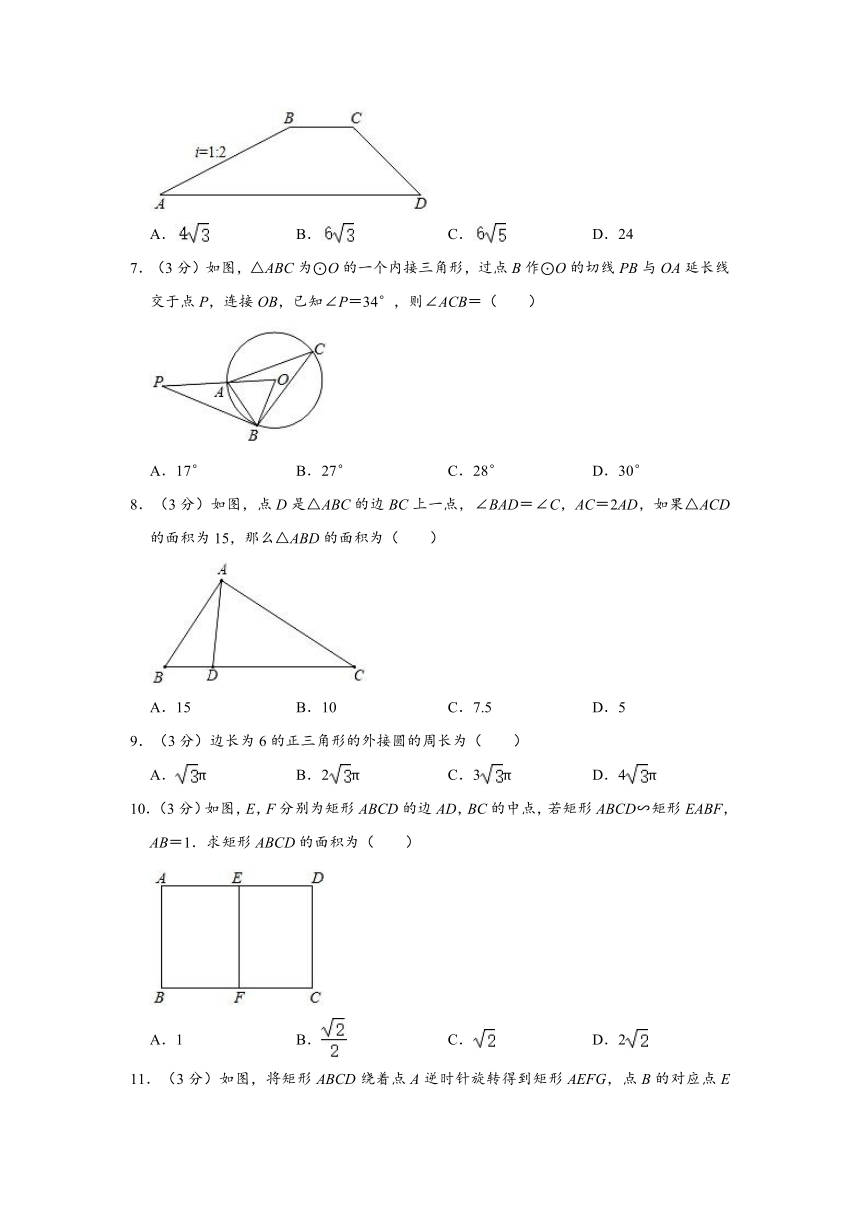
6.(3分)如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为( )
A. B. C. D.24
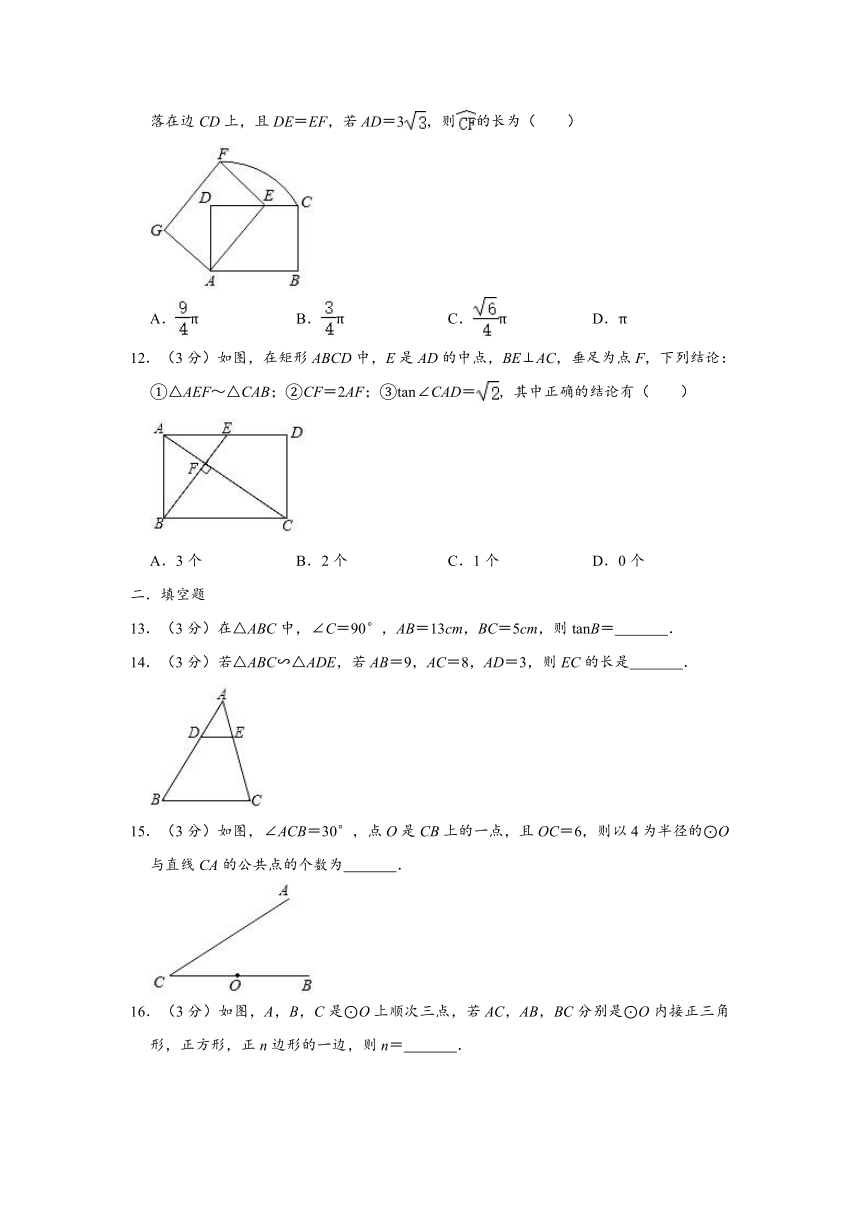
7.(3分)如图,△ABC为⊙O的一个内接三角形,过点B作⊙O的切线PB与OA延长线交于点P,连接OB,已知∠P=34°,则∠ACB=( )
A.17° B.27° C.28° D.30°
8.(3分)如图,点D是△ABC的边BC上一点,∠BAD=∠C,AC=2AD,如果△ACD的面积为15,那么△ABD的面积为( )
A.15 B.10 C.7.5 D.5
9.(3分)边长为6的正三角形的外接圆的周长为( )
A.π B.2π C.3π D.4π
10.(3分)如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积为( )
A.1 B. C. D.2
11.(3分)如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则的长为( )
A.π B.π C.π D.π
12.(3分)如图,在矩形ABCD中,E是AD的中点,BE⊥AC,垂足为点F,下列结论:①△AEF~△CAB;②CF=2AF;③tan∠CAD=,其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
二.填空题
13.(3分)在△ABC中,∠C=90°,AB=13cm,BC=5cm,则tanB= .
14.(3分)若△ABC∽△ADE,若AB=9,AC=8,AD=3,则EC的长是 .
15.(3分)如图,∠ACB=30°,点O是CB上的一点,且OC=6,则以4为半径的⊙O与直线CA的公共点的个数为 .
16.(3分)如图,A,B,C是⊙O上顺次三点,若AC,AB,BC分别是⊙O内接正三角形,正方形,正n边形的一边,则n= .
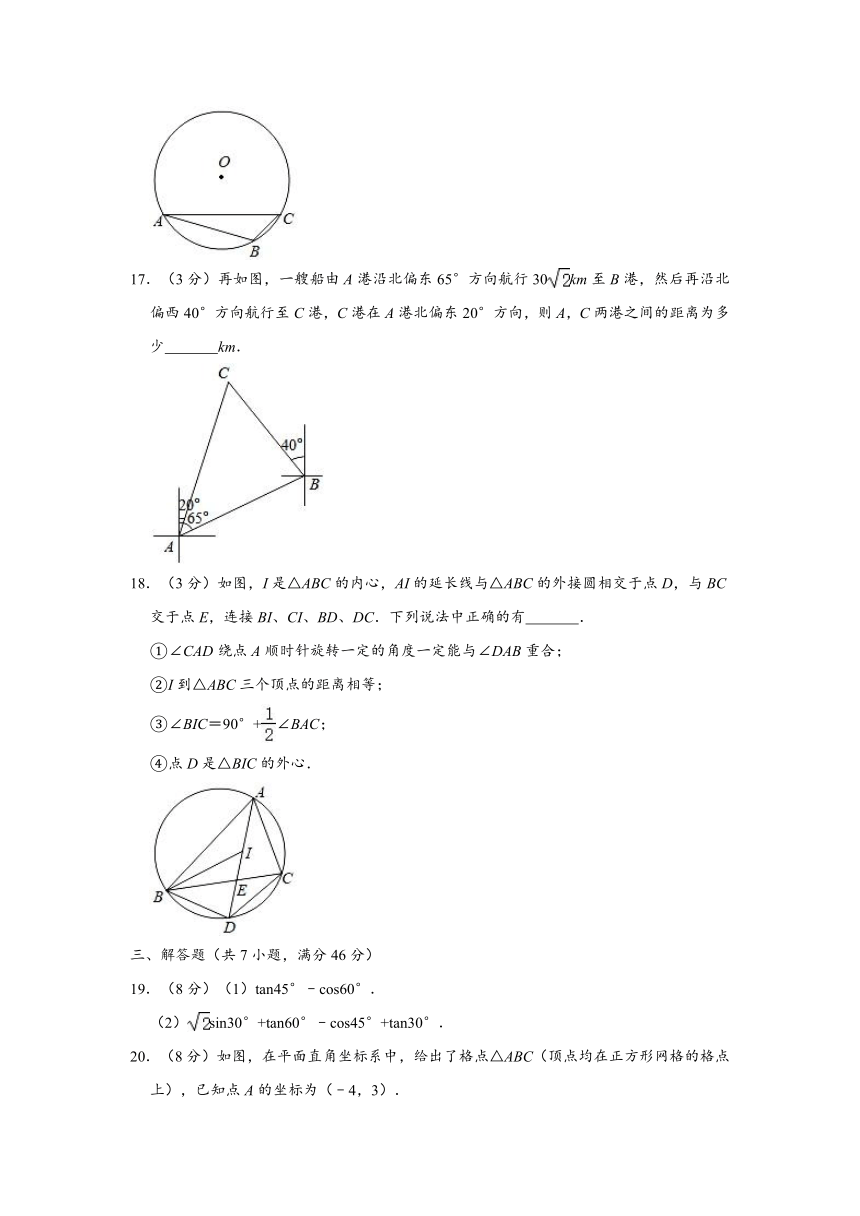
17.(3分)再如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为多少 km.
18.(3分)如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有 .
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;
③∠BIC=90°+∠BAC;
④点D是△BIC的外心.
三、解答题(共7小题,满分46分)
19.(8分)(1)tan45°﹣cos60°.
(2)sin30°+tan60°﹣cos45°+tan30°.
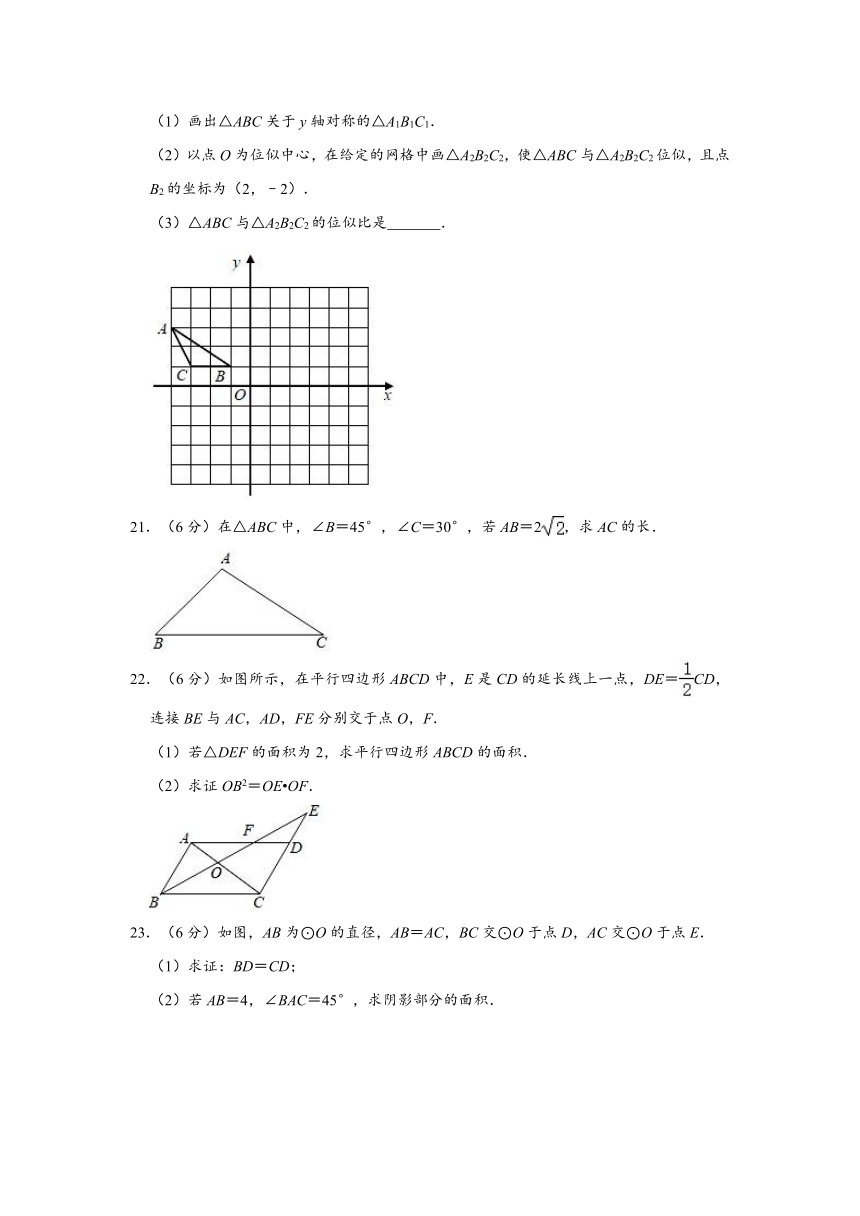
20.(8分)如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)以点O为位似中心,在给定的网格中画△A2B2C2,使△ABC与△A2B2C2位似,且点B2的坐标为(2,﹣2).
(3)△ABC与△A2B2C2的位似比是 .
21.(6分)在△ABC中,∠B=45°,∠C=30°,若AB=2,求AC的长.
22.(6分)如图所示,在平行四边形ABCD中,E是CD的延长线上一点,DE=CD,连接BE与AC,AD,FE分别交于点O,F.
(1)若△DEF的面积为2,求平行四边形ABCD的面积.
(2)求证OB2=OE?OF.
23.(6分)如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.
(1)求证:BD=CD;
(2)若AB=4,∠BAC=45°,求阴影部分的面积.
24.(6分)如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
25.(6分)如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
(1)证明:AC=AF;
(2)若AD=2,AF=,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
参考答案
一、选择题
1.(3分)下列关于“圆”的说法不正确的是( )
A.圆是中心对称图形,圆心就是对称中心
B.垂直于弦的直径一定平分这条弦
C.相等的弧所对的弦一定相等,反过来,相等的弦所对的弧也一定相等
D.圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴
解:A、圆是中心对称图形,圆心就是对称中心,故本选项正确;
B、垂直于弦的直径一定平分这条弦符合垂径定理,故本选项正确;
C、只有在同圆或等圆中,相等的弧所对的弦一定相等,反过来,相等的弦所对的弧也一定相等,故本小题错误;
D、圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴,故本选项正确.
故选:C.
2.(3分)若锐角A满足cosA=,则∠A的度数是( )
A.30° B.45° C.60° D.75°
解:∵cosA=,
∴∠A=30°.
故选:A.
3.(3分)如图,已知△ABC的六个元素,其中a、b、c表示三角形三边的长,则下面甲、乙、丙、丁四个三角形中与△ABC不一定相似的图形是( )
A.甲 B.乙 C.丙 D.丁
解:甲三角形的两边AC,BC的夹角不一定等于72度,故与△ABC不一定相似的图形,故选此选项正确;
乙可以利用两边对应成比例且夹角相等得出相似;
丙、丁可以利用两角对应相等得出相似;
故选:A.
4.(3分)在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化
解:根据锐角三角函数的概念,知
若各边长都扩大2倍,则sinA的值不变.
故选:D.
5.(3分)如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是( )
A.2.5 B.3 C.3.5 D.4
解:作OC⊥AB于点C,连接OA,如图所示:
则AC=AB=4,
∵OA=5,
∴OC===3,
则OP的最小值是3;
故选:B.
6.(3分)如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为( )
A. B. C. D.24
解:过B作BE⊥AD于E,过C作CF⊥AD于F,如图所示:
则四边形BEFC是矩形,
∴BE=CF,
∵背水坡CD的坡比i=1:1,CD=米,
∴CF=DF=CD=6(米),
∴BE=CF=6米,
又∵斜坡AB的坡比i=1:2=,
∴AE=2BE=12(米),
∴AB===6(米),
故选:C.
7.(3分)如图,△ABC为⊙O的一个内接三角形,过点B作⊙O的切线PB与OA延长线交于点P,连接OB,已知∠P=34°,则∠ACB=( )
A.17° B.27° C.28° D.30°
解:∵PB切⊙O于B,
∴OB⊥PB,
∴∠OBP=90°,
∵∠P=34°,
∴∠POB=180°﹣90°﹣34°=56°,
∴∠ACB=∠AOB=28°,
故选:C.
8.(3分)如图,点D是△ABC的边BC上一点,∠BAD=∠C,AC=2AD,如果△ACD的面积为15,那么△ABD的面积为( )
A.15 B.10 C.7.5 D.5
解:∵∠BAD=∠C,∠B=∠B,
∴△BAD∽△BCA,
∵AC=2AD,
∴=()2=,
∴=,
∵△ACD的面积为15,
∴△ABD的面积=×15=5,
故选:D.
9.(3分)边长为6的正三角形的外接圆的周长为( )
A.π B.2π C.3π D.4π
解:如图,⊙O为等边△ABC的外接圆,
作OD⊥BC于D,连接OB、OC,
∵△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=120°,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=CD=3,
在Rt△OBD中,OD=BD=,
∴OB=2OD=2,
∴⊙O的周长=2π×2=4π.
故选:D.
10.(3分)如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积为( )
A.1 B. C. D.2
解:由矩形ABCD∽矩形EABF可得,
设AE=x,则AD=BC=2x,又AB=1,
∴,
可得:,
∵矩形的长不能是负数,
解得:,
∴BC=2x=2×=,
∴S矩形ABCD=BC×AB=×1=.
故选:C.
11.(3分)如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则的长为( )
A.π B.π C.π D.π
解:连接AC、AF,
由旋转的性质可知,BC=EF,AB=AE,
∵DE=EF,
∴DE=BC=AD,
在Rt△ADE中,DE=AD,
∴∠DAE=45°,AE==3,
∴∠EAB=90°﹣45°=45°,即旋转角为45°,
∴∠FAC=45°,
在Rt△ABC中,AC===9,
∴的长==,
故选:A.
12.(3分)如图,在矩形ABCD中,E是AD的中点,BE⊥AC,垂足为点F,下列结论:①△AEF~△CAB;②CF=2AF;③tan∠CAD=,其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
解:如图,过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴=,
∵AE=AD=BC,
∴=,
∴CF=2AF,故②正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,
有=,即b=a,
∴tan∠CAD===,故③不正确;
正确的有①②,2个,
故选:B.
二.填空题
13.(3分)在△ABC中,∠C=90°,AB=13cm,BC=5cm,则tanB= .
解:由勾股定理得,AC===12,
∴tanB==,
故答案为:.
14.(3分)若△ABC∽△ADE,若AB=9,AC=8,AD=3,则EC的长是 .
解:设EC=x,
∵AC=8,
∴AE=8﹣x,
∵△ABC∽△ADE,
∴,
∴,
解得:x=,
故答案为:.
15.(3分)如图,∠ACB=30°,点O是CB上的一点,且OC=6,则以4为半径的⊙O与直线CA的公共点的个数为 2个 .
解:过O作OD⊥OA于D,
∵∠AOB=30°,OC=6,
∴OD=OC=3<4,
∴以4为半径的⊙O与直线CA的公共点的个数为2个,
故答案为:2个.
16.(3分)如图,A,B,C是⊙O上顺次三点,若AC,AB,BC分别是⊙O内接正三角形,正方形,正n边形的一边,则n= 12 .
解:如图,连接OA,OC,OB.
∵若AC、AB分别是⊙O内接正三角形、正方形的一边,
∴∠AOC=120°,∠AOB=90°,
∴∠BOC=∠AOC﹣∠AOB=30°,
由题意得30°=,
∴n=12,
故答案为:12.
17.(3分)再如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为多少 (30+10) km.
解:如图,过B作BE⊥AC于E,过C作CF∥AD,
则CF∥AD∥BG,∠AEB=∠CEB=90°,
∴∠ACF=∠CAD=20°,∠BCF=∠CBG=40°,
∴∠ACB=20°+40°=60°,
由题意得,∠CAB=65°﹣20°=45°,AB=30km,
在Rt△ABE中,∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∵AB=30km,
∴AE=BE=AB=30(km),
在Rt△CBE中,∵∠ACB=60°,tan∠ACB=,
∴CE===10(km),
∴AC=AE+CE=30+10(km),
∴A,C两港之间的距离为(30+10)km,
故答案为:(30+10).
18.(3分)如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有 ①③④ .
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;
③∠BIC=90°+∠BAC;
④点D是△BIC的外心.
解:∵I是△ABC的内心,
∴AD平分∠BAC,
即∠BAD=∠CAD,
∴∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合,所以①正确;
∵I是△ABC的内心,
∴点I到三角形三边的距离相等,所以②错误;
∵BI平分∠ABC,CI平分∠ACB,
∴∠1=∠ABC,∠ICB=∠ACB,
∵∠BIC=180°﹣∠1﹣∠ICB,
∴∠BIC=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,所以③正确;
∵∠1=∠2,∠3=∠CAD=∠4,
∴∠2+∠3=∠1+∠4,
而∠5=∠2+∠3,
∴∠5=∠1+∠4,即∠5=∠DBI,
∴DB=DI,
∵∠3=∠CAD,
∴=,
∴BD=CD,
∴DB=DI=DC,
∴点B、I、C在以点D为圆心,DB为半径的圆上,
即点D是△BIC的外心.所以④正确.
故答案为①③④.
三、解答题(共7小题,满分46分)
19.(8分)(1)tan45°﹣cos60°.
(2)sin30°+tan60°﹣cos45°+tan30°.
解:(1)原式=1﹣
=;
(2)原式=×+﹣+
=.
20.(8分)如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)以点O为位似中心,在给定的网格中画△A2B2C2,使△ABC与△A2B2C2位似,且点B2的坐标为(2,﹣2).
(3)△ABC与△A2B2C2的位似比是 1:2 .
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)△ABC与△A2B2C2的位似比是:1:2.
故答案为:1:2.
21.(6分)在△ABC中,∠B=45°,∠C=30°,若AB=2,求AC的长.
解:过A点作AD⊥BC于D点,
在直角三角形ABD中,∠B=45°,AB=2,
∴AD=AB?sinB=2,
在直角三角形ADC中,∠C=30°,
∴AC=2AD=4.
22.(6分)如图所示,在平行四边形ABCD中,E是CD的延长线上一点,DE=CD,连接BE与AC,AD,FE分别交于点O,F.
(1)若△DEF的面积为2,求平行四边形ABCD的面积.
(2)求证OB2=OE?OF.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,
∵DE=CD,
∴==,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴△DEF∽△ABF,
∴==,
又∵S△DEF=2,
∴S△ABF=8;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△DEF∽△CEB,
∴===,
∴S△CBE=9×2=18,
∴S四边形BCDF=S△CBE﹣S△DEF=18﹣2=16,
∴平行四边形ABCD的面积为:8+16=24.
(2)证明:∵AD∥BC,
∴△AOF∽△COB,
∴=,
∵AB∥DC,
∴△ABO∽△CEO,
∴=,
∴=,
∴OB2=OE?OF.
23.(6分)如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.
(1)求证:BD=CD;
(2)若AB=4,∠BAC=45°,求阴影部分的面积.
【解答】(1)证明:连结AD,
∵AB为⊙O直径,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD;
(2)解:连结OE,
∵AB=4,∠BAC=45°,
∴∠BOE=90°,BO=EO=2,∠AOE=90°,
∴S阴=S△BOE+S扇形OAE=×2×2+=π+2.
24.(6分)如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
解:由于BF=DB=2m,即∠D=45°,
∴DP=OP=灯高.
在△CEA与△COP中,
∵AE⊥CP,OP⊥CP,
∴AE∥OP.
∴△CEA∽△COP,
∴.
设AP=xm,OP=hm,则,①,
DP=OP=2+4+x=h,②
联立①②两式,
解得x=4,h=10.
∴路灯有10m高.
25.(6分)如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
(1)证明:AC=AF;
(2)若AD=2,AF=,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
【解答】(1)证明:∵四边形ABCD内接于⊙O,
∴∠ABC+∠ADC=180°.
∵∠ADF+∠ADC=180°,
∴∠ABC=∠ADF.
在△ABC与△ADF中,
,
∴△ABC≌△ADF(SAS).
∴AC=AF;
(2)解:由(1)得,AC=AF=.
∵AB=AD,
∴.
∴∠ADE=∠ACD.
∵∠DAE=∠CAD,
∴△ADE∽△ACD.
∴,
则AE===;
(3)证明:∵EG∥CF,
∴.
∴AG=AE.
由(2)得,
∴.
∵∠DAG=∠FAD,
∴△ADG∽△AFD.
∴∠ADG=∠F.
∵AC=AF,
∴∠ACD=∠F.
又∵∠ACD=∠ABD,
∴∠ADG=∠ABD.
∵BD为⊙O的直径,
∴∠BAD=90°.
∴∠ABD+∠BDA=90°.
∴∠ADG+∠BDA=90°.
∴GD⊥BD.
∴DG为⊙O的切线.
一、选择题(共12小题).
1.(3分)下列关于“圆”的说法不正确的是( )
A.圆是中心对称图形,圆心就是对称中心
B.垂直于弦的直径一定平分这条弦
C.相等的弧所对的弦一定相等,反过来,相等的弦所对的弧也一定相等
D.圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴
2.(3分)若锐角A满足cosA=,则∠A的度数是( )
A.30° B.45° C.60° D.75°
3.(3分)如图,已知△ABC的六个元素,其中a、b、c表示三角形三边的长,则下面甲、乙、丙、丁四个三角形中与△ABC不一定相似的图形是( )
A.甲 B.乙 C.丙 D.丁
4.(3分)在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化
5.(3分)如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是( )
A.2.5 B.3 C.3.5 D.4
6.(3分)如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为( )
A. B. C. D.24
7.(3分)如图,△ABC为⊙O的一个内接三角形,过点B作⊙O的切线PB与OA延长线交于点P,连接OB,已知∠P=34°,则∠ACB=( )
A.17° B.27° C.28° D.30°
8.(3分)如图,点D是△ABC的边BC上一点,∠BAD=∠C,AC=2AD,如果△ACD的面积为15,那么△ABD的面积为( )
A.15 B.10 C.7.5 D.5
9.(3分)边长为6的正三角形的外接圆的周长为( )
A.π B.2π C.3π D.4π
10.(3分)如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积为( )
A.1 B. C. D.2
11.(3分)如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则的长为( )
A.π B.π C.π D.π
12.(3分)如图,在矩形ABCD中,E是AD的中点,BE⊥AC,垂足为点F,下列结论:①△AEF~△CAB;②CF=2AF;③tan∠CAD=,其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
二.填空题
13.(3分)在△ABC中,∠C=90°,AB=13cm,BC=5cm,则tanB= .
14.(3分)若△ABC∽△ADE,若AB=9,AC=8,AD=3,则EC的长是 .
15.(3分)如图,∠ACB=30°,点O是CB上的一点,且OC=6,则以4为半径的⊙O与直线CA的公共点的个数为 .
16.(3分)如图,A,B,C是⊙O上顺次三点,若AC,AB,BC分别是⊙O内接正三角形,正方形,正n边形的一边,则n= .
17.(3分)再如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为多少 km.
18.(3分)如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有 .
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;
③∠BIC=90°+∠BAC;
④点D是△BIC的外心.
三、解答题(共7小题,满分46分)
19.(8分)(1)tan45°﹣cos60°.
(2)sin30°+tan60°﹣cos45°+tan30°.
20.(8分)如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)以点O为位似中心,在给定的网格中画△A2B2C2,使△ABC与△A2B2C2位似,且点B2的坐标为(2,﹣2).
(3)△ABC与△A2B2C2的位似比是 .
21.(6分)在△ABC中,∠B=45°,∠C=30°,若AB=2,求AC的长.
22.(6分)如图所示,在平行四边形ABCD中,E是CD的延长线上一点,DE=CD,连接BE与AC,AD,FE分别交于点O,F.
(1)若△DEF的面积为2,求平行四边形ABCD的面积.
(2)求证OB2=OE?OF.
23.(6分)如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.
(1)求证:BD=CD;
(2)若AB=4,∠BAC=45°,求阴影部分的面积.
24.(6分)如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
25.(6分)如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
(1)证明:AC=AF;
(2)若AD=2,AF=,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
参考答案
一、选择题
1.(3分)下列关于“圆”的说法不正确的是( )
A.圆是中心对称图形,圆心就是对称中心
B.垂直于弦的直径一定平分这条弦
C.相等的弧所对的弦一定相等,反过来,相等的弦所对的弧也一定相等
D.圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴
解:A、圆是中心对称图形,圆心就是对称中心,故本选项正确;
B、垂直于弦的直径一定平分这条弦符合垂径定理,故本选项正确;
C、只有在同圆或等圆中,相等的弧所对的弦一定相等,反过来,相等的弦所对的弧也一定相等,故本小题错误;
D、圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴,故本选项正确.
故选:C.
2.(3分)若锐角A满足cosA=,则∠A的度数是( )
A.30° B.45° C.60° D.75°
解:∵cosA=,
∴∠A=30°.
故选:A.
3.(3分)如图,已知△ABC的六个元素,其中a、b、c表示三角形三边的长,则下面甲、乙、丙、丁四个三角形中与△ABC不一定相似的图形是( )
A.甲 B.乙 C.丙 D.丁
解:甲三角形的两边AC,BC的夹角不一定等于72度,故与△ABC不一定相似的图形,故选此选项正确;
乙可以利用两边对应成比例且夹角相等得出相似;
丙、丁可以利用两角对应相等得出相似;
故选:A.
4.(3分)在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化
解:根据锐角三角函数的概念,知
若各边长都扩大2倍,则sinA的值不变.
故选:D.
5.(3分)如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是( )
A.2.5 B.3 C.3.5 D.4
解:作OC⊥AB于点C,连接OA,如图所示:
则AC=AB=4,
∵OA=5,
∴OC===3,
则OP的最小值是3;
故选:B.
6.(3分)如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为( )
A. B. C. D.24
解:过B作BE⊥AD于E,过C作CF⊥AD于F,如图所示:
则四边形BEFC是矩形,
∴BE=CF,
∵背水坡CD的坡比i=1:1,CD=米,
∴CF=DF=CD=6(米),
∴BE=CF=6米,
又∵斜坡AB的坡比i=1:2=,
∴AE=2BE=12(米),
∴AB===6(米),
故选:C.
7.(3分)如图,△ABC为⊙O的一个内接三角形,过点B作⊙O的切线PB与OA延长线交于点P,连接OB,已知∠P=34°,则∠ACB=( )
A.17° B.27° C.28° D.30°
解:∵PB切⊙O于B,
∴OB⊥PB,
∴∠OBP=90°,
∵∠P=34°,
∴∠POB=180°﹣90°﹣34°=56°,
∴∠ACB=∠AOB=28°,
故选:C.
8.(3分)如图,点D是△ABC的边BC上一点,∠BAD=∠C,AC=2AD,如果△ACD的面积为15,那么△ABD的面积为( )
A.15 B.10 C.7.5 D.5
解:∵∠BAD=∠C,∠B=∠B,
∴△BAD∽△BCA,
∵AC=2AD,
∴=()2=,
∴=,
∵△ACD的面积为15,
∴△ABD的面积=×15=5,
故选:D.
9.(3分)边长为6的正三角形的外接圆的周长为( )
A.π B.2π C.3π D.4π
解:如图,⊙O为等边△ABC的外接圆,
作OD⊥BC于D,连接OB、OC,
∵△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=120°,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=CD=3,
在Rt△OBD中,OD=BD=,
∴OB=2OD=2,
∴⊙O的周长=2π×2=4π.
故选:D.
10.(3分)如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积为( )
A.1 B. C. D.2
解:由矩形ABCD∽矩形EABF可得,
设AE=x,则AD=BC=2x,又AB=1,
∴,
可得:,
∵矩形的长不能是负数,
解得:,
∴BC=2x=2×=,
∴S矩形ABCD=BC×AB=×1=.
故选:C.
11.(3分)如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD=3,则的长为( )
A.π B.π C.π D.π
解:连接AC、AF,
由旋转的性质可知,BC=EF,AB=AE,
∵DE=EF,
∴DE=BC=AD,
在Rt△ADE中,DE=AD,
∴∠DAE=45°,AE==3,
∴∠EAB=90°﹣45°=45°,即旋转角为45°,
∴∠FAC=45°,
在Rt△ABC中,AC===9,
∴的长==,
故选:A.
12.(3分)如图,在矩形ABCD中,E是AD的中点,BE⊥AC,垂足为点F,下列结论:①△AEF~△CAB;②CF=2AF;③tan∠CAD=,其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
解:如图,过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴=,
∵AE=AD=BC,
∴=,
∴CF=2AF,故②正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,
有=,即b=a,
∴tan∠CAD===,故③不正确;
正确的有①②,2个,
故选:B.
二.填空题
13.(3分)在△ABC中,∠C=90°,AB=13cm,BC=5cm,则tanB= .
解:由勾股定理得,AC===12,
∴tanB==,
故答案为:.
14.(3分)若△ABC∽△ADE,若AB=9,AC=8,AD=3,则EC的长是 .
解:设EC=x,
∵AC=8,
∴AE=8﹣x,
∵△ABC∽△ADE,
∴,
∴,
解得:x=,
故答案为:.
15.(3分)如图,∠ACB=30°,点O是CB上的一点,且OC=6,则以4为半径的⊙O与直线CA的公共点的个数为 2个 .
解:过O作OD⊥OA于D,
∵∠AOB=30°,OC=6,
∴OD=OC=3<4,
∴以4为半径的⊙O与直线CA的公共点的个数为2个,
故答案为:2个.
16.(3分)如图,A,B,C是⊙O上顺次三点,若AC,AB,BC分别是⊙O内接正三角形,正方形,正n边形的一边,则n= 12 .
解:如图,连接OA,OC,OB.
∵若AC、AB分别是⊙O内接正三角形、正方形的一边,
∴∠AOC=120°,∠AOB=90°,
∴∠BOC=∠AOC﹣∠AOB=30°,
由题意得30°=,
∴n=12,
故答案为:12.
17.(3分)再如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为多少 (30+10) km.
解:如图,过B作BE⊥AC于E,过C作CF∥AD,
则CF∥AD∥BG,∠AEB=∠CEB=90°,
∴∠ACF=∠CAD=20°,∠BCF=∠CBG=40°,
∴∠ACB=20°+40°=60°,
由题意得,∠CAB=65°﹣20°=45°,AB=30km,
在Rt△ABE中,∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∵AB=30km,
∴AE=BE=AB=30(km),
在Rt△CBE中,∵∠ACB=60°,tan∠ACB=,
∴CE===10(km),
∴AC=AE+CE=30+10(km),
∴A,C两港之间的距离为(30+10)km,
故答案为:(30+10).
18.(3分)如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有 ①③④ .
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;
③∠BIC=90°+∠BAC;
④点D是△BIC的外心.
解:∵I是△ABC的内心,
∴AD平分∠BAC,
即∠BAD=∠CAD,
∴∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合,所以①正确;
∵I是△ABC的内心,
∴点I到三角形三边的距离相等,所以②错误;
∵BI平分∠ABC,CI平分∠ACB,
∴∠1=∠ABC,∠ICB=∠ACB,
∵∠BIC=180°﹣∠1﹣∠ICB,
∴∠BIC=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,所以③正确;
∵∠1=∠2,∠3=∠CAD=∠4,
∴∠2+∠3=∠1+∠4,
而∠5=∠2+∠3,
∴∠5=∠1+∠4,即∠5=∠DBI,
∴DB=DI,
∵∠3=∠CAD,
∴=,
∴BD=CD,
∴DB=DI=DC,
∴点B、I、C在以点D为圆心,DB为半径的圆上,
即点D是△BIC的外心.所以④正确.
故答案为①③④.
三、解答题(共7小题,满分46分)
19.(8分)(1)tan45°﹣cos60°.
(2)sin30°+tan60°﹣cos45°+tan30°.
解:(1)原式=1﹣
=;
(2)原式=×+﹣+
=.
20.(8分)如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(﹣4,3).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)以点O为位似中心,在给定的网格中画△A2B2C2,使△ABC与△A2B2C2位似,且点B2的坐标为(2,﹣2).
(3)△ABC与△A2B2C2的位似比是 1:2 .
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)△ABC与△A2B2C2的位似比是:1:2.
故答案为:1:2.
21.(6分)在△ABC中,∠B=45°,∠C=30°,若AB=2,求AC的长.
解:过A点作AD⊥BC于D点,
在直角三角形ABD中,∠B=45°,AB=2,
∴AD=AB?sinB=2,
在直角三角形ADC中,∠C=30°,
∴AC=2AD=4.
22.(6分)如图所示,在平行四边形ABCD中,E是CD的延长线上一点,DE=CD,连接BE与AC,AD,FE分别交于点O,F.
(1)若△DEF的面积为2,求平行四边形ABCD的面积.
(2)求证OB2=OE?OF.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,
∵DE=CD,
∴==,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴△DEF∽△ABF,
∴==,
又∵S△DEF=2,
∴S△ABF=8;
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△DEF∽△CEB,
∴===,
∴S△CBE=9×2=18,
∴S四边形BCDF=S△CBE﹣S△DEF=18﹣2=16,
∴平行四边形ABCD的面积为:8+16=24.
(2)证明:∵AD∥BC,
∴△AOF∽△COB,
∴=,
∵AB∥DC,
∴△ABO∽△CEO,
∴=,
∴=,
∴OB2=OE?OF.
23.(6分)如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.
(1)求证:BD=CD;
(2)若AB=4,∠BAC=45°,求阴影部分的面积.
【解答】(1)证明:连结AD,
∵AB为⊙O直径,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD;
(2)解:连结OE,
∵AB=4,∠BAC=45°,
∴∠BOE=90°,BO=EO=2,∠AOE=90°,
∴S阴=S△BOE+S扇形OAE=×2×2+=π+2.
24.(6分)如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
解:由于BF=DB=2m,即∠D=45°,
∴DP=OP=灯高.
在△CEA与△COP中,
∵AE⊥CP,OP⊥CP,
∴AE∥OP.
∴△CEA∽△COP,
∴.
设AP=xm,OP=hm,则,①,
DP=OP=2+4+x=h,②
联立①②两式,
解得x=4,h=10.
∴路灯有10m高.
25.(6分)如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
(1)证明:AC=AF;
(2)若AD=2,AF=,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
【解答】(1)证明:∵四边形ABCD内接于⊙O,
∴∠ABC+∠ADC=180°.
∵∠ADF+∠ADC=180°,
∴∠ABC=∠ADF.
在△ABC与△ADF中,
,
∴△ABC≌△ADF(SAS).
∴AC=AF;
(2)解:由(1)得,AC=AF=.
∵AB=AD,
∴.
∴∠ADE=∠ACD.
∵∠DAE=∠CAD,
∴△ADE∽△ACD.
∴,
则AE===;
(3)证明:∵EG∥CF,
∴.
∴AG=AE.
由(2)得,
∴.
∵∠DAG=∠FAD,
∴△ADG∽△AFD.
∴∠ADG=∠F.
∵AC=AF,
∴∠ACD=∠F.
又∵∠ACD=∠ABD,
∴∠ADG=∠ABD.
∵BD为⊙O的直径,
∴∠BAD=90°.
∴∠ABD+∠BDA=90°.
∴∠ADG+∠BDA=90°.
∴GD⊥BD.
∴DG为⊙O的切线.
同课章节目录
