2018-2019学年山东省泰安市东平县八年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2018-2019学年山东省泰安市东平县八年级上学期期中数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 05:34:51 | ||
图片预览



文档简介
2018-2019学年山东省泰安市东平县八年级第一学期期中数学试卷
一、选择题(共12小题).
1.(3分)已知a﹣b=1,则a2﹣b2﹣2b的值为( )
A.4 B.3 C.1 D.0
2.(3分)若的值为,则的值为( )
A. B. C. D..
3.(3分)已知x1,x2,…xn的平均数为5,方差为2,则3x1﹣2,3x2﹣2…3xn﹣2的平均数和方差分别是( )
A.13和18 B.13和4 C.5和18 D.5和4
4.(3分)如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
A.110° B.80° C.40° D.30°
5.(3分)如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a﹣b)等于( )
A.4 B.5 C.6 D.7
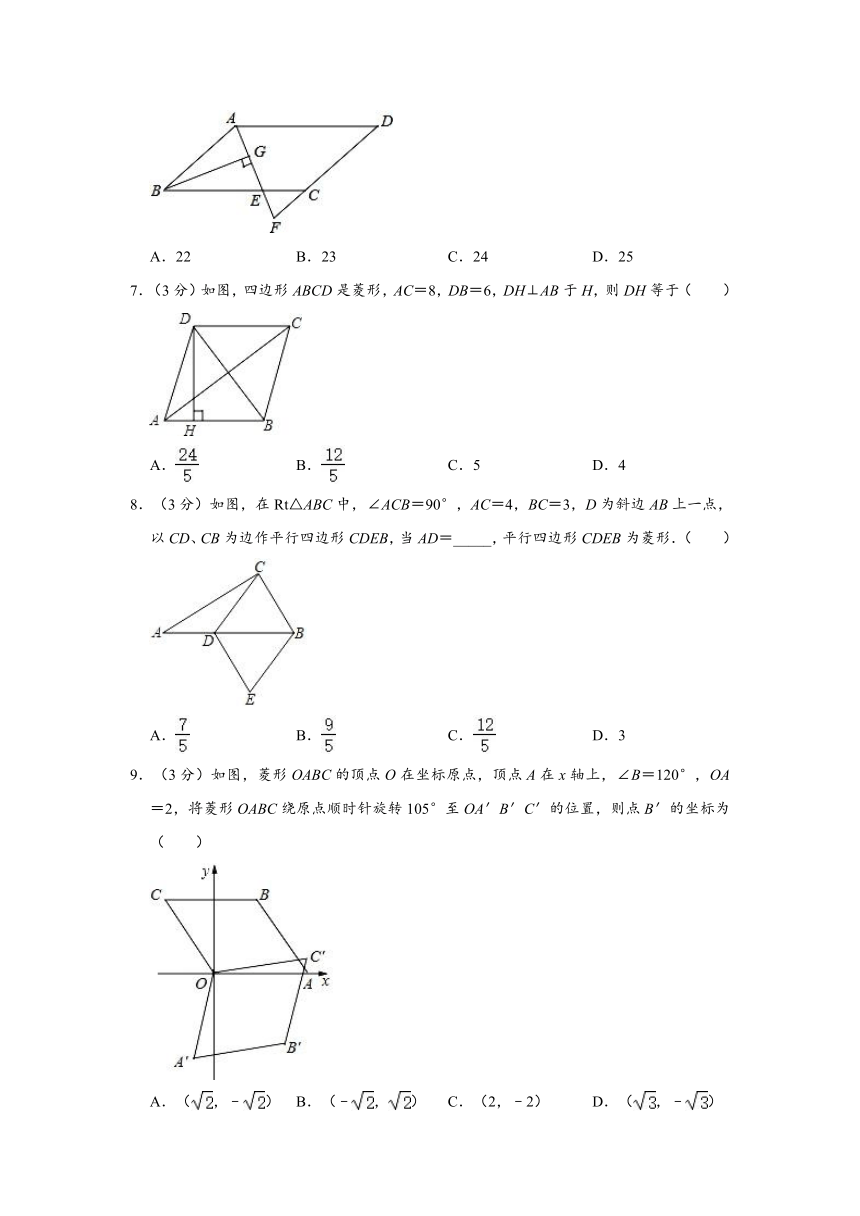
6.(3分)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
7.(3分)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
8.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=_____,平行四边形CDEB为菱形.( )
A. B. C. D.3
9.(3分)如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A.(,﹣) B.(﹣,) C.(2,﹣2) D.(,﹣)
10.(3分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A.3 B.4 C. D.
11.(3分)如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
12.(3分)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6个小题,每小题3分,共18分,把答案填在题中的横线上.)
13.(3分)已知m2+=51,则|m﹣|= .
14.(3分)若分式方程=5+有增根,则a的值为 .
15.(3分)如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为 .
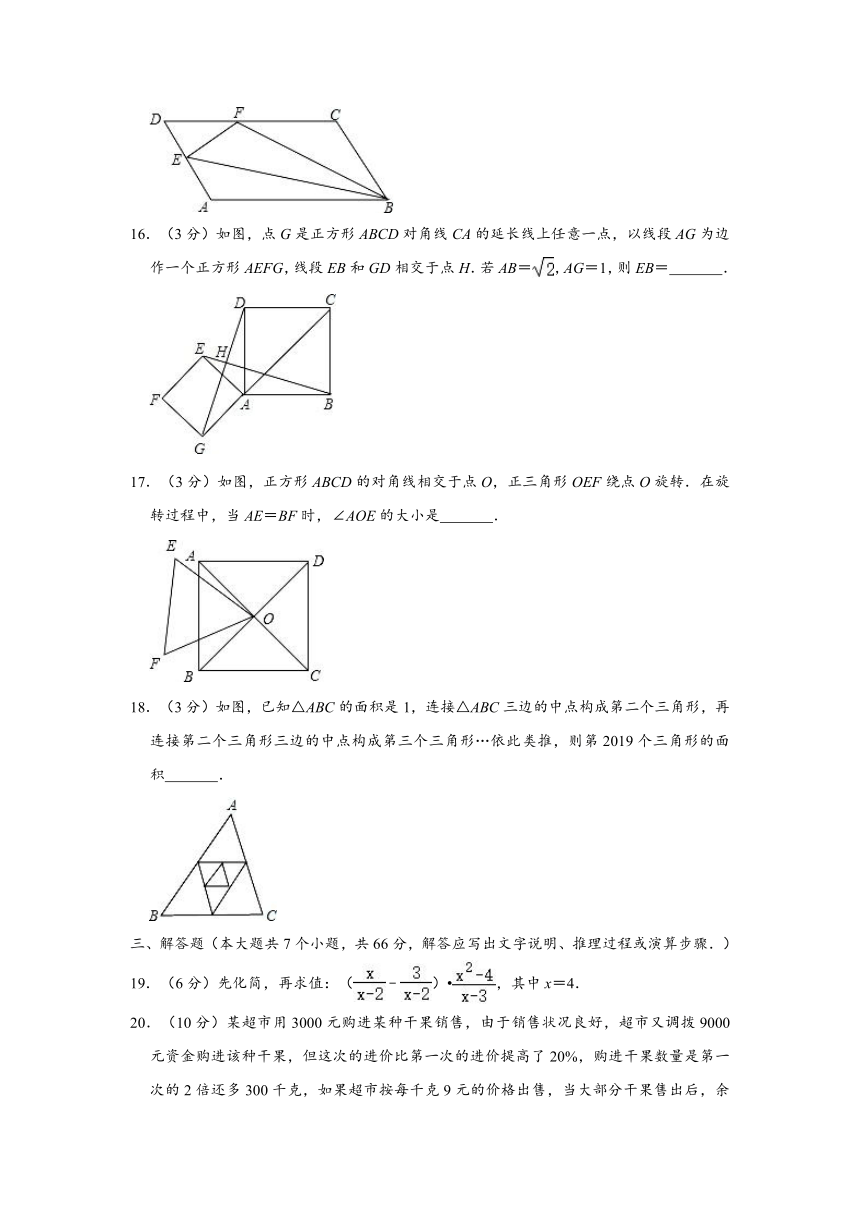
16.(3分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
17.(3分)如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转.在旋转过程中,当AE=BF时,∠AOE的大小是 .
18.(3分)如图,已知△ABC的面积是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2019个三角形的面积 .
三、解答题(本大题共7个小题,共66分,解答应写出文字说明、推理过程或演算步骤.)
19.(6分)先化简,再求值:(﹣)?,其中x=4.
20.(10分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
21.(8分)如图在△ABC中,以BC为边向三角形外做等边三角形△BCD,把△ABD绕D点按顺时针方向旋转60°后得到△ECD,且点A、C、E在同一条直线上,若AB=4,AC=2.
求:(1)∠ADE的度数;
(2)AD的长.
22.(8分)如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别交BC于点E,F,AE与DF相交于点G.
求证:(1)∠AGD=90°;
(2)BF=CE.
23.(10分)如图,在△ABC中,∠ABC=90°,BD为△ABC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG是菱形:
(2)若∠BAC=30°,BC=2,求四边形BDFG的面积.
24.(12分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)试探索OE与OF之间的数量关系.
(2)当点O运动到何处时,四边形AECF是矩形,并给出说理过程.
(3)在(2)的前提下,如果四边形AECF是正方形,那么△ABC将是什么三角形呢?请说明理由.
25.(12分)如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接DF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,求证:CE=PE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给予证明.
参考答案
一、选择题(本大题共12个小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求.)
1.(3分)已知a﹣b=1,则a2﹣b2﹣2b的值为( )
A.4 B.3 C.1 D.0
解:∵a﹣b=1,
∴a2﹣b2﹣2b=(a+b)(a﹣b)﹣2b
=a+b﹣2b
=a﹣b
=1.
故选:C.
2.(3分)若的值为,则的值为( )
A. B. C. D..
解:∵=,
∴2y2+3y=1,
∴原式===﹣.
故选:D.
3.(3分)已知x1,x2,…xn的平均数为5,方差为2,则3x1﹣2,3x2﹣2…3xn﹣2的平均数和方差分别是( )
A.13和18 B.13和4 C.5和18 D.5和4
解:∵x1,x2,…xn的平均数为5,
∴3x1﹣2,3x2﹣2…3xn﹣2的平均数是3×5﹣2=13,
∵x1,x2,…xn的方差为2,
∴3x1﹣2,3x2﹣2…3xn﹣2的方差是2×32=18.
故选:A.
4.(3分)如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
A.110° B.80° C.40° D.30°
解:根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,
∵∠A=40°,
∴∠A′=40°,
∵∠B′=110°,
∴∠A′CB′=180°﹣110°﹣40°=30°,
∴∠ACB=30°,
∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠ACA′=50°,
∴∠BCA′=30°+50°=80°,
故选:B.
5.(3分)如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a﹣b)等于( )
A.4 B.5 C.6 D.7
解:设重叠部分面积为c,
a﹣b=(a+c)﹣(b+c)=18﹣12=6,
故选:C.
6.(3分)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=9,CD=AB=6,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠AEB=∠BAE,
∴BE=AB=6,
∴CE=BC﹣BE=3,
∵BG⊥AE,
∴∠BGE=90°,AG=EG,
∴EG===2,
∴AE=2EG=4,
∴梯形AECD的周长=AE+CE+CD+AD=4+3+6+9=22,
故选:A.
7.(3分)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
解:∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB==5,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
8.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=_____,平行四边形CDEB为菱形.( )
A. B. C. D.3
解:如图,连接CE交AB于点O.
∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB===5.
若平行四边形CDEB为菱形时,CE⊥BD,且OD=OB,CD=CB.
∵S△ACB=AB?OC=AC?BC,
∴OC=.
∴在Rt△BOC中,根据勾股定理得,OB===,
∴AD=AB﹣2OB=.
故选:A.
9.(3分)如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A.(,﹣) B.(﹣,) C.(2,﹣2) D.(,﹣)
解:连接OB,OB′,过点B′作B′E⊥x轴于E,
根据题意得:∠BOB′=105°,
∵四边形OABC是菱形,
∴OA=AB,∠AOB=∠AOC=∠ABC=×120°=60°,
∴△OAB是等边三角形,
∴OB=OA=2,
∴∠AOB′=∠BOB′﹣∠AOB=105°﹣60°=45°,OB′=OB=2,
∴OE=B′E=OB′?sin45°=2×=,
∴点B′的坐标为:(,﹣).
故选:A.
10.(3分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A.3 B.4 C. D.
解:∵CE=5,△CEF的周长为18,
∴CF+EF=18﹣5=13.
∵F为DE的中点,
∴DF=EF.
∵∠BCD=90°,
∴CF=DE,
∴EF=CF=DE=6.5,
∴DE=2EF=13,
∴CD=.
∵四边形ABCD是正方形,
∴BC=CD=12,O为BD的中点,
∴OF是△BDE的中位线,
∴OF=(BC﹣CE)=(12﹣5)=.
故选:D.
11.(3分)如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB?BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=×5×PE+×5×PF=(PE+PF)=12,
解得:PE+PF=4.8.
故选:A.
12.(3分)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
解:作F点关于BD的对称点F′,连接EF′交BD于点P,则PF=PF′.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=DF′=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故选:C.
二、填空题(本大题共6个小题,每小题3分,共18分,把答案填在题中的横线上.)
13.(3分)已知m2+=51,则|m﹣|= 7 .
解:∵m2+=51,
∴m2+﹣2=51﹣2,即(m﹣)2=49,
则|m﹣|=7,
故答案为:7.
14.(3分)若分式方程=5+有增根,则a的值为 4 .
解:去分母得:x=5x﹣20+a,
由分式方程有增根,得到x﹣4=0,即x=4,
把x=4代入整式方程得:4=20﹣20+a,
解得:a=4,
故答案为:4.
15.(3分)如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为 7 .
解:由折叠的性质可得EF=AE、BF=AB,
∴?ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=8+22=30,
∵四边形ABCD为平行四边形,
∴AB+BC=15,
∵△FCB的周长=CF+BC+BF=CF+BC+AB=22,
即FC+15=22,
∴FC=7,
故答案为7.
16.(3分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
解:连接BD交AC于O,
∵四边形ABCD、AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG,
∴∠EAB=∠GAD,
在△AEB和△AGD中,
,
∴△EAB≌△GAD(SAS),
∴EB=GD,
∵四边形ABCD是正方形,AB=,
∴BD⊥AC,AC=BD=AB=2,
∴∠DOG=90°,OA=OD=BD=1,
∵AG=1,
∴OG=OA+AG=2,
∴GD==,
∴EB=.
故答案为:.
17.(3分)如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转.在旋转过程中,当AE=BF时,∠AOE的大小是 15°或165° .
解:连结AE、BF,
如图1,
∵四边形ABCD为正方形,
∴OA=OB,∠AOB=90°,
∵△OEF为等边三角形,
∴OE=OF,∠EOF=60°,
∵在△OAE和△OBF中
,
∴△OAE≌△OBF(SSS),
∴∠AOE=∠BOF=(90°﹣60°)=15°,
如图2,
∵在△AOE和△BOF中
,
∴△AOE≌△BOF(SSS),
∴∠AOE=∠BOF,
∴∠DOF=∠COE,
∴∠DOF=(90°﹣60°)=15°,
若F点在E点上方,则∠AOE=180°﹣15°=165°;
∴∠AOE大小为15°或165°.
故答案为15°或165°.
18.(3分)如图,已知△ABC的面积是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2019个三角形的面积 ()2018 .
解:∵D、E、F分别为AB、BC、AC的中点,
∴DE、EF、DF分别为△ABC的中位线,
∴DE=AC,DF=BC,EF=AB,
作AG⊥DE于G,交BC于H,则AG=GH,
∵△ABC的面积=BC×AH,△DEF的面积=DE×GH,
∴△DEF的面积=△ABC的面积=,
同理:第三个三角形的面积=△DEF的面积==()2,第四个三角形的面积=第三个三角形面积=()3,……,
∴第2019个三角形的面积为()2018,
故答案为:()2018.
三、解答题(本大题共7个小题,共66分,解答应写出文字说明、推理过程或演算步骤.)
19.(6分)先化简,再求值:(﹣)?,其中x=4.
解:原式=?
=x+2,
当x=4时,原式=6.
20.(10分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,
由题意,得=2×+300,
解得x=5,
经检验x=5是原方程的解.
答:该种干果的第一次进价是每千克5元;
(2)[+﹣600]×9+600×9×80%﹣(3000+9000)
=(600+1500﹣600)×9+4320﹣12000
=1500×9+4320﹣12000
=13500+4320﹣12000
=5820(元).
答:超市销售这种干果共盈利5820元.
21.(8分)如图在△ABC中,以BC为边向三角形外做等边三角形△BCD,把△ABD绕D点按顺时针方向旋转60°后得到△ECD,且点A、C、E在同一条直线上,若AB=4,AC=2.
求:(1)∠ADE的度数;
(2)AD的长.
解:(1)△ABD绕D点按顺时针方向旋转60°后得到△ECD,
∴∠ADE=60°.
(2)△ABD绕D点按顺时针方向旋转60°后得到△ECD,
∴∠ADE=60°,AD=DE,
∴△AED为等边三角形,
又∵CE=BA=4,AC=2,
∴AE=6,
∴AD=6.
22.(8分)如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别交BC于点E,F,AE与DF相交于点G.
求证:(1)∠AGD=90°;
(2)BF=CE.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴∠BAD+∠ADC=180°.
∵AE,DF分别平分∠BAD,∠ADC,
∴∠DAG=∠BAD,∠ADG=∠ADC.
∴∠DAG+∠ADG=×180°=90°.
∴∠AGD=180°﹣90°=90°.
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
同理DC=CF,
又∵AB=CD,
∴BE=CF,
∴BF=CE.
23.(10分)如图,在△ABC中,∠ABC=90°,BD为△ABC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG是菱形:
(2)若∠BAC=30°,BC=2,求四边形BDFG的面积.
【解答】(1)证明:∵∠ABC=90°,BD为AC的中线,
∴BD=AC,
∵AG∥BD,BD=FG,
∴四边形BDFG是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴DF=AC,
∴BD=DF;
∴平行四边形BDFG是菱形;
(2)解:作DH⊥AG于H,如图所示:
∵四边形BDFG是菱形,
∴GF=BD,
∵∠ABC=90°,∠BAC=30°,BC=2,
∴AC=2BC=4,
∵点D是AC中点,
∴GF=BD=AC=AD=2,
∴∠DBA=∠BAC=30°,
又∵AG∥BD,
∴∠BAF=∠DBA=30°,
∴∠DAF=60°,
∵DH⊥AG,
∴∠ADH=30°,
∴AH=AD=1,DH=AH=,
∴S菱形BDFG=GF?DH=2×=2.
24.(12分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)试探索OE与OF之间的数量关系.
(2)当点O运动到何处时,四边形AECF是矩形,并给出说理过程.
(3)在(2)的前提下,如果四边形AECF是正方形,那么△ABC将是什么三角形呢?请说明理由.
解:(1)∵MN∥BC,
∴∠OEC=∠ECB,∠OFC=∠FCD.
又∵CE平分∠ACB,FC平分∠ACD.
∴∠ECB=∠OCE,∠OCF=∠FCD,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴EO=OC,FO=OC,
∴EO=FO;
(2)由(1)知,OE=OC=OF,
当OC=OA,即点O为AC的中点时,
∴OE=OC=OF=OA,
∴四边形AECF是平行四边形,AC=EF,
∴这时四边形AECF是矩形;
∴当点O运动到AC中点时,
四边形AECF是矩形,
(3)由正方形AECF可知,AC⊥EF,
又∵EF∥BC,
∴∠ACB=90°,
∴△ABC是∠ACB=90°的直角三角形.
25.(12分)如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接DF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,求证:CE=PE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给予证明.
解:(1)延长EP交DC于点G,如图(1)所示:
∵∠FEC=∠DCE=90°,
∴EF∥CD,
∴∠PFE=∠PDG,
又∵∠EPF=∠GPD,PF=PD,
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,
∴BE=GD.
∵CD=CB,
∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=EG=PE,
∴△CPE是等腰直角三角形,
∴CE=PE;
(2)CE=PE,理由如下:
延长EP交CD的延长线于点G,如图(2)所示:
∵∠FEB+∠DCB=180°,
∴EF∥CD,
∴∠PEF=∠PGD,
又∵∠EPF=∠GPD,PF=PD,
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,
∴BE=GD.
∵CD=CB,
∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=EG=PE,
∴△CPE是等腰直角三角形,
∴CE=PE.
一、选择题(共12小题).
1.(3分)已知a﹣b=1,则a2﹣b2﹣2b的值为( )
A.4 B.3 C.1 D.0
2.(3分)若的值为,则的值为( )
A. B. C. D..
3.(3分)已知x1,x2,…xn的平均数为5,方差为2,则3x1﹣2,3x2﹣2…3xn﹣2的平均数和方差分别是( )
A.13和18 B.13和4 C.5和18 D.5和4
4.(3分)如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
A.110° B.80° C.40° D.30°
5.(3分)如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a﹣b)等于( )
A.4 B.5 C.6 D.7
6.(3分)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
7.(3分)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
8.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=_____,平行四边形CDEB为菱形.( )
A. B. C. D.3
9.(3分)如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A.(,﹣) B.(﹣,) C.(2,﹣2) D.(,﹣)
10.(3分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A.3 B.4 C. D.
11.(3分)如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
12.(3分)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6个小题,每小题3分,共18分,把答案填在题中的横线上.)
13.(3分)已知m2+=51,则|m﹣|= .
14.(3分)若分式方程=5+有增根,则a的值为 .
15.(3分)如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为 .
16.(3分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
17.(3分)如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转.在旋转过程中,当AE=BF时,∠AOE的大小是 .
18.(3分)如图,已知△ABC的面积是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2019个三角形的面积 .
三、解答题(本大题共7个小题,共66分,解答应写出文字说明、推理过程或演算步骤.)
19.(6分)先化简,再求值:(﹣)?,其中x=4.
20.(10分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
21.(8分)如图在△ABC中,以BC为边向三角形外做等边三角形△BCD,把△ABD绕D点按顺时针方向旋转60°后得到△ECD,且点A、C、E在同一条直线上,若AB=4,AC=2.
求:(1)∠ADE的度数;
(2)AD的长.
22.(8分)如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别交BC于点E,F,AE与DF相交于点G.
求证:(1)∠AGD=90°;
(2)BF=CE.
23.(10分)如图,在△ABC中,∠ABC=90°,BD为△ABC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG是菱形:
(2)若∠BAC=30°,BC=2,求四边形BDFG的面积.
24.(12分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)试探索OE与OF之间的数量关系.
(2)当点O运动到何处时,四边形AECF是矩形,并给出说理过程.
(3)在(2)的前提下,如果四边形AECF是正方形,那么△ABC将是什么三角形呢?请说明理由.
25.(12分)如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接DF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,求证:CE=PE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给予证明.
参考答案
一、选择题(本大题共12个小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求.)
1.(3分)已知a﹣b=1,则a2﹣b2﹣2b的值为( )
A.4 B.3 C.1 D.0
解:∵a﹣b=1,
∴a2﹣b2﹣2b=(a+b)(a﹣b)﹣2b
=a+b﹣2b
=a﹣b
=1.
故选:C.
2.(3分)若的值为,则的值为( )
A. B. C. D..
解:∵=,
∴2y2+3y=1,
∴原式===﹣.
故选:D.
3.(3分)已知x1,x2,…xn的平均数为5,方差为2,则3x1﹣2,3x2﹣2…3xn﹣2的平均数和方差分别是( )
A.13和18 B.13和4 C.5和18 D.5和4
解:∵x1,x2,…xn的平均数为5,
∴3x1﹣2,3x2﹣2…3xn﹣2的平均数是3×5﹣2=13,
∵x1,x2,…xn的方差为2,
∴3x1﹣2,3x2﹣2…3xn﹣2的方差是2×32=18.
故选:A.
4.(3分)如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
A.110° B.80° C.40° D.30°
解:根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,
∵∠A=40°,
∴∠A′=40°,
∵∠B′=110°,
∴∠A′CB′=180°﹣110°﹣40°=30°,
∴∠ACB=30°,
∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠ACA′=50°,
∴∠BCA′=30°+50°=80°,
故选:B.
5.(3分)如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a﹣b)等于( )
A.4 B.5 C.6 D.7
解:设重叠部分面积为c,
a﹣b=(a+c)﹣(b+c)=18﹣12=6,
故选:C.
6.(3分)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为( )
A.22 B.23 C.24 D.25
解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=9,CD=AB=6,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠AEB=∠BAE,
∴BE=AB=6,
∴CE=BC﹣BE=3,
∵BG⊥AE,
∴∠BGE=90°,AG=EG,
∴EG===2,
∴AE=2EG=4,
∴梯形AECD的周长=AE+CE+CD+AD=4+3+6+9=22,
故选:A.
7.(3分)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
解:∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB==5,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
8.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=_____,平行四边形CDEB为菱形.( )
A. B. C. D.3
解:如图,连接CE交AB于点O.
∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB===5.
若平行四边形CDEB为菱形时,CE⊥BD,且OD=OB,CD=CB.
∵S△ACB=AB?OC=AC?BC,
∴OC=.
∴在Rt△BOC中,根据勾股定理得,OB===,
∴AD=AB﹣2OB=.
故选:A.
9.(3分)如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A.(,﹣) B.(﹣,) C.(2,﹣2) D.(,﹣)
解:连接OB,OB′,过点B′作B′E⊥x轴于E,
根据题意得:∠BOB′=105°,
∵四边形OABC是菱形,
∴OA=AB,∠AOB=∠AOC=∠ABC=×120°=60°,
∴△OAB是等边三角形,
∴OB=OA=2,
∴∠AOB′=∠BOB′﹣∠AOB=105°﹣60°=45°,OB′=OB=2,
∴OE=B′E=OB′?sin45°=2×=,
∴点B′的坐标为:(,﹣).
故选:A.
10.(3分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
A.3 B.4 C. D.
解:∵CE=5,△CEF的周长为18,
∴CF+EF=18﹣5=13.
∵F为DE的中点,
∴DF=EF.
∵∠BCD=90°,
∴CF=DE,
∴EF=CF=DE=6.5,
∴DE=2EF=13,
∴CD=.
∵四边形ABCD是正方形,
∴BC=CD=12,O为BD的中点,
∴OF是△BDE的中位线,
∴OF=(BC﹣CE)=(12﹣5)=.
故选:D.
11.(3分)如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB?BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=×5×PE+×5×PF=(PE+PF)=12,
解得:PE+PF=4.8.
故选:A.
12.(3分)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
解:作F点关于BD的对称点F′,连接EF′交BD于点P,则PF=PF′.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=DF′=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故选:C.
二、填空题(本大题共6个小题,每小题3分,共18分,把答案填在题中的横线上.)
13.(3分)已知m2+=51,则|m﹣|= 7 .
解:∵m2+=51,
∴m2+﹣2=51﹣2,即(m﹣)2=49,
则|m﹣|=7,
故答案为:7.
14.(3分)若分式方程=5+有增根,则a的值为 4 .
解:去分母得:x=5x﹣20+a,
由分式方程有增根,得到x﹣4=0,即x=4,
把x=4代入整式方程得:4=20﹣20+a,
解得:a=4,
故答案为:4.
15.(3分)如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为 7 .
解:由折叠的性质可得EF=AE、BF=AB,
∴?ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=8+22=30,
∵四边形ABCD为平行四边形,
∴AB+BC=15,
∵△FCB的周长=CF+BC+BF=CF+BC+AB=22,
即FC+15=22,
∴FC=7,
故答案为7.
16.(3分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
解:连接BD交AC于O,
∵四边形ABCD、AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG,
∴∠EAB=∠GAD,
在△AEB和△AGD中,
,
∴△EAB≌△GAD(SAS),
∴EB=GD,
∵四边形ABCD是正方形,AB=,
∴BD⊥AC,AC=BD=AB=2,
∴∠DOG=90°,OA=OD=BD=1,
∵AG=1,
∴OG=OA+AG=2,
∴GD==,
∴EB=.
故答案为:.
17.(3分)如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转.在旋转过程中,当AE=BF时,∠AOE的大小是 15°或165° .
解:连结AE、BF,
如图1,
∵四边形ABCD为正方形,
∴OA=OB,∠AOB=90°,
∵△OEF为等边三角形,
∴OE=OF,∠EOF=60°,
∵在△OAE和△OBF中
,
∴△OAE≌△OBF(SSS),
∴∠AOE=∠BOF=(90°﹣60°)=15°,
如图2,
∵在△AOE和△BOF中
,
∴△AOE≌△BOF(SSS),
∴∠AOE=∠BOF,
∴∠DOF=∠COE,
∴∠DOF=(90°﹣60°)=15°,
若F点在E点上方,则∠AOE=180°﹣15°=165°;
∴∠AOE大小为15°或165°.
故答案为15°或165°.
18.(3分)如图,已知△ABC的面积是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2019个三角形的面积 ()2018 .
解:∵D、E、F分别为AB、BC、AC的中点,
∴DE、EF、DF分别为△ABC的中位线,
∴DE=AC,DF=BC,EF=AB,
作AG⊥DE于G,交BC于H,则AG=GH,
∵△ABC的面积=BC×AH,△DEF的面积=DE×GH,
∴△DEF的面积=△ABC的面积=,
同理:第三个三角形的面积=△DEF的面积==()2,第四个三角形的面积=第三个三角形面积=()3,……,
∴第2019个三角形的面积为()2018,
故答案为:()2018.
三、解答题(本大题共7个小题,共66分,解答应写出文字说明、推理过程或演算步骤.)
19.(6分)先化简,再求值:(﹣)?,其中x=4.
解:原式=?
=x+2,
当x=4时,原式=6.
20.(10分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,
由题意,得=2×+300,
解得x=5,
经检验x=5是原方程的解.
答:该种干果的第一次进价是每千克5元;
(2)[+﹣600]×9+600×9×80%﹣(3000+9000)
=(600+1500﹣600)×9+4320﹣12000
=1500×9+4320﹣12000
=13500+4320﹣12000
=5820(元).
答:超市销售这种干果共盈利5820元.
21.(8分)如图在△ABC中,以BC为边向三角形外做等边三角形△BCD,把△ABD绕D点按顺时针方向旋转60°后得到△ECD,且点A、C、E在同一条直线上,若AB=4,AC=2.
求:(1)∠ADE的度数;
(2)AD的长.
解:(1)△ABD绕D点按顺时针方向旋转60°后得到△ECD,
∴∠ADE=60°.
(2)△ABD绕D点按顺时针方向旋转60°后得到△ECD,
∴∠ADE=60°,AD=DE,
∴△AED为等边三角形,
又∵CE=BA=4,AC=2,
∴AE=6,
∴AD=6.
22.(8分)如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别交BC于点E,F,AE与DF相交于点G.
求证:(1)∠AGD=90°;
(2)BF=CE.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴∠BAD+∠ADC=180°.
∵AE,DF分别平分∠BAD,∠ADC,
∴∠DAG=∠BAD,∠ADG=∠ADC.
∴∠DAG+∠ADG=×180°=90°.
∴∠AGD=180°﹣90°=90°.
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
同理DC=CF,
又∵AB=CD,
∴BE=CF,
∴BF=CE.
23.(10分)如图,在△ABC中,∠ABC=90°,BD为△ABC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG是菱形:
(2)若∠BAC=30°,BC=2,求四边形BDFG的面积.
【解答】(1)证明:∵∠ABC=90°,BD为AC的中线,
∴BD=AC,
∵AG∥BD,BD=FG,
∴四边形BDFG是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴DF=AC,
∴BD=DF;
∴平行四边形BDFG是菱形;
(2)解:作DH⊥AG于H,如图所示:
∵四边形BDFG是菱形,
∴GF=BD,
∵∠ABC=90°,∠BAC=30°,BC=2,
∴AC=2BC=4,
∵点D是AC中点,
∴GF=BD=AC=AD=2,
∴∠DBA=∠BAC=30°,
又∵AG∥BD,
∴∠BAF=∠DBA=30°,
∴∠DAF=60°,
∵DH⊥AG,
∴∠ADH=30°,
∴AH=AD=1,DH=AH=,
∴S菱形BDFG=GF?DH=2×=2.
24.(12分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)试探索OE与OF之间的数量关系.
(2)当点O运动到何处时,四边形AECF是矩形,并给出说理过程.
(3)在(2)的前提下,如果四边形AECF是正方形,那么△ABC将是什么三角形呢?请说明理由.
解:(1)∵MN∥BC,
∴∠OEC=∠ECB,∠OFC=∠FCD.
又∵CE平分∠ACB,FC平分∠ACD.
∴∠ECB=∠OCE,∠OCF=∠FCD,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴EO=OC,FO=OC,
∴EO=FO;
(2)由(1)知,OE=OC=OF,
当OC=OA,即点O为AC的中点时,
∴OE=OC=OF=OA,
∴四边形AECF是平行四边形,AC=EF,
∴这时四边形AECF是矩形;
∴当点O运动到AC中点时,
四边形AECF是矩形,
(3)由正方形AECF可知,AC⊥EF,
又∵EF∥BC,
∴∠ACB=90°,
∴△ABC是∠ACB=90°的直角三角形.
25.(12分)如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接DF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,求证:CE=PE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给予证明.
解:(1)延长EP交DC于点G,如图(1)所示:
∵∠FEC=∠DCE=90°,
∴EF∥CD,
∴∠PFE=∠PDG,
又∵∠EPF=∠GPD,PF=PD,
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,
∴BE=GD.
∵CD=CB,
∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=EG=PE,
∴△CPE是等腰直角三角形,
∴CE=PE;
(2)CE=PE,理由如下:
延长EP交CD的延长线于点G,如图(2)所示:
∵∠FEB+∠DCB=180°,
∴EF∥CD,
∴∠PEF=∠PGD,
又∵∠EPF=∠GPD,PF=PD,
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,
∴BE=GD.
∵CD=CB,
∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=EG=PE,
∴△CPE是等腰直角三角形,
∴CE=PE.
同课章节目录
