函数的概念
图片预览






文档简介
(共20张PPT)
量:具体表达事物的某些特征
数:表明量的大小
数与度量单位合在一起,就是“数量”
例如,我们居住的地球,可以用下列数量 来描述它的一些特征:
表面积 510×106平方千米
体积 1083×109立方千米
质量 598×1019吨
绕太阳运行的平均速度 29.77千米/秒
平均半径 6371.22千米
在问题研究的过程中,可以取不同数值的量叫做变量
保持数值不变的量叫做常量(或常数)
一个成年人,在一天当中,
是早晨高还是晚上高呢?
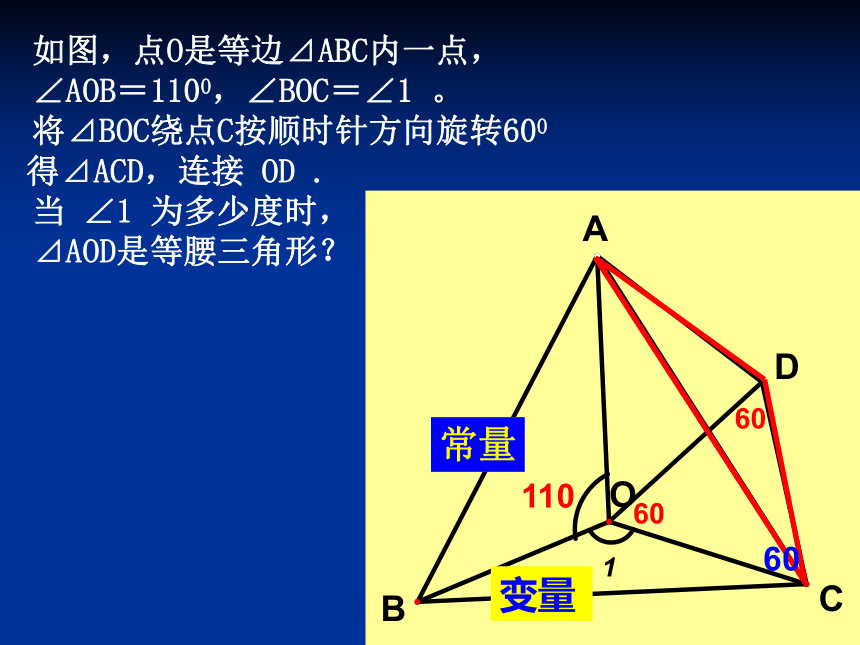
如图,点O是等边⊿ABC内一点,
∠AOB=1100,∠BOC=∠1 。
将⊿BOC绕点C按顺时针方向旋转600
得⊿ACD,连接 OD .
当 ∠1 为多少度时,
⊿AOD是等腰三角形?
110
60
变量
60
常量
60
矩形的面积等于长乘宽S=ab
⑴若a=10,则a是 量,S,b是 量;
⑵若b=5, 则b是 量,S,a是 量;
⑶若S=80,则S是 量,a,b是 量;
常量与变量不是绝对的,而是相对于一个变化过程而言的.
启发:
常
变
常
变
常
变
填一填
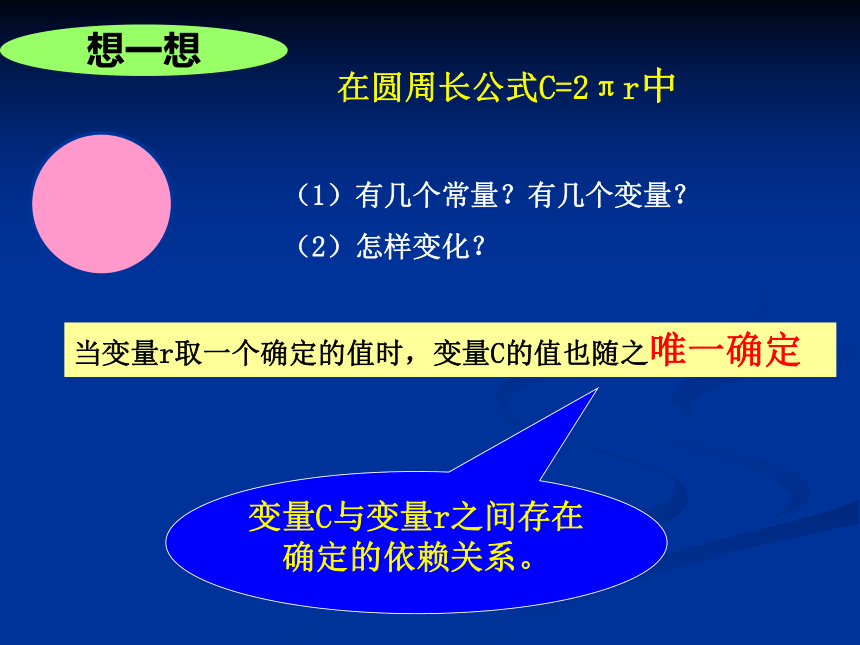
在圆周长公式C=2πr中
(1)有几个常量?有几个变量?
(2)怎样变化?
当变量r取一个确定的值时,变量C的值也随之唯一确定
变量C与变量r之间存在
确定的依赖关系。
想一想
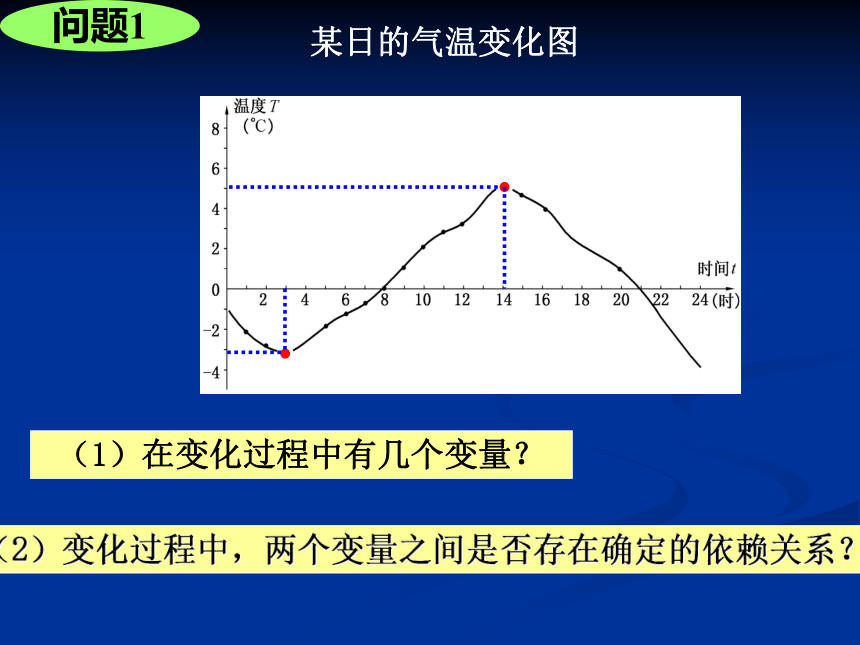
某日的气温变化图
(1)在变化过程中有几个变量?
(2)变化过程中,两个变量之间是否存在确定的依赖关系?
问题1
y=120-0.2x 。当x取一个确定数值时,y的值也唯一确定,所以y与x之间存在确定的依赖关系.
一辆汽车行驶在国道上,汽车油箱里原有
汽油120升,每行驶10千米耗油2升。
(1)填表
汽车行驶的路程
x(千米) 100km 150km 200km 250km
油箱里剩余的油量y(升)
100升
90升
80升
70升
问题2
(0≤x≤600)
这两个问题有什么共同之处?
(1)一个变化过程,
(2)两个变量,
(3)两个变量之间存在确定的依赖关系。
汽车行驶的
路程 100km 150km 200km 250km
油箱里剩余 油量 100升 90升 80升 70升
问题1
问题2
y=120-0.2x
(0≤x≤600)
函数三要素
看一看
如果在变量x的允许取值范围内,变量y随着x的变化
而变化,
谈一谈
在某个变化过程中有两个变量,设为x和y,
它们之间存在确定的依赖关系,
那么变量y叫做变量x的函数,
x叫做自变量
在问题2中,变量y是变量x的函数,x是自变量,其中y随着x变化而变化的依赖关系,是由“y=120-0.2x”表达出来的。
这种表达两个变量之间依赖关系的数学式子称为函数解析式。
C=2πr
如图,点O是等边⊿ABC内一点,
∠AOB=1100,∠BOC=∠1 。
将⊿BOC绕点C按顺时针方向旋转600
得⊿ACD,连接 OD .
当 ∠1 为多少度时,
⊿AOD是等腰三角形?
110
60
60
x
190-x
X-60
图像法
y=120-0.2x
请说说函数有那些表示方法?
列表法
解析法
问题1
问题2
问题2
说一说
汽车行驶的
路程 100km 150km 200km 250km
油箱里剩余的
油量 100升 90升 80升 70升
德国著名心理学家艾宾浩斯(1850——1909年)对人的记忆进行了研究,他采用无意义的音节作为记忆的材料进行实验,获得了如下相关数据:
时间 刚记忆完 20分钟后 1小时后 9小时后 1天后 2天后 6天后 30天后
记忆量 100% 58.2% 44.2% 35.8% 32.7% 27.8% 25.4% 21.1%
他又根据上表绘制了一条曲线,这就是著名的艾宾浩斯保持曲线
观察这条曲线,回答:
在这一变化过程中,有哪两个变量?他们之间是否存在确定的依赖关系?其中一个变量是另一个变量的函数吗?为什么?
练一练
问题1 下图是某地一天内的气温变化图
(1)这天的6时、10时和14时的气温分别为多少?
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?
什么时段的气温在逐渐降低?
(4)任选时刻t的一个值,温度T有几个值和这个时刻对应
练一练
问题1
如果x是一个变量,那么x+2也是一个变量。
试问:变量x+2是不是变量x的函数?
议一议
常量
变量
函数
自变量
函数解析式
相对性
一个变化过程
两个变量
两个变量之间存在确定的依赖关系
五
个
概
念
相对性
解析法
图像法
列表法
函数的三种表达法
小结
2.某地民用电的单价是每度0.5元,设使用x度电应付电
费y元,则y与x的关系式是 ;在这个变化
过程中 是变量, 是常量.
3.火车行驶2000千米的路程,用v(千米/时)表示行驶
的速度,t(时)表示所需的时间,其中常量是____,
变量是_____,t与v之间的关系式是______.
1.在圆周长公式S=πR2中,变量的个数是( )
(A)1 (B)2 (C)3 (D)4
B
x、y
y=0.5x
2000
0.5
v、t
练一练
思考
如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与D不重合),分别联结CA、CB,得到△ABC.
(1)指出△ABC的面积的变化过程中,线段AB、CD的长哪个是常量?哪个是变量? (2)设CD的长为h,△ABC 的面积为S,S是不是h的函数?
A
D
B
C
E
小明为了表示爷爷吃过晚饭后,出门散步、报亭看报、回家的过程,绘制了爷爷离家的路程s与外出时间之间的关系图,请根据这个关系图回答下列问题.
(1)这个关系图反映了哪几个变量之间的关系
(2)任取变量t的一个值,变量S有几个值与它对应,
变量s是t的函数吗
(3)报亭离爷爷家有多远 爷爷在报亭
看了多长时间的报
(4)爷爷出门,返回的平均速度
分别是多少
0
400
t(分)
S(米)
40
25
10
思考
量:具体表达事物的某些特征
数:表明量的大小
数与度量单位合在一起,就是“数量”
例如,我们居住的地球,可以用下列数量 来描述它的一些特征:
表面积 510×106平方千米
体积 1083×109立方千米
质量 598×1019吨
绕太阳运行的平均速度 29.77千米/秒
平均半径 6371.22千米
在问题研究的过程中,可以取不同数值的量叫做变量
保持数值不变的量叫做常量(或常数)
一个成年人,在一天当中,
是早晨高还是晚上高呢?
如图,点O是等边⊿ABC内一点,
∠AOB=1100,∠BOC=∠1 。
将⊿BOC绕点C按顺时针方向旋转600
得⊿ACD,连接 OD .
当 ∠1 为多少度时,
⊿AOD是等腰三角形?
110
60
变量
60
常量
60
矩形的面积等于长乘宽S=ab
⑴若a=10,则a是 量,S,b是 量;
⑵若b=5, 则b是 量,S,a是 量;
⑶若S=80,则S是 量,a,b是 量;
常量与变量不是绝对的,而是相对于一个变化过程而言的.
启发:
常
变
常
变
常
变
填一填
在圆周长公式C=2πr中
(1)有几个常量?有几个变量?
(2)怎样变化?
当变量r取一个确定的值时,变量C的值也随之唯一确定
变量C与变量r之间存在
确定的依赖关系。
想一想
某日的气温变化图
(1)在变化过程中有几个变量?
(2)变化过程中,两个变量之间是否存在确定的依赖关系?
问题1
y=120-0.2x 。当x取一个确定数值时,y的值也唯一确定,所以y与x之间存在确定的依赖关系.
一辆汽车行驶在国道上,汽车油箱里原有
汽油120升,每行驶10千米耗油2升。
(1)填表
汽车行驶的路程
x(千米) 100km 150km 200km 250km
油箱里剩余的油量y(升)
100升
90升
80升
70升
问题2
(0≤x≤600)
这两个问题有什么共同之处?
(1)一个变化过程,
(2)两个变量,
(3)两个变量之间存在确定的依赖关系。
汽车行驶的
路程 100km 150km 200km 250km
油箱里剩余 油量 100升 90升 80升 70升
问题1
问题2
y=120-0.2x
(0≤x≤600)
函数三要素
看一看
如果在变量x的允许取值范围内,变量y随着x的变化
而变化,
谈一谈
在某个变化过程中有两个变量,设为x和y,
它们之间存在确定的依赖关系,
那么变量y叫做变量x的函数,
x叫做自变量
在问题2中,变量y是变量x的函数,x是自变量,其中y随着x变化而变化的依赖关系,是由“y=120-0.2x”表达出来的。
这种表达两个变量之间依赖关系的数学式子称为函数解析式。
C=2πr
如图,点O是等边⊿ABC内一点,
∠AOB=1100,∠BOC=∠1 。
将⊿BOC绕点C按顺时针方向旋转600
得⊿ACD,连接 OD .
当 ∠1 为多少度时,
⊿AOD是等腰三角形?
110
60
60
x
190-x
X-60
图像法
y=120-0.2x
请说说函数有那些表示方法?
列表法
解析法
问题1
问题2
问题2
说一说
汽车行驶的
路程 100km 150km 200km 250km
油箱里剩余的
油量 100升 90升 80升 70升
德国著名心理学家艾宾浩斯(1850——1909年)对人的记忆进行了研究,他采用无意义的音节作为记忆的材料进行实验,获得了如下相关数据:
时间 刚记忆完 20分钟后 1小时后 9小时后 1天后 2天后 6天后 30天后
记忆量 100% 58.2% 44.2% 35.8% 32.7% 27.8% 25.4% 21.1%
他又根据上表绘制了一条曲线,这就是著名的艾宾浩斯保持曲线
观察这条曲线,回答:
在这一变化过程中,有哪两个变量?他们之间是否存在确定的依赖关系?其中一个变量是另一个变量的函数吗?为什么?
练一练
问题1 下图是某地一天内的气温变化图
(1)这天的6时、10时和14时的气温分别为多少?
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?
什么时段的气温在逐渐降低?
(4)任选时刻t的一个值,温度T有几个值和这个时刻对应
练一练
问题1
如果x是一个变量,那么x+2也是一个变量。
试问:变量x+2是不是变量x的函数?
议一议
常量
变量
函数
自变量
函数解析式
相对性
一个变化过程
两个变量
两个变量之间存在确定的依赖关系
五
个
概
念
相对性
解析法
图像法
列表法
函数的三种表达法
小结
2.某地民用电的单价是每度0.5元,设使用x度电应付电
费y元,则y与x的关系式是 ;在这个变化
过程中 是变量, 是常量.
3.火车行驶2000千米的路程,用v(千米/时)表示行驶
的速度,t(时)表示所需的时间,其中常量是____,
变量是_____,t与v之间的关系式是______.
1.在圆周长公式S=πR2中,变量的个数是( )
(A)1 (B)2 (C)3 (D)4
B
x、y
y=0.5x
2000
0.5
v、t
练一练
思考
如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与D不重合),分别联结CA、CB,得到△ABC.
(1)指出△ABC的面积的变化过程中,线段AB、CD的长哪个是常量?哪个是变量? (2)设CD的长为h,△ABC 的面积为S,S是不是h的函数?
A
D
B
C
E
小明为了表示爷爷吃过晚饭后,出门散步、报亭看报、回家的过程,绘制了爷爷离家的路程s与外出时间之间的关系图,请根据这个关系图回答下列问题.
(1)这个关系图反映了哪几个变量之间的关系
(2)任取变量t的一个值,变量S有几个值与它对应,
变量s是t的函数吗
(3)报亭离爷爷家有多远 爷爷在报亭
看了多长时间的报
(4)爷爷出门,返回的平均速度
分别是多少
0
400
t(分)
S(米)
40
25
10
思考
