14.2命题与证明
图片预览





文档简介
(共15张PPT)
14.2 命题与证明
第一课时 命题
(1)多可爱的804班学生啊!
(2)你们欢迎我吗?
(3)2008年奥运会是在桐城市举办的。
(4)1+2>3 。
(5)0.5是整数。
(6)对顶角相等。
(7)连结A、B两点。
(8)若x2=1,则x=1 。
思 考
下列各语句中,哪些是作出判断的句子,哪些不是?
命题的概念
可以判断它是真(正确)、假(错误)的语句或式子叫做命题。
(1)多可爱的804班学生啊!
(2)你们欢迎我吗?
(3)2008年奥运会是在桐城市举办的。
(4)1+2>3 。 (5)0.5是整数。
(6)对顶角相等。 (7)连结A、B两点。
(8)若x2=1,则x=1 。
反之,若一个语句没有对某一事件的正确与否作出任何判断,则它不是命题。
(1)今天天气如何?
(2)你是不是作业没交?
(3)这里景色多美啊!
(4)-2不是整数。
(5)4>3。
看看下列语句是不是命题?
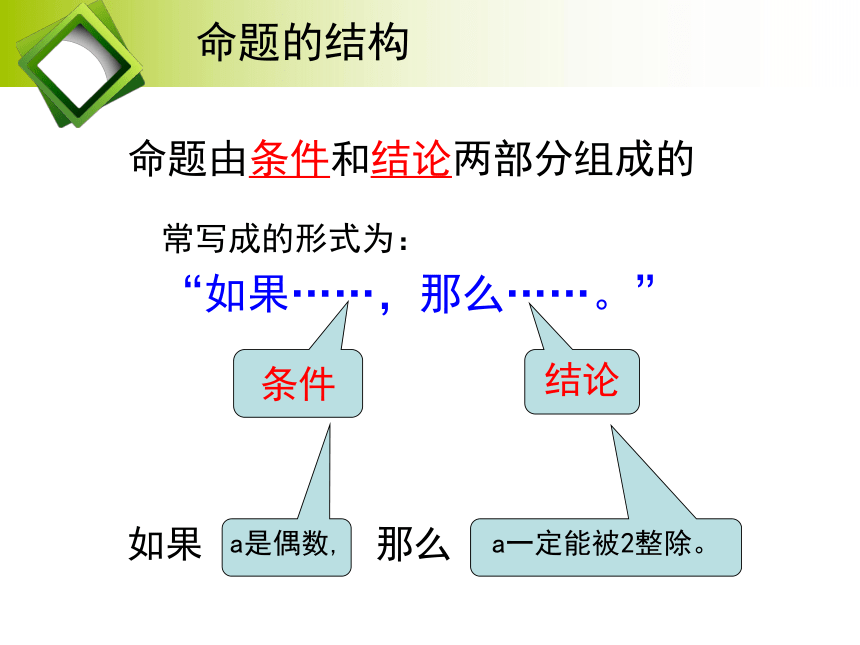
命题由条件和结论两部分组成的
常写成的形式为:
“如果……,那么……。”
条件
结论
如果 那么
a是偶数,
a一定能被2整除。
命题的结构
命题结构的深析
对于一些条件与结论不明显的命题,一般采取先添补一些命题中省略的词句,写成“如果……,那么……。”的形式后,再确定条件与结论。
如命题:a>0时,函数y=ax+b的值随x的增加而增加。
写成“如果……, 那么……。”的形式为:
a>0时,如果x增加,那么函数y=ax+b的值随之增加。
或:当x增加时,如果a>0,那么函数y=ax+b的值也增加。
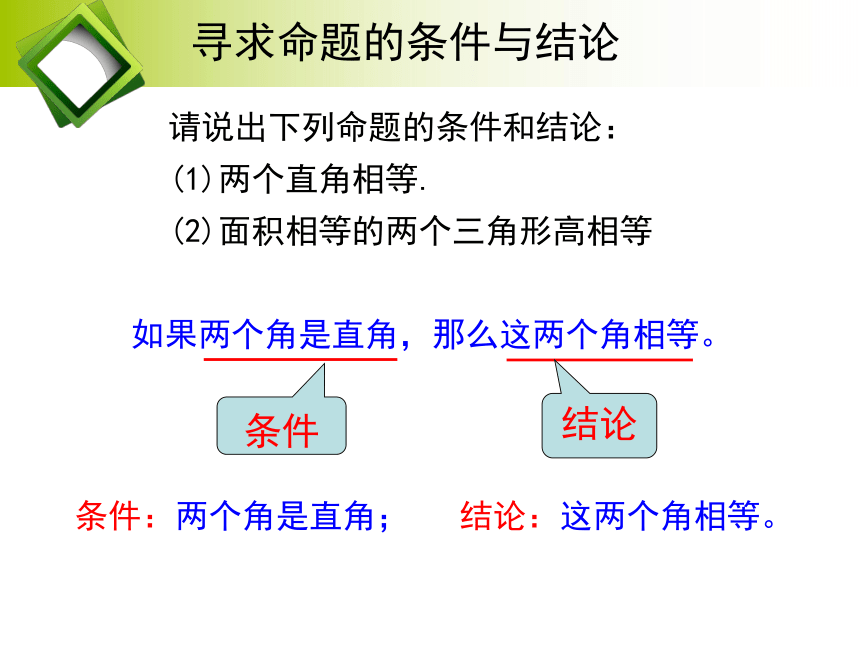
请说出下列命题的条件和结论:
(1)两个直角相等.
(2)面积相等的两个三角形高相等
如果两个角是直角,那么这两个角相等。
条件
结论
条件:两个角是直角; 结论:这两个角相等。
寻求命题的条件与结论
正确的命题叫做真命题;
错误的命题叫做假命题。
假命题
假命题
假命题
真命题
假命题
假命题
真命题与假命题
判断下列命题是真命题还是假命题:
(1)2008年奥运会是在桐城市举办的。
(2)1+2>3 。
(3)0.5是整数。
(4)对顶角相等。
(5)若x2=1,则x=1 。
(6)一个锐角与一个钝角的和等于180°。
“一个锐角与一个钝角的和等于180°。”
因为 30°是锐角,120°是钝角,
而 30°+ 120°=150°≠180 °,
所以“一个锐角与一个钝角的和等于180°”是假命题。
如上:判断一个命题是假命题,只要举出一个符合命题条件,但不满足命题结论的例子就可以了。像这样的例子叫做反例。
假命题:
反 例
原命题与逆命题
命题“若a是偶数,则a一定能被2整除。”
具有“若p则q”的形式。
(其中p 是这个命题的条件,q是这个命题的结论。)
q
p
命题“若p则q”与命题“若q则p” 这样两个命题(条件与结论互换)称为互逆命题。
其中一个叫做原命题,
则另一个就叫做原命题的逆命题。
互逆命题的真假性
注意:当原命题是真命题时,它所对应的逆命题不一定为真命题。即原命题的真假与其逆命题的真假无关。
请同学们举两个例子让我们一起感受下!
这节课你有何收获,
能与大家分享、交流你的感受吗?
作业布置
教材85页
习题1,2,3
课后思考题
1.对于同一平面内三条直线a, b, c,给出下列五个选项:
1. a ∥ b 2. b ∥ c
3. a ⊥ b 4. a ∥ c
5. a ⊥ c
以其中两个为条件,一个为结论,组成一个你认为正确的命题 。
2.“X>6”是不是命题?
14.2 命题与证明
第一课时 命题
(1)多可爱的804班学生啊!
(2)你们欢迎我吗?
(3)2008年奥运会是在桐城市举办的。
(4)1+2>3 。
(5)0.5是整数。
(6)对顶角相等。
(7)连结A、B两点。
(8)若x2=1,则x=1 。
思 考
下列各语句中,哪些是作出判断的句子,哪些不是?
命题的概念
可以判断它是真(正确)、假(错误)的语句或式子叫做命题。
(1)多可爱的804班学生啊!
(2)你们欢迎我吗?
(3)2008年奥运会是在桐城市举办的。
(4)1+2>3 。 (5)0.5是整数。
(6)对顶角相等。 (7)连结A、B两点。
(8)若x2=1,则x=1 。
反之,若一个语句没有对某一事件的正确与否作出任何判断,则它不是命题。
(1)今天天气如何?
(2)你是不是作业没交?
(3)这里景色多美啊!
(4)-2不是整数。
(5)4>3。
看看下列语句是不是命题?
命题由条件和结论两部分组成的
常写成的形式为:
“如果……,那么……。”
条件
结论
如果 那么
a是偶数,
a一定能被2整除。
命题的结构
命题结构的深析
对于一些条件与结论不明显的命题,一般采取先添补一些命题中省略的词句,写成“如果……,那么……。”的形式后,再确定条件与结论。
如命题:a>0时,函数y=ax+b的值随x的增加而增加。
写成“如果……, 那么……。”的形式为:
a>0时,如果x增加,那么函数y=ax+b的值随之增加。
或:当x增加时,如果a>0,那么函数y=ax+b的值也增加。
请说出下列命题的条件和结论:
(1)两个直角相等.
(2)面积相等的两个三角形高相等
如果两个角是直角,那么这两个角相等。
条件
结论
条件:两个角是直角; 结论:这两个角相等。
寻求命题的条件与结论
正确的命题叫做真命题;
错误的命题叫做假命题。
假命题
假命题
假命题
真命题
假命题
假命题
真命题与假命题
判断下列命题是真命题还是假命题:
(1)2008年奥运会是在桐城市举办的。
(2)1+2>3 。
(3)0.5是整数。
(4)对顶角相等。
(5)若x2=1,则x=1 。
(6)一个锐角与一个钝角的和等于180°。
“一个锐角与一个钝角的和等于180°。”
因为 30°是锐角,120°是钝角,
而 30°+ 120°=150°≠180 °,
所以“一个锐角与一个钝角的和等于180°”是假命题。
如上:判断一个命题是假命题,只要举出一个符合命题条件,但不满足命题结论的例子就可以了。像这样的例子叫做反例。
假命题:
反 例
原命题与逆命题
命题“若a是偶数,则a一定能被2整除。”
具有“若p则q”的形式。
(其中p 是这个命题的条件,q是这个命题的结论。)
q
p
命题“若p则q”与命题“若q则p” 这样两个命题(条件与结论互换)称为互逆命题。
其中一个叫做原命题,
则另一个就叫做原命题的逆命题。
互逆命题的真假性
注意:当原命题是真命题时,它所对应的逆命题不一定为真命题。即原命题的真假与其逆命题的真假无关。
请同学们举两个例子让我们一起感受下!
这节课你有何收获,
能与大家分享、交流你的感受吗?
作业布置
教材85页
习题1,2,3
课后思考题
1.对于同一平面内三条直线a, b, c,给出下列五个选项:
1. a ∥ b 2. b ∥ c
3. a ⊥ b 4. a ∥ c
5. a ⊥ c
以其中两个为条件,一个为结论,组成一个你认为正确的命题 。
2.“X>6”是不是命题?
