解一元一次方程---去括号

(共12张PPT)
一元一次方程的解法
----去括号
执教老师：李贤武
解下列方程，并口算检验
（1）10 x -3＝7 x +3
（2）8-5 x ＝ x ＋2
解：移项，得
合并同类项，得
系数化成１，得
解：移项，得
合并同类项，得
系数化成１，得
10 x -7 x ＝ 3 +3
3 x ＝ 6
x ＝ 2
-5x-x ＝＋2-8
-6x＝-6
x ＝ 1
想一想,做一做
同学们还记得如何去括号嘛？请将下面式子的括号去掉：
①+(2a-3b+c)
②2(x+2y-2)
③-(4a+3b-4c)
④-3(x-y-1)
＝2a-3b+c
＝2x＋4y－4
＝－4a－3b＋4c
＝－3x＋3y＋3
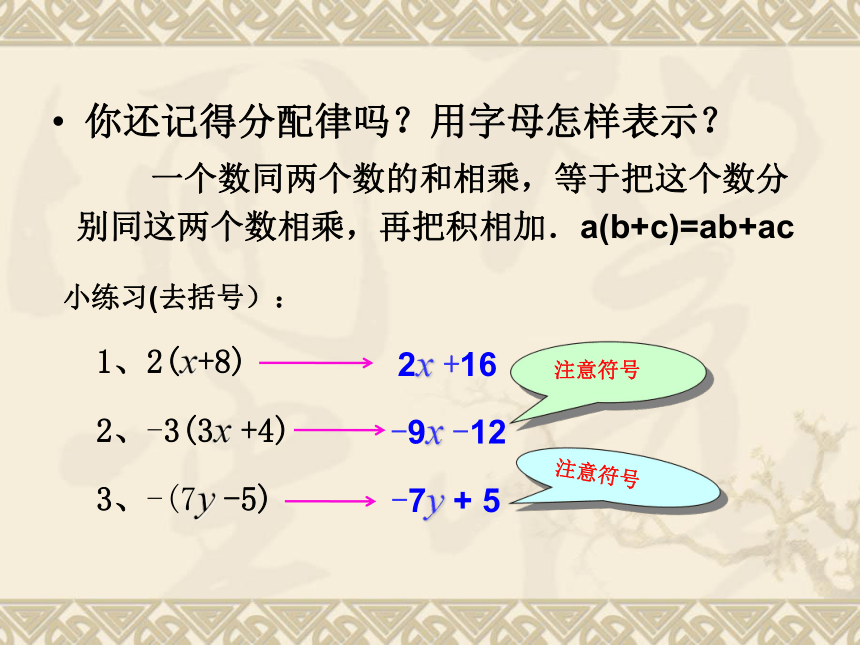
你还记得分配律吗？用字母怎样表示？
一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加．a(b+c)=ab+ac
小练习(去括号）：
1、2(x+8)
2、-3(3x +4)
3、-(7y -5)
2x +16
-9x -12
-7y + 5
注意符号
注意符号
（1）3-（4x-3）＝7 （2）3x -7(x -1)=3-2(x+3)
解：去括号，得
3x -7x+7=3-2x-6
移项，得
3x-7x+2x=3-6-7
合并同类项，得
-2x=-10
系数化成１，得
x=5
解：去括号，得
移项，得
合并同类项，得
系数化成１，得
例1：解方程
★去括号、移项、合并同类项、系数为化1时要注意的几个问题：
③ 合并同类项时，只是把同类项的系数相加作为所得项的系数，字母部分不变。
④系数化为1，要方程两边同时除以未知数前面的系数。
②移项要变号。
①去括号要注意括号外的正、负符号。
练习
1. 解下列方程：
（1）4x + 3（2x – 3）=12 – （x +4）
（2）6（ x– 4）+ 2 x =7 – （ x – 1）
1
2
1
3
2.如果关于m的方程2 m + b = m -1的解是-4，则b的值是( )
A. 3 B. 5 C . -3 D. -5
思考：结合今天所学内容，解一元一次方程的步骤是什么？
（4）系数化成１
（1）去括号
（2）移项
（3）合并同类项
（去括号法则）
（等式性质1）
（合并同类项法则）
（等式性质2）
它们分别运用了那些知识点？
作业布置：
P90　练习 2
P90－90　一元一次方程的解法
----去括号
布置作业：
1、作业本
2、课后练习
3、每课必练
5.2 一元一次方程的解法(1)
新课教学
例题练习
拓展应用
课的导入
我 学 习 我 快 乐
　移项，得：
方程两边同除以- 3，得：
解法一：去括号，得： - 3x－3=9
- 3x=9＋3
x= - 4
解法二：
　移项，得：
即：
方程两边同除以- 3，得：
x＋1=－3
x= - 3－1
x= - 4
化简，得：
- 3x=12
此方程可以先去括号,也可以当做为(x - 1)的一元一次方程进行求解.
思考题：　解方程： - 3(x＋1)=9
议一议：观察上述两种解法，说出它们的区别？
你能用几种方法来解此方程？试试