16.2线段的垂直平分线第一课时-冀教版八年级数学上册课件(共19张ppt)
文档属性
| 名称 | 16.2线段的垂直平分线第一课时-冀教版八年级数学上册课件(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 20:41:06 | ||
图片预览






文档简介
16.2 线段的垂直平分线(1)
第十六章 轴对称和中心对称
冀教版八上
学 习 目 标
1.会进行线段垂直平分线的性质定理的证明.
2.理解并能灵活运用线段垂直平分线的性质.
3.会作最短路径的问题.
冀教版八上
新课学习
B
A
O
P
M
N
如图,直线MN垂直平分线段AB,点P为MN上一点,连接PA,PB,你认为PA与PB之间具有什么关系?你能证明吗?
问题:
∵线段AB是轴对称图形,中垂线是其对称轴
∴当AB沿对称轴对折后,点A,B重合.
①用对称的知识说明:
B
A
O
P
M
N
新课学习
证明:∵MN ⊥ AB(已知)
∴∠AOP=∠BOP=90(垂直定义)
在△AOP与△ BOP中
∵ AO=BO(已知)
∠AOP=∠BOP(已证)
PO=PO(公共边)
∴ △ AOP≌ △ BOP(SAS)
∴ PA=PB(全等三角形对应边相等)
②用全等的知识进行推理:
B
A
O
P
M
N
新课学习
请用语言描述你证明出的结论:
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段的两端点的距离是相等的.
新课学习
新课学习
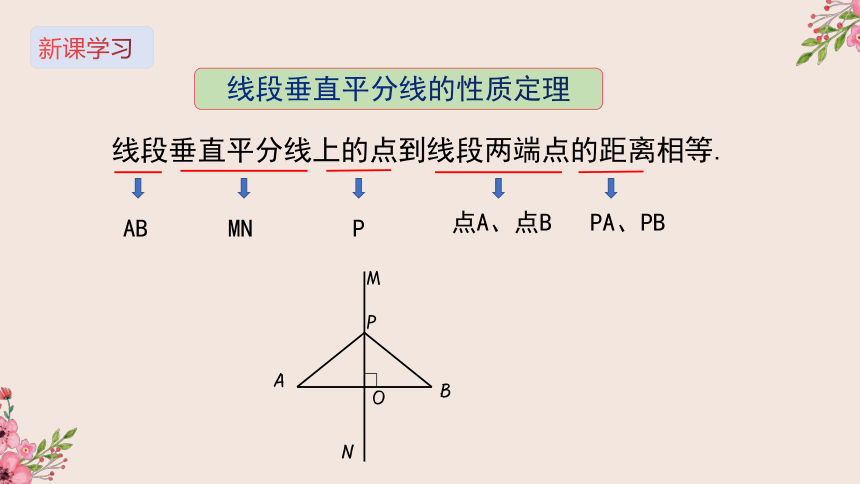
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两端点的距离相等.
B
A
O
P
M
N
AB
MN
P
点A、点B
PA、PB
新课学习
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两端点的距离相等.
几何语言:
∵MN垂直平分AB.
∴PA=PB.
用途:
推出相等的线段.
B
A
O
P
M
N
巩固练习
1.如图1所示,直线CD是线段PB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
P
A
B
C
D
2.如图2所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
图1
A
B
C
D
E
图2
B
10cm
典例精析
例题. 已知:如图,点A,B是直线l外任意两点,在直线l上,试确定一点P,使得AP+BP最短.
l
A
B
解:作点A关于直线l的对称点A',连接A'B ,交直线l于点P,则AP+BP最短.
A'
P
思考:
哪个知识点可以用来说明距离最短的问题?
两点之间线段最短.
典例精析
l
A
B
A'
P
由作图可知,l是AA'的中垂线
在l上另取一点M,连接MA,MB,MA'
∴AP=A'P,AM=A'M
∴AP+BP=A'P+BP=A'B
AM+BM=A'M+BM
由“两点之间线段最短”可得A'B<A'M+BM
即AP+BP最短
证明:
M
巩固练习
1.如图,A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边的什么地方,可使所修的渠道最短?
2.连接A'B,交a于点P.
作法:1.做点A关于a的对称点A'.
点P即为抽水站的位置.
A
B
a
A'
P
巩固练习
2.如图,点D在BC上,DE垂直平分AC,垂足为E,DF垂直平分BA,垂足为F,求证:DB=DC.
F
E
D
C
B
A
证明:连接AD
∵DE垂直平分AC
∴DA=DC
同理,DA=DB
∴DB=DC
课堂小测
A.AM>CN B.AM=CN C.AM<CN D.无法确定
1.如图,已知线段AB,BC的中垂线 交于点M,则线段AM,CM的大小关系是( )
B
A
C
M
B
课堂小测
2.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( ).
A.AB=AD B.AC平分∠BCD C.AB=BD D.△BEC≌△DEC
B
A
D
C
E
C
课堂小测
3.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠AOC=120°,则∠ABC= _____.
B
A
D
C
O
60°
课堂小测
4.如图,在△ABC中,AB=AC,D是AB的中点,且DE⊥AB,已知△BCD的周长为12,且AC-BC=2,求AC,BC的长.
A
B
C
D
E
解:∵D是AB的中点,DE⊥AB.
∴DE为AB的中垂线.
∴AE=BE.
∵△BCE的周长为12.
∴BC+CE+BE=12.
∴AC+BC=12.
∵AC-BC=2.
∴AC=7,BC=5.
课堂小结
线段的垂直平分的性质定理
性质
内容
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
实际运用
同学们再见
第十六章 轴对称和中心对称
冀教版八上
学 习 目 标
1.会进行线段垂直平分线的性质定理的证明.
2.理解并能灵活运用线段垂直平分线的性质.
3.会作最短路径的问题.
冀教版八上
新课学习
B
A
O
P
M
N
如图,直线MN垂直平分线段AB,点P为MN上一点,连接PA,PB,你认为PA与PB之间具有什么关系?你能证明吗?
问题:
∵线段AB是轴对称图形,中垂线是其对称轴
∴当AB沿对称轴对折后,点A,B重合.
①用对称的知识说明:
B
A
O
P
M
N
新课学习
证明:∵MN ⊥ AB(已知)
∴∠AOP=∠BOP=90(垂直定义)
在△AOP与△ BOP中
∵ AO=BO(已知)
∠AOP=∠BOP(已证)
PO=PO(公共边)
∴ △ AOP≌ △ BOP(SAS)
∴ PA=PB(全等三角形对应边相等)
②用全等的知识进行推理:
B
A
O
P
M
N
新课学习
请用语言描述你证明出的结论:
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段的两端点的距离是相等的.
新课学习
新课学习
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两端点的距离相等.
B
A
O
P
M
N
AB
MN
P
点A、点B
PA、PB
新课学习
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两端点的距离相等.
几何语言:
∵MN垂直平分AB.
∴PA=PB.
用途:
推出相等的线段.
B
A
O
P
M
N
巩固练习
1.如图1所示,直线CD是线段PB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
P
A
B
C
D
2.如图2所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
图1
A
B
C
D
E
图2
B
10cm
典例精析
例题. 已知:如图,点A,B是直线l外任意两点,在直线l上,试确定一点P,使得AP+BP最短.
l
A
B
解:作点A关于直线l的对称点A',连接A'B ,交直线l于点P,则AP+BP最短.
A'
P
思考:
哪个知识点可以用来说明距离最短的问题?
两点之间线段最短.
典例精析
l
A
B
A'
P
由作图可知,l是AA'的中垂线
在l上另取一点M,连接MA,MB,MA'
∴AP=A'P,AM=A'M
∴AP+BP=A'P+BP=A'B
AM+BM=A'M+BM
由“两点之间线段最短”可得A'B<A'M+BM
即AP+BP最短
证明:
M
巩固练习
1.如图,A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边的什么地方,可使所修的渠道最短?
2.连接A'B,交a于点P.
作法:1.做点A关于a的对称点A'.
点P即为抽水站的位置.
A
B
a
A'
P
巩固练习
2.如图,点D在BC上,DE垂直平分AC,垂足为E,DF垂直平分BA,垂足为F,求证:DB=DC.
F
E
D
C
B
A
证明:连接AD
∵DE垂直平分AC
∴DA=DC
同理,DA=DB
∴DB=DC
课堂小测
A.AM>CN B.AM=CN C.AM<CN D.无法确定
1.如图,已知线段AB,BC的中垂线 交于点M,则线段AM,CM的大小关系是( )
B
A
C
M
B
课堂小测
2.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( ).
A.AB=AD B.AC平分∠BCD C.AB=BD D.△BEC≌△DEC
B
A
D
C
E
C
课堂小测
3.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠AOC=120°,则∠ABC= _____.
B
A
D
C
O
60°
课堂小测
4.如图,在△ABC中,AB=AC,D是AB的中点,且DE⊥AB,已知△BCD的周长为12,且AC-BC=2,求AC,BC的长.
A
B
C
D
E
解:∵D是AB的中点,DE⊥AB.
∴DE为AB的中垂线.
∴AE=BE.
∵△BCE的周长为12.
∴BC+CE+BE=12.
∴AC+BC=12.
∵AC-BC=2.
∴AC=7,BC=5.
课堂小结
线段的垂直平分的性质定理
性质
内容
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
实际运用
同学们再见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
