16.3角的平分线-冀教版八年级数学上册课件(共28张ppt)
文档属性
| 名称 | 16.3角的平分线-冀教版八年级数学上册课件(共28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 20:45:20 | ||
图片预览








文档简介
16.3
角的平分线
第十六章
轴对称和中心对称
冀教版八上
学
习
目
标
冀教版八上
1.理解并掌握角平分线的性质定理及其逆定理.
2.能利用角平分线的性质定理及其逆定理证明相关结论并应用.
3.能利用尺规作出一个已知角的角平分线.
旧知链接
1.下图中表示点P到直线l的距离的是
.
线段PC的长
P
l
A
B
C
D
点到直线的距离是指:点到直线的垂线段的长度.
旧知链接
2.本章中,从哪些方面学习线段的中垂线?
①线段中垂线的定义
③线段中垂线的性质定理
④线段中垂线的性质定理的逆定理
⑤线段中垂线的尺规作图
类似地,今天我们将从这些角度学分线的相关知识......
②线段的轴对称性
新课学习
一、角的对称性
如图,OC是∠AOB的平分线,当沿OC所在的直线对折时,∠AOB两旁的部分会重合,因此∠AOB关于OC所在的直线对称.
A
O
B
C
角是轴对称图形
对称轴是角平分线所在的直线
新课学习
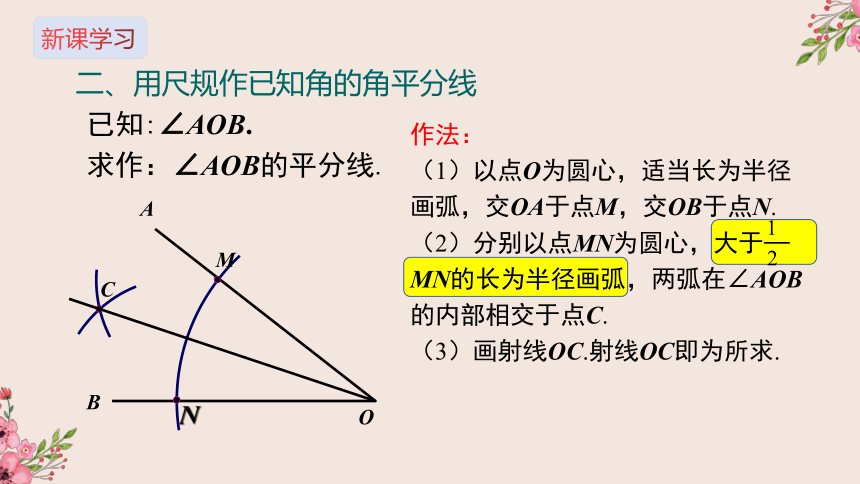
二、用尺规作已知角的角平分线
A
B
M
N
C
O
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点MN为圆心,大于
MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
新课学习
A
B
M
N
C
O
证明:连接CM,CN
由作图过程知,OM=ON,CM=CN,又OC=OC
∴△OMC≌△ONC
∴∠AOC=∠BOC
即OC是∠AOB的角平分线.
试一试:在练习本上分别作锐角,钝角,平角的角平分线.
新课学习
三、角平分线的性质定理
用尺规画∠AOB的平分线OC,,在OC上任取一点P,作出点P到OA,OB的距离,即图中的垂线段PD,PE.PD与PE有何数量关系呢?
P
A
O
B
C
D
E
探究:
你能用什么方法说明你的结论是正确的?
PD=PE
用刻度尺测量PD,PE,得到两条线段的长度相等.
P
A
O
B
C
D
E
新课学习
方法一:
方法二:
利用角的对称性,当沿OC所在的直线对折时,PD与PE重合,因此PD=PE.
P
A
O
B
C
D
E
证明:
∵
PD⊥OA,PE⊥OB,
∴
∠PDO=
∠PEO=90
°.
在△PDO和△PEO中,
∠PDO=
∠PEO,
∠AOC=
∠BOC,
OP=
OP,
∴
△PDO
≌
△PEO(AAS).
∴PD=PE.
新课学习
方法三:
角的平分线上的点到角的两边的距离相等.
请你用语言描述你所得到的结论
用途:
证明两条垂线段相等.
B
A
D
O
P
E
C
新课学习
试一试:
角平分线的性质定理
几何语言:
∵OP
是∠AOB的平分线,
∴PD
=
PE
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
新课学习
注意:一定要表明是两条垂线段.
精准辨析,提升认知
(1)∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
角的平分线上的点到这个角的两边的距离相等
BD
CD
×
B
A
D
C
判断下列的写法是否正确?
理由:
没有垂直,不能确定BD,CD是点D到角两边的距离.
(2)∵
如图,
DC⊥AC,DB⊥AB
(已知).
∴
=
,
(
)
角内任意一条线上的点到这个角的两边的距离相等
BD
CD
×
B
A
D
C
精准辨析,提升认知
理由:无法确定点D在∠BAC的角平分线上.
1.下列各图中,OP是∠MON的角平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角的平分线上的点到角的两边距离相等”的图形是(
).
D
巩固练习
E
N
O
G
F
M
E
N
O
G
F
M
E
N
O
G
F
M
E
N
O
G
F
M
G
A
B
C
D
P
P
P
P
2.如图,在△ABC中,∠C=90°,AC=8,AD=3CD,BD平分∠ABC,则点D到AB的距离等于(
).
C
巩固练习
A
C
D
B
A.4
B.3
C.2
D.1
新课学习
线段的垂直平分线的性质定理有逆定理,角的平分线的性质定理是否也有逆定理呢?
请你说出角平分线的性质定理的逆命题
如果一个点到角两边的距离相等,那么这个点在角的平分线上.
四、角平分线性质定理的逆定理
到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
新课学习
用途:
证明点在角平分线上,即可以判定角平分线.
在17章进行证明
几何语言:
∵
PD⊥OA,PE⊥OB,PD=PE.
∴点P
在∠AOB的平分线上.
新课学习
P
A
O
B
C
D
E
∴OP
是∠AOB的角平分线.
典例精析
例题
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
A
B
C
P
N
M
典例精析
D
E
F
A
B
C
P
N
M
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,PD⊥AB,PE⊥BC,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
典例精析
思考:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
点P在∠A的平分线上.
D
E
F
A
B
C
P
N
M
结论:三角形的三条角平分线交于一点,这点到三角形三边的距离相等.
课堂小测
1.如图,已知四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是______.
D
A
B
C
B
A.24
B.30
C.36
D.42
课堂小测
125°
2.如图,O是△ABC内一点,且点O到三边AB,BC,AC的距离OF=OD=OE,若∠BAC=70°,则∠BOC=______.
F
D
E
A
B
C
O
3.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
课堂小测
课堂小测
4.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上,
FG⊥AE,
FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上,
FH⊥AD,
FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
课堂小结
角的平分线
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
性质定理的逆定理
内容
到角两边距离相等的点在这个角的平分线上
作用
判断一个点是否在角的平分线上
辅助线
添加
过角平分线上一点向两边作垂线段
同学们再见
角的平分线
第十六章
轴对称和中心对称
冀教版八上
学
习
目
标
冀教版八上
1.理解并掌握角平分线的性质定理及其逆定理.
2.能利用角平分线的性质定理及其逆定理证明相关结论并应用.
3.能利用尺规作出一个已知角的角平分线.
旧知链接
1.下图中表示点P到直线l的距离的是
.
线段PC的长
P
l
A
B
C
D
点到直线的距离是指:点到直线的垂线段的长度.
旧知链接
2.本章中,从哪些方面学习线段的中垂线?
①线段中垂线的定义
③线段中垂线的性质定理
④线段中垂线的性质定理的逆定理
⑤线段中垂线的尺规作图
类似地,今天我们将从这些角度学分线的相关知识......
②线段的轴对称性
新课学习
一、角的对称性
如图,OC是∠AOB的平分线,当沿OC所在的直线对折时,∠AOB两旁的部分会重合,因此∠AOB关于OC所在的直线对称.
A
O
B
C
角是轴对称图形
对称轴是角平分线所在的直线
新课学习
二、用尺规作已知角的角平分线
A
B
M
N
C
O
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点MN为圆心,大于
MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
新课学习
A
B
M
N
C
O
证明:连接CM,CN
由作图过程知,OM=ON,CM=CN,又OC=OC
∴△OMC≌△ONC
∴∠AOC=∠BOC
即OC是∠AOB的角平分线.
试一试:在练习本上分别作锐角,钝角,平角的角平分线.
新课学习
三、角平分线的性质定理
用尺规画∠AOB的平分线OC,,在OC上任取一点P,作出点P到OA,OB的距离,即图中的垂线段PD,PE.PD与PE有何数量关系呢?
P
A
O
B
C
D
E
探究:
你能用什么方法说明你的结论是正确的?
PD=PE
用刻度尺测量PD,PE,得到两条线段的长度相等.
P
A
O
B
C
D
E
新课学习
方法一:
方法二:
利用角的对称性,当沿OC所在的直线对折时,PD与PE重合,因此PD=PE.
P
A
O
B
C
D
E
证明:
∵
PD⊥OA,PE⊥OB,
∴
∠PDO=
∠PEO=90
°.
在△PDO和△PEO中,
∠PDO=
∠PEO,
∠AOC=
∠BOC,
OP=
OP,
∴
△PDO
≌
△PEO(AAS).
∴PD=PE.
新课学习
方法三:
角的平分线上的点到角的两边的距离相等.
请你用语言描述你所得到的结论
用途:
证明两条垂线段相等.
B
A
D
O
P
E
C
新课学习
试一试:
角平分线的性质定理
几何语言:
∵OP
是∠AOB的平分线,
∴PD
=
PE
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
新课学习
注意:一定要表明是两条垂线段.
精准辨析,提升认知
(1)∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
角的平分线上的点到这个角的两边的距离相等
BD
CD
×
B
A
D
C
判断下列的写法是否正确?
理由:
没有垂直,不能确定BD,CD是点D到角两边的距离.
(2)∵
如图,
DC⊥AC,DB⊥AB
(已知).
∴
=
,
(
)
角内任意一条线上的点到这个角的两边的距离相等
BD
CD
×
B
A
D
C
精准辨析,提升认知
理由:无法确定点D在∠BAC的角平分线上.
1.下列各图中,OP是∠MON的角平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角的平分线上的点到角的两边距离相等”的图形是(
).
D
巩固练习
E
N
O
G
F
M
E
N
O
G
F
M
E
N
O
G
F
M
E
N
O
G
F
M
G
A
B
C
D
P
P
P
P
2.如图,在△ABC中,∠C=90°,AC=8,AD=3CD,BD平分∠ABC,则点D到AB的距离等于(
).
C
巩固练习
A
C
D
B
A.4
B.3
C.2
D.1
新课学习
线段的垂直平分线的性质定理有逆定理,角的平分线的性质定理是否也有逆定理呢?
请你说出角平分线的性质定理的逆命题
如果一个点到角两边的距离相等,那么这个点在角的平分线上.
四、角平分线性质定理的逆定理
到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
新课学习
用途:
证明点在角平分线上,即可以判定角平分线.
在17章进行证明
几何语言:
∵
PD⊥OA,PE⊥OB,PD=PE.
∴点P
在∠AOB的平分线上.
新课学习
P
A
O
B
C
D
E
∴OP
是∠AOB的角平分线.
典例精析
例题
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
A
B
C
P
N
M
典例精析
D
E
F
A
B
C
P
N
M
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,PD⊥AB,PE⊥BC,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
典例精析
思考:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
点P在∠A的平分线上.
D
E
F
A
B
C
P
N
M
结论:三角形的三条角平分线交于一点,这点到三角形三边的距离相等.
课堂小测
1.如图,已知四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是______.
D
A
B
C
B
A.24
B.30
C.36
D.42
课堂小测
125°
2.如图,O是△ABC内一点,且点O到三边AB,BC,AC的距离OF=OD=OE,若∠BAC=70°,则∠BOC=______.
F
D
E
A
B
C
O
3.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
课堂小测
课堂小测
4.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上,
FG⊥AE,
FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上,
FH⊥AD,
FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
课堂小结
角的平分线
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
性质定理的逆定理
内容
到角两边距离相等的点在这个角的平分线上
作用
判断一个点是否在角的平分线上
辅助线
添加
过角平分线上一点向两边作垂线段
同学们再见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
