2020年北师大版九年级数学下册1.5《三角函数的应用》课件(共16张ppt)
文档属性
| 名称 | 2020年北师大版九年级数学下册1.5《三角函数的应用》课件(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 11:10:08 | ||
图片预览






文档简介
1.5 三角函数的应用
北师大版九年级数学下册
直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=900.
直角三角形的边角关系
直角三角形三边的关系: 勾股定理 a2+b2=c2.
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sinA=cosB.
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:锐角三角函数
同角之间的三角函数关系:
sin2A+cos2A=1.
知识回顾
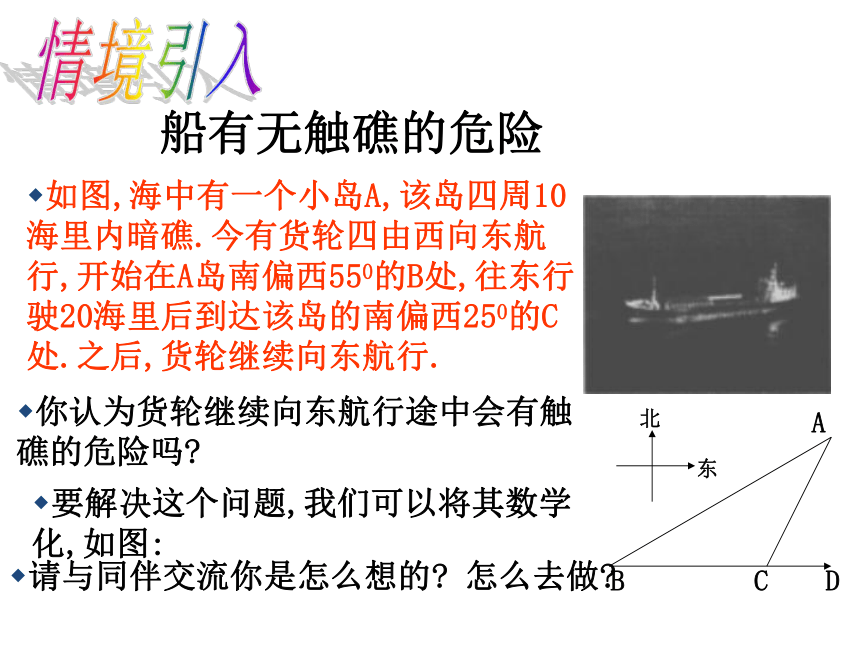
船有无触礁的危险
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.
要解决这个问题,我们可以将其数学化,如图:
请与同伴交流你是怎么想的? 怎么去做?
你认为货轮继续向东航行途中会有触礁的危险吗?
A
B
C
D
北
东
情境引入
解:要知道货轮继续向东航行途中有无触礁的危险,只要过点A作AD⊥BC的延长线于点D,如果AD>10海里,则无触礁的危险.根据题意可知,∠BAD=550,∠CAD=250,BC= 20海里.设AD=x,则
答:货轮继续向东航行途中没有触礁的危险.
D
┌
A
B
C
D
北
东
550
250
自主预习
看我露一手
古塔究竟有多高
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
要解决这问题,我们仍需将其数学化.
请与同伴交流你是怎么想的? 准备怎么去做?
现在你能完成这个任务吗?
行家看“门道”
这个图形与前面的图形相同,因此解答如下:
D
A
B
C
┌
50m
300
600
答:该塔约有43m高.
解:如图,根据题意可知,∠A=300,∠DBC=600,AB=50m.设CD=x,则∠ADC=600, ∠BDC=300,
老师期望:这道题你能有更简单的解法.
新知探究
试试自己的分析能力
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).
现在你能完成这个任务吗?
请与同伴交流你是怎么想的? 准备怎么去做?
A
B
C
D
┌
我是最棒的!
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(1)AB-BD的长,(2)AD的长.
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
成功在于坚持
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(2) AD的长.
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
你会计算吗?
如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).
怎么做?
E
B
C
D
2m
400
5m
我高兴,我会做
解:如图,根据题意可知,∠CDB=400,EC=2m,DB=5m.求DE的长.
∴∠BDE≈51.12°.
E
B
C
D
2m
400
5m
答:钢缆ED的长度约为7.97m.
都来当个小专家!
2 如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=1350.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).
咋办
先构造直角三角形!
A
B
C
D
你会构建两个直角三角形求解吗?
解:如图,(1)求坡角∠ABC的大小;
有两个直角三角形
先做辅助线!
A
B
C
D
6m
8m
30m
1350
过点D作DE⊥BC于点E,过点A作AF⊥BC于点F.
E
┐
F
┌
∴∠ABC≈13°.
答:坡角∠ABC约为13°.
这种体积你会算吗?
解:如图,(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).
答:修建这个大坝共需土石方约10182.34m3.
100m
A
B
C
D
6m
8m
30m
1350
E
┐
F
┌
1 如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.
2.有一建筑物,在地面上A点测得其顶点C的仰角为300,向建筑物前进50m至B处,又测得C的仰角为450,求该建筑物的高度(结果精确到0.1m).
3. 如图,燕尾槽的横断面是一个等腰梯形,其中燕尾角∠B=550,外口宽AD=180mm,燕尾槽的尝试是70mm,求它的里口宽BC(结果精确到1mm).
A
B
C
┌
A
B
C
D
随堂练习
我们发现以上几个问题的解决方法,都是首先构建直角三角形,在两个直角三角形中运用边角关系分步解决。此类题型需要大家冷静分析,认真解答。
通过本节课的学习你又增长了哪些知识?
知识梳理
知识梳理
从已知的边和角
未知的边和角
表示
求出答案
北师大版九年级数学下册
直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=900.
直角三角形的边角关系
直角三角形三边的关系: 勾股定理 a2+b2=c2.
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sinA=cosB.
特殊角300,450,600角的三角函数值.
直角三角形边与角之间的关系:锐角三角函数
同角之间的三角函数关系:
sin2A+cos2A=1.
知识回顾
船有无触礁的危险
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.
要解决这个问题,我们可以将其数学化,如图:
请与同伴交流你是怎么想的? 怎么去做?
你认为货轮继续向东航行途中会有触礁的危险吗?
A
B
C
D
北
东
情境引入
解:要知道货轮继续向东航行途中有无触礁的危险,只要过点A作AD⊥BC的延长线于点D,如果AD>10海里,则无触礁的危险.根据题意可知,∠BAD=550,∠CAD=250,BC= 20海里.设AD=x,则
答:货轮继续向东航行途中没有触礁的危险.
D
┌
A
B
C
D
北
东
550
250
自主预习
看我露一手
古塔究竟有多高
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
要解决这问题,我们仍需将其数学化.
请与同伴交流你是怎么想的? 准备怎么去做?
现在你能完成这个任务吗?
行家看“门道”
这个图形与前面的图形相同,因此解答如下:
D
A
B
C
┌
50m
300
600
答:该塔约有43m高.
解:如图,根据题意可知,∠A=300,∠DBC=600,AB=50m.设CD=x,则∠ADC=600, ∠BDC=300,
老师期望:这道题你能有更简单的解法.
新知探究
试试自己的分析能力
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).
现在你能完成这个任务吗?
请与同伴交流你是怎么想的? 准备怎么去做?
A
B
C
D
┌
我是最棒的!
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(1)AB-BD的长,(2)AD的长.
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
成功在于坚持
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(2) AD的长.
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
你会计算吗?
如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).
怎么做?
E
B
C
D
2m
400
5m
我高兴,我会做
解:如图,根据题意可知,∠CDB=400,EC=2m,DB=5m.求DE的长.
∴∠BDE≈51.12°.
E
B
C
D
2m
400
5m
答:钢缆ED的长度约为7.97m.
都来当个小专家!
2 如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=1350.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).
咋办
先构造直角三角形!
A
B
C
D
你会构建两个直角三角形求解吗?
解:如图,(1)求坡角∠ABC的大小;
有两个直角三角形
先做辅助线!
A
B
C
D
6m
8m
30m
1350
过点D作DE⊥BC于点E,过点A作AF⊥BC于点F.
E
┐
F
┌
∴∠ABC≈13°.
答:坡角∠ABC约为13°.
这种体积你会算吗?
解:如图,(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).
答:修建这个大坝共需土石方约10182.34m3.
100m
A
B
C
D
6m
8m
30m
1350
E
┐
F
┌
1 如图,有一斜坡AB长40m,坡顶离地面的高度为20m,求此斜坡的倾斜角.
2.有一建筑物,在地面上A点测得其顶点C的仰角为300,向建筑物前进50m至B处,又测得C的仰角为450,求该建筑物的高度(结果精确到0.1m).
3. 如图,燕尾槽的横断面是一个等腰梯形,其中燕尾角∠B=550,外口宽AD=180mm,燕尾槽的尝试是70mm,求它的里口宽BC(结果精确到1mm).
A
B
C
┌
A
B
C
D
随堂练习
我们发现以上几个问题的解决方法,都是首先构建直角三角形,在两个直角三角形中运用边角关系分步解决。此类题型需要大家冷静分析,认真解答。
通过本节课的学习你又增长了哪些知识?
知识梳理
知识梳理
从已知的边和角
未知的边和角
表示
求出答案
