北师大版九年级上册4.8.1 图形的位似课件(23张PPT)
文档属性
| 名称 | 北师大版九年级上册4.8.1 图形的位似课件(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 19:49:29 | ||
图片预览




文档简介
第四章 图形的相似
第8节 图形的位似(一)
九年级(1)班的同学们准备召开一次班会,他们想把下面的图样放大,使放大前后对应线段的比为1︰2,然后制成彩纸活跃气氛,请你帮助他们找到放大图样的方法。
问题导入
问题的关键在于要改变图形的大小,但不能改变图形的形状。
以上五幅图片是形状相同的图形,取图中相对应的两点A、B,它们的连线经过镜头中心P吗?换其他的对应点试一试,还有类似规律吗?
每一组对应点的连线都经过镜头中心点P
观察思考
观察思考
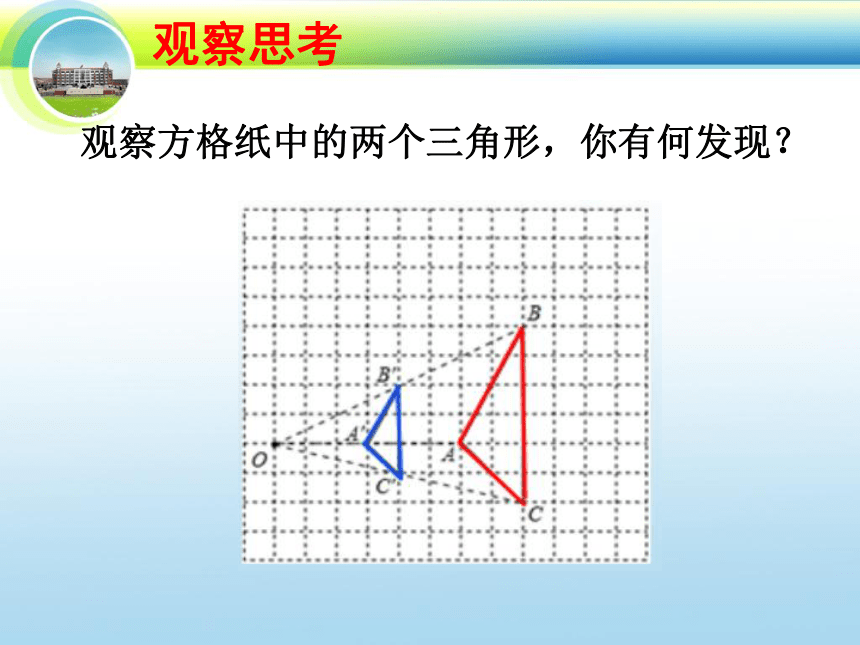
观察方格纸中的两个三角形,你有何发现?
2.
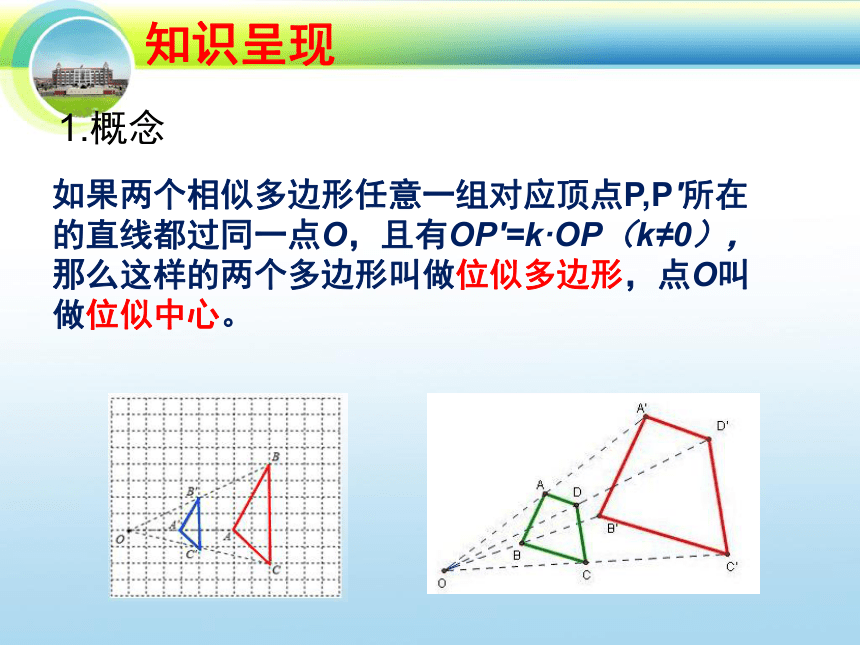
如果两个相似多边形任意一组对应顶点P,P′所在的直线都过同一点O,且有OP′=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心。
知识呈现
1.概念
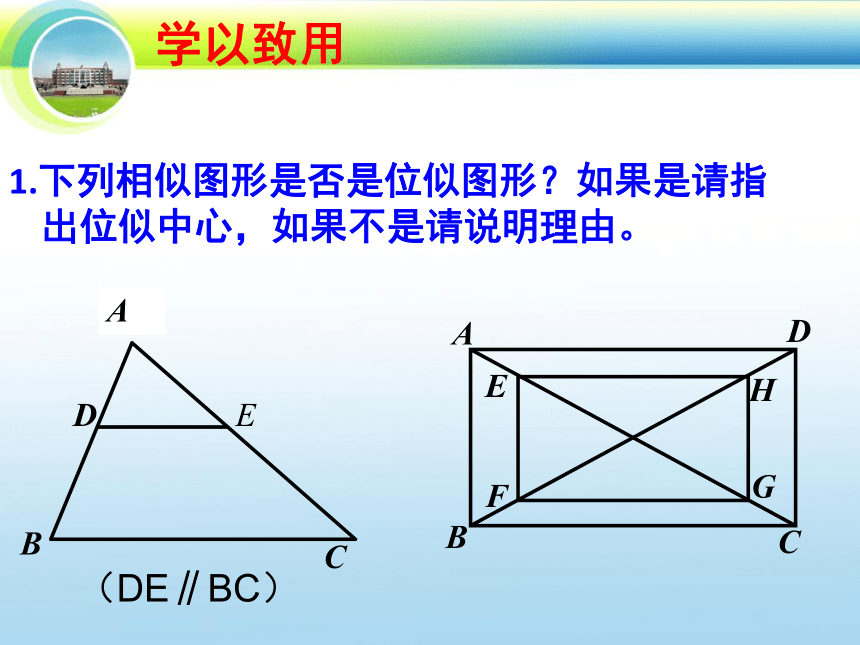
1.下列相似图形是否是位似图形?如果是请指出位似中心,如果不是请说明理由。
B
A
C
E
D
F
E
D
C
B
A
H
G
学以致用
(DE∥BC)
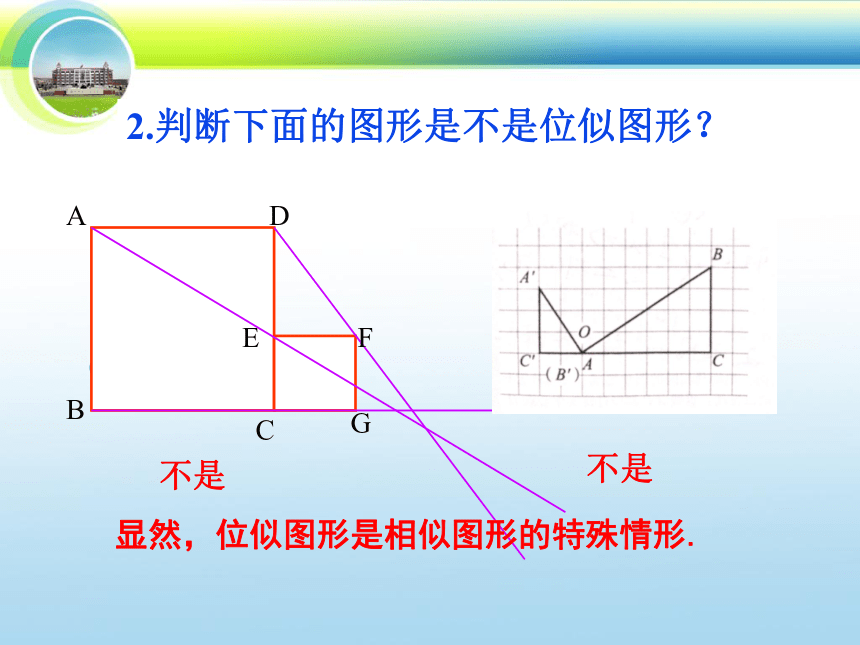
2.判断下面的图形是不是位似图形?
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.
不是
1. 两图形相似
2. 每组对应点所在直线都经过同一点
3. OP'=kOP(k≠0,P,P’为对应点)
判断两图形是否是位似图形的“三要求”
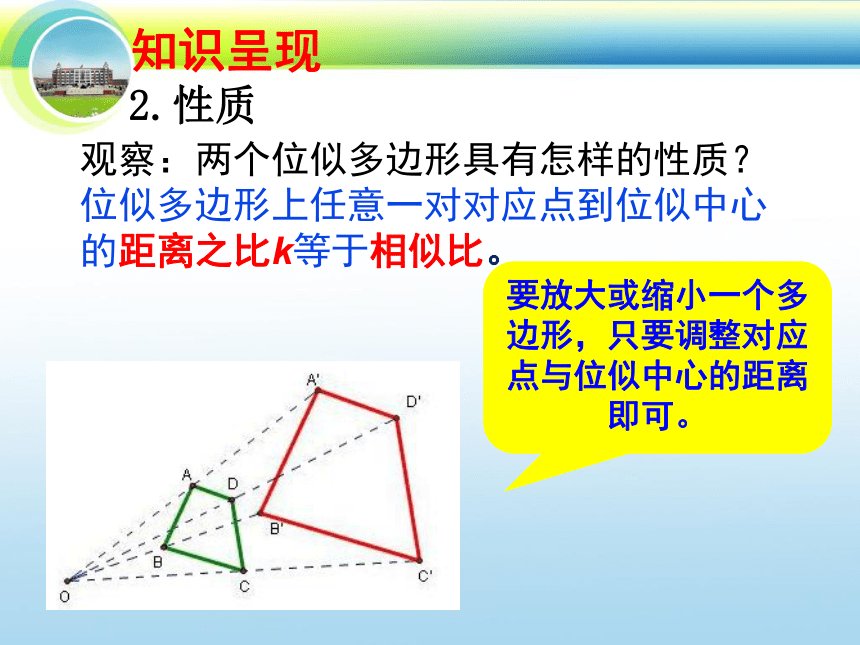
位似多边形上任意一对对应点到位似中心的距离之比k等于相似比。
知识呈现
2.性质
观察:两个位似多边形具有怎样的性质?
要放大或缩小一个多边形,只要调整对应点与位似中心的距离即可。
1.如图:五边形ABCDE与五边形A'B'C'D'E'是位似图形。O为位似中心,若OD:O'D'=1:2,则A'B':AB的值为______.
O
A
A'
C'
C
B'
B
2.如图ΔABC与ΔA'B'C'为位似图形,点O是它们的位似中心,位似比是1:2,已知ΔABC的面积是3,那么ΔA'B'C'的面积是___________。
巩固练习
请观察:以上每组图中的两个多边形是位似多边形,位似中心在哪里?
你能把它们分类吗?
图(2)(3)(5)中对应点在位似中心的同一侧,图(1)(4)(6)中对应点在位似中心的两侧。两种方法都能起到把图形放大或缩小的效果。
已知△ABC,以O为位似中心画一个△DEF,使它与△ABC位似,并且相似比为2。
动手实践
O
A
B
C
D
E
F
D
E
△DEF即为所求作的三角形
2.已知O在△ABC内,以O为位似中心画一个三角形,使它与△ABC位似,
且相似比为 .
自己动手试一试,并向同学们展示一下你的作法。
A
B
C
动手实践
·O
下面请你回顾一下本节课开篇时的问题,请你与同学探讨一下如何帮助九年级(1)班的同学完成图样的放大。
问题回放
用以下方法可以近似地 把一个不规则图形放大:
拓展延伸
1.将两根等长的橡皮 系在一起,连接处形成一个结点。
2.选一个图形,再选一 个定点,将橡皮筋的一 端固定在定点处,把铅笔固定在另一端。
3.拉动铅笔,使结点沿图形的边缘移动一周,这样铅笔就画出一个新的图形。试试看,它们相似吗?
拓展延伸
课堂小结
本堂课你学到了什么?请你与同学们交流一下?
1.概念:什么是位似多边形?
2.性质:位似多边形有哪些性质?
3.作用:如何利用位似将图形放大或缩小?
(2)相似多边形一定是位似多边形。
(1)位似多边形一定是相似多边形。
(3)两个位似多边形每一对对应点到位似中心的距离之比为2︰3,则两个多边形的面积之比为4︰9。
1、判断正误:
(4)两个位似多边形的对应边互相平行或在同一直线上。
达标检测
2.如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9
3.如图所示,这是圆桌正上方的灯泡(看作一点),发出的光线照射到桌面后,在地面上形成的阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为________米2.
5.如图,方格纸中(每个小方格的边长都是1个单位)有一△ABC.
(1)将△ABC以点B为位似中心放大到2倍,得△A1B1C1.
(2)以任意一点为位似中心,将△ABC缩小到原来△ABC缩小到原来的一半.
作业布置
1.学案剩余题目
2.课本课后习题
人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机。——席慕蓉
第8节 图形的位似(一)
九年级(1)班的同学们准备召开一次班会,他们想把下面的图样放大,使放大前后对应线段的比为1︰2,然后制成彩纸活跃气氛,请你帮助他们找到放大图样的方法。
问题导入
问题的关键在于要改变图形的大小,但不能改变图形的形状。
以上五幅图片是形状相同的图形,取图中相对应的两点A、B,它们的连线经过镜头中心P吗?换其他的对应点试一试,还有类似规律吗?
每一组对应点的连线都经过镜头中心点P
观察思考
观察思考
观察方格纸中的两个三角形,你有何发现?
2.
如果两个相似多边形任意一组对应顶点P,P′所在的直线都过同一点O,且有OP′=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心。
知识呈现
1.概念
1.下列相似图形是否是位似图形?如果是请指出位似中心,如果不是请说明理由。
B
A
C
E
D
F
E
D
C
B
A
H
G
学以致用
(DE∥BC)
2.判断下面的图形是不是位似图形?
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.
不是
1. 两图形相似
2. 每组对应点所在直线都经过同一点
3. OP'=kOP(k≠0,P,P’为对应点)
判断两图形是否是位似图形的“三要求”
位似多边形上任意一对对应点到位似中心的距离之比k等于相似比。
知识呈现
2.性质
观察:两个位似多边形具有怎样的性质?
要放大或缩小一个多边形,只要调整对应点与位似中心的距离即可。
1.如图:五边形ABCDE与五边形A'B'C'D'E'是位似图形。O为位似中心,若OD:O'D'=1:2,则A'B':AB的值为______.
O
A
A'
C'
C
B'
B
2.如图ΔABC与ΔA'B'C'为位似图形,点O是它们的位似中心,位似比是1:2,已知ΔABC的面积是3,那么ΔA'B'C'的面积是___________。
巩固练习
请观察:以上每组图中的两个多边形是位似多边形,位似中心在哪里?
你能把它们分类吗?
图(2)(3)(5)中对应点在位似中心的同一侧,图(1)(4)(6)中对应点在位似中心的两侧。两种方法都能起到把图形放大或缩小的效果。
已知△ABC,以O为位似中心画一个△DEF,使它与△ABC位似,并且相似比为2。
动手实践
O
A
B
C
D
E
F
D
E
△DEF即为所求作的三角形
2.已知O在△ABC内,以O为位似中心画一个三角形,使它与△ABC位似,
且相似比为 .
自己动手试一试,并向同学们展示一下你的作法。
A
B
C
动手实践
·O
下面请你回顾一下本节课开篇时的问题,请你与同学探讨一下如何帮助九年级(1)班的同学完成图样的放大。
问题回放
用以下方法可以近似地 把一个不规则图形放大:
拓展延伸
1.将两根等长的橡皮 系在一起,连接处形成一个结点。
2.选一个图形,再选一 个定点,将橡皮筋的一 端固定在定点处,把铅笔固定在另一端。
3.拉动铅笔,使结点沿图形的边缘移动一周,这样铅笔就画出一个新的图形。试试看,它们相似吗?
拓展延伸
课堂小结
本堂课你学到了什么?请你与同学们交流一下?
1.概念:什么是位似多边形?
2.性质:位似多边形有哪些性质?
3.作用:如何利用位似将图形放大或缩小?
(2)相似多边形一定是位似多边形。
(1)位似多边形一定是相似多边形。
(3)两个位似多边形每一对对应点到位似中心的距离之比为2︰3,则两个多边形的面积之比为4︰9。
1、判断正误:
(4)两个位似多边形的对应边互相平行或在同一直线上。
达标检测
2.如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9
3.如图所示,这是圆桌正上方的灯泡(看作一点),发出的光线照射到桌面后,在地面上形成的阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为________米2.
5.如图,方格纸中(每个小方格的边长都是1个单位)有一△ABC.
(1)将△ABC以点B为位似中心放大到2倍,得△A1B1C1.
(2)以任意一点为位似中心,将△ABC缩小到原来△ABC缩小到原来的一半.
作业布置
1.学案剩余题目
2.课本课后习题
人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机。——席慕蓉
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
