北师大版九年级数学上册 6.2《反比例函数的图象与性质(1)》 课件(18张PPT)
文档属性
| 名称 | 北师大版九年级数学上册 6.2《反比例函数的图象与性质(1)》 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 524.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 19:48:31 | ||
图片预览




文档简介
6.2 反比例函数的图象与性质
第一课时
一、知识回顾
一般地,如果两个变量 之间的对应关系可以表示成 的形式,那么称 是 的反比例函数。
反比例函数的自变量不能为零。
反比例函数的三种形式:
(1)一般形式 :
(分式形式)
(2) 乘积形式:
(3) 指数形式:
什么是反比例函数?
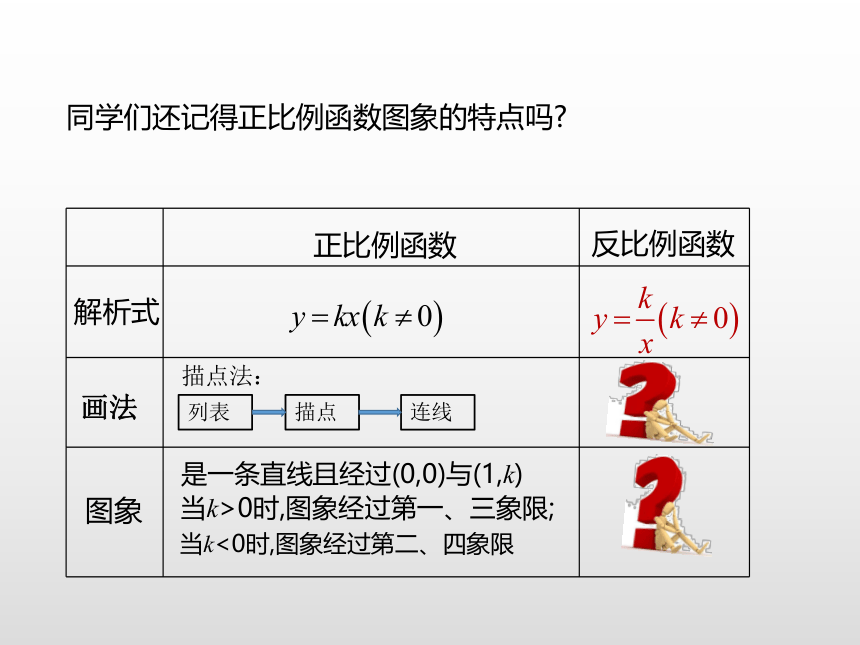
同学们还记得正比例函数图象的特点吗?
?
当k>0时,图象经过第一、三象限;
是一条直线且经过(0,0)与(1,k)
正比例函数
解析式
图象
当k<0时,图象经过第二、四象限
反比例函数
画法
描点法:
列表
描点
连线
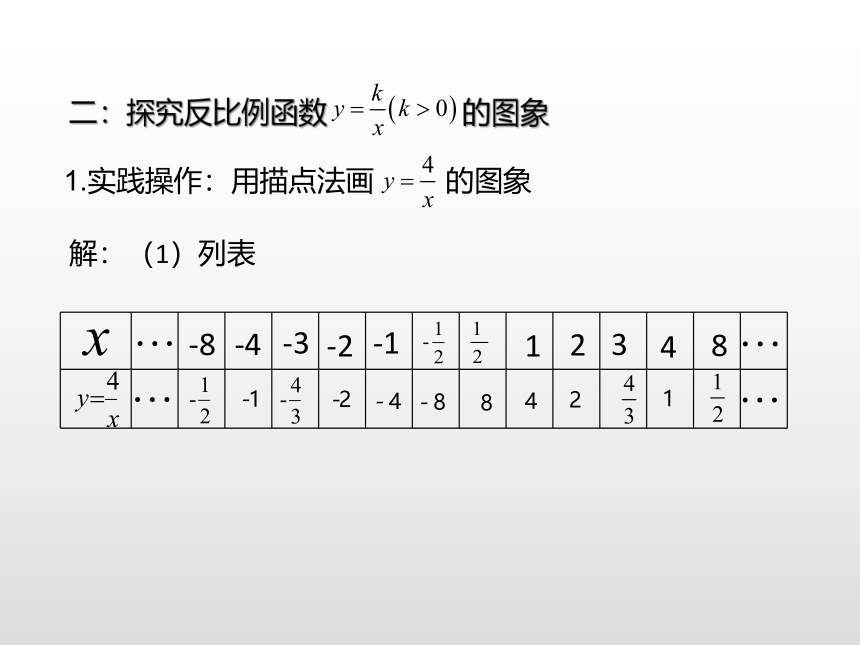
二:探究反比例函数 的图象
1.实践操作:用描点法画 的图象
解:(1)列表
-1
-2
- 4
- 8
8
4
2
1
-8
-4
-3
-2
-1
1
2
3
4
8
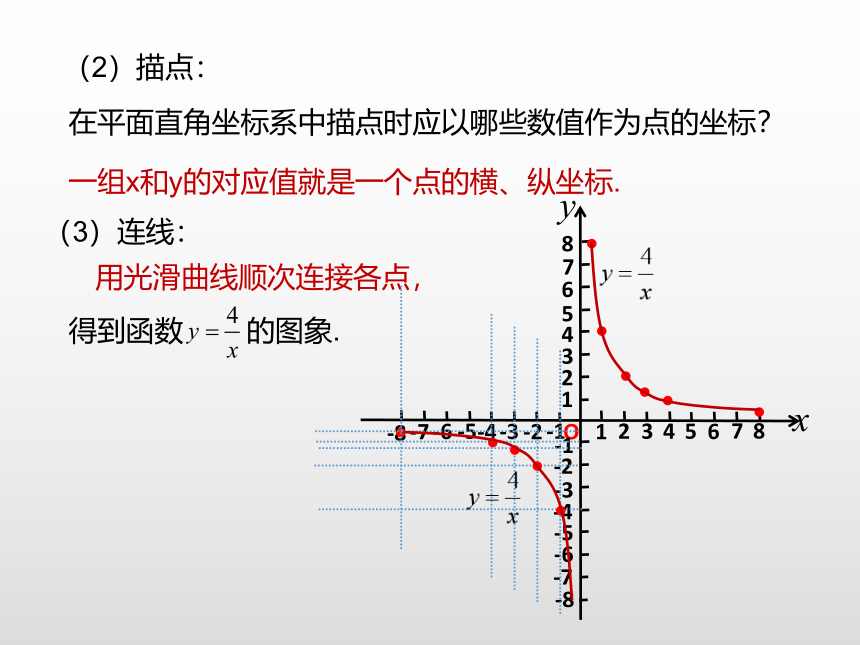
(2)描点:
在平面直角坐标系中描点时应以哪些数值作为点的坐标?
一组x和y的对应值就是一个点的横、纵坐标.
(3)连线:
用光滑曲线顺次连接各点,
O
1
2
3
4
5
6
7
8
-1
-2
-3
-4
-5
-6
-7
1
2
3
4
5
6
7
8
-1
-2
-3
-4
-5
-6
-7
-8
-8
?
?
?
?
?
?
?
?
?
?
?
得到函数 的图象.
思考:
(1)反比例函数 的自变量的取值范围是什么?
(2)画反比例函数 的图象的步骤是什么?
x ≠ 0
列表——描点——连线
(3)列表时应注意什么问题?
①x不能取0; ②列表取值时注意对称性.
(1)图象是两支曲线,分布在第一、三象限.
(2)当x<0时,图象在第三象限,当x>0,图象在第一象限.
(3)它是轴对称图形,对称轴是直线:y=x和y=-x;它是中心对称图形,对称中心是坐标原点.
2.观察探究:观察 这个函数的图象,它有什么特点?
4.其他的反比例函数 的图象是否有同样的特点呢?
(1)列表时,选取的自变量的值,即要易于计算,又要易于描点,尽量多取点,这样使图象更精确;
(2)描点时,严格按照列表中对应值描点,不能描错.
(3)连线时,按横坐标从小到大的顺序用光滑的曲线依次连接各点,不能用折线连接.
(4)根据反比例函数自变量的取值范围可知, 图象是延伸的,且不与坐标轴相交,所以图象中不能有明确的端点,以及与坐标轴的交点.
3.议一议:同学们认为画反比例函数图象时应注意哪些问题?
解:(1)列表
x
…
- 8
- 4
-3
-2
-1
1
2
3
4
8
…
…
…
1
2
4
8
- 8
- 4
- 2
-1
三:探究反比例函数 的图象
1.实践操作:用描点法画 的图象
(2)在平面直角坐标系中描点:
(3)连线:
用光滑曲线顺次连接各点,
得到函数 的图象.
(1)图象是两支曲线,分布在二、四象限.
(2)当x<0时,图象在第二象限,当x>0,图象在第四象限.
(3)它是轴对称图形,对称轴是直线:y=x和y=-x;它是中心对称图形,对称中心是坐标原点.
2.观察探究:观察 这个函数的图象,它有什么特点?
3.其他的反比例函数 的图象是否有同样的特点?
相同点:
图象都是由两支曲线组成的,它们都不与坐标轴相交.
两个函数图象都是轴对称图形,它们都有两条对称轴.
都是中心对称图形,对称中心都是坐标原点.
不同点:
当k=4时,图象的两支分别位于第一、三象限;
k=﹣4时, 图象的两支分别位于第二、四象限.
4. 观察比较:函数 和 的图象有什么相同点和不同点?
反比例函数 的图形特征:
当k>0时, 两支曲线分别位于第一、三象限;k<0时, 两支曲线分别位于第二、四象限.
反比例函数 的图象是既轴对称图形是中心对称图形,有两条对称轴,对称轴是直线y=x和y=-x;对称中心是坐标原点.
归纳总结:反比例函数 的图象
形状:
1、
反比例函数 的图象是由两支曲线组成的.
2、
位置:
3、
对称性:
例题讲解
A.
B.
C.
D.
例1:下列图象中是反比例函数 图象的是( )
D
例2:若ab<0,则正比例函数y=ax和反比例函数 在同一坐标系中的大致图象可能是下图中的 ( )
点拨:
k>0时,正比例函数y=kx和反比例函数 的图象过第一、三象限,但正比例函数过原点,反比例函数不与坐标轴相交;
k<0时,正比例函数y=kx和反比例函数 的图象过第二、四象限,同样正比例函数过原点,反比例函数不与坐标轴相交.
例题讲解
解析:∵ab<0,∴a,b为异号,分两种情况:
(1)当a>0,b<0时,正比例函数y=ax的图象过第一、三象限,经过坐标原点;反比例函数图象在第二、四象限内,无此选项;
(2)当a<0,b>0时,正比例函数的图象过第二、四象限,反比例函数图象在第一、三象限内,选项C符合.
C
解:(1)由题意,点A(-2,1)在反比例函数图象上,
∴ ,解得m=-2. ∴反比例函数表达式为 .
又∵点B(1,n)也在反比例函数图象上,
∴ . ∵点A,B在一次函数图象上,
∴ . 解得 .
∴一次函数表达式为 .
例3:如图,在平面直角坐标系xOy中,一次函数
(a,b为常数,且a≠0)与反比例函数 (m为常数,且m≠0)的图象交于点A(-2,1),B(1,n).
(1)求反比例函数和一次函数的表达式;
反比例函数 (k≠0)的图象是由两支曲线(双曲线)组成的,当k>0时,两支曲线分别位于第一、三象限内;当 k<0时,两支曲线分别位于第二、四象限内.
反比例函数 (k≠0)的图象是轴对称图形,它有两条对称轴,对称轴是直线y=x和y=-x;
它是中心对称图形,对称中心是坐标原点.
小结:
教材第153页随堂练习和教材第154页习题6.2的第1题.
布置作业:
第一课时
一、知识回顾
一般地,如果两个变量 之间的对应关系可以表示成 的形式,那么称 是 的反比例函数。
反比例函数的自变量不能为零。
反比例函数的三种形式:
(1)一般形式 :
(分式形式)
(2) 乘积形式:
(3) 指数形式:
什么是反比例函数?
同学们还记得正比例函数图象的特点吗?
?
当k>0时,图象经过第一、三象限;
是一条直线且经过(0,0)与(1,k)
正比例函数
解析式
图象
当k<0时,图象经过第二、四象限
反比例函数
画法
描点法:
列表
描点
连线
二:探究反比例函数 的图象
1.实践操作:用描点法画 的图象
解:(1)列表
-1
-2
- 4
- 8
8
4
2
1
-8
-4
-3
-2
-1
1
2
3
4
8
(2)描点:
在平面直角坐标系中描点时应以哪些数值作为点的坐标?
一组x和y的对应值就是一个点的横、纵坐标.
(3)连线:
用光滑曲线顺次连接各点,
O
1
2
3
4
5
6
7
8
-1
-2
-3
-4
-5
-6
-7
1
2
3
4
5
6
7
8
-1
-2
-3
-4
-5
-6
-7
-8
-8
?
?
?
?
?
?
?
?
?
?
?
得到函数 的图象.
思考:
(1)反比例函数 的自变量的取值范围是什么?
(2)画反比例函数 的图象的步骤是什么?
x ≠ 0
列表——描点——连线
(3)列表时应注意什么问题?
①x不能取0; ②列表取值时注意对称性.
(1)图象是两支曲线,分布在第一、三象限.
(2)当x<0时,图象在第三象限,当x>0,图象在第一象限.
(3)它是轴对称图形,对称轴是直线:y=x和y=-x;它是中心对称图形,对称中心是坐标原点.
2.观察探究:观察 这个函数的图象,它有什么特点?
4.其他的反比例函数 的图象是否有同样的特点呢?
(1)列表时,选取的自变量的值,即要易于计算,又要易于描点,尽量多取点,这样使图象更精确;
(2)描点时,严格按照列表中对应值描点,不能描错.
(3)连线时,按横坐标从小到大的顺序用光滑的曲线依次连接各点,不能用折线连接.
(4)根据反比例函数自变量的取值范围可知, 图象是延伸的,且不与坐标轴相交,所以图象中不能有明确的端点,以及与坐标轴的交点.
3.议一议:同学们认为画反比例函数图象时应注意哪些问题?
解:(1)列表
x
…
- 8
- 4
-3
-2
-1
1
2
3
4
8
…
…
…
1
2
4
8
- 8
- 4
- 2
-1
三:探究反比例函数 的图象
1.实践操作:用描点法画 的图象
(2)在平面直角坐标系中描点:
(3)连线:
用光滑曲线顺次连接各点,
得到函数 的图象.
(1)图象是两支曲线,分布在二、四象限.
(2)当x<0时,图象在第二象限,当x>0,图象在第四象限.
(3)它是轴对称图形,对称轴是直线:y=x和y=-x;它是中心对称图形,对称中心是坐标原点.
2.观察探究:观察 这个函数的图象,它有什么特点?
3.其他的反比例函数 的图象是否有同样的特点?
相同点:
图象都是由两支曲线组成的,它们都不与坐标轴相交.
两个函数图象都是轴对称图形,它们都有两条对称轴.
都是中心对称图形,对称中心都是坐标原点.
不同点:
当k=4时,图象的两支分别位于第一、三象限;
k=﹣4时, 图象的两支分别位于第二、四象限.
4. 观察比较:函数 和 的图象有什么相同点和不同点?
反比例函数 的图形特征:
当k>0时, 两支曲线分别位于第一、三象限;k<0时, 两支曲线分别位于第二、四象限.
反比例函数 的图象是既轴对称图形是中心对称图形,有两条对称轴,对称轴是直线y=x和y=-x;对称中心是坐标原点.
归纳总结:反比例函数 的图象
形状:
1、
反比例函数 的图象是由两支曲线组成的.
2、
位置:
3、
对称性:
例题讲解
A.
B.
C.
D.
例1:下列图象中是反比例函数 图象的是( )
D
例2:若ab<0,则正比例函数y=ax和反比例函数 在同一坐标系中的大致图象可能是下图中的 ( )
点拨:
k>0时,正比例函数y=kx和反比例函数 的图象过第一、三象限,但正比例函数过原点,反比例函数不与坐标轴相交;
k<0时,正比例函数y=kx和反比例函数 的图象过第二、四象限,同样正比例函数过原点,反比例函数不与坐标轴相交.
例题讲解
解析:∵ab<0,∴a,b为异号,分两种情况:
(1)当a>0,b<0时,正比例函数y=ax的图象过第一、三象限,经过坐标原点;反比例函数图象在第二、四象限内,无此选项;
(2)当a<0,b>0时,正比例函数的图象过第二、四象限,反比例函数图象在第一、三象限内,选项C符合.
C
解:(1)由题意,点A(-2,1)在反比例函数图象上,
∴ ,解得m=-2. ∴反比例函数表达式为 .
又∵点B(1,n)也在反比例函数图象上,
∴ . ∵点A,B在一次函数图象上,
∴ . 解得 .
∴一次函数表达式为 .
例3:如图,在平面直角坐标系xOy中,一次函数
(a,b为常数,且a≠0)与反比例函数 (m为常数,且m≠0)的图象交于点A(-2,1),B(1,n).
(1)求反比例函数和一次函数的表达式;
反比例函数 (k≠0)的图象是由两支曲线(双曲线)组成的,当k>0时,两支曲线分别位于第一、三象限内;当 k<0时,两支曲线分别位于第二、四象限内.
反比例函数 (k≠0)的图象是轴对称图形,它有两条对称轴,对称轴是直线y=x和y=-x;
它是中心对称图形,对称中心是坐标原点.
小结:
教材第153页随堂练习和教材第154页习题6.2的第1题.
布置作业:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
