北师大版九年级数学上册:6.2《反比例函数的图象与性质(2)》
文档属性
| 名称 | 北师大版九年级数学上册:6.2《反比例函数的图象与性质(2)》 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 11:13:51 | ||
图片预览






文档简介
6.2 反比例函数的图象与性质
第二课时
同学们还记得反比例函数图象的画法和特点吗?
一、回顾与思考
画法:
(1):列表
(2):描点
(3):连线
特点:
(1)形状:
反比例函数 的图象是由两支曲线组成的.
(2)位置:
当k>0时, 两支曲线分别位于第一、三象限;k<0时, 两支曲线分别位于第二、四象限.
(3)对称性:
反比例函数 的图象是既轴对称图形是中心对称图形,有两条对称轴,对称轴是直线y=x和y=-x;对称中心是坐标原点.
(1)列表时,选取的自变量的值,即要易于计算,又要易于描点,尽量多取点,这样使图象更精确;
(2)描点时,严格按照列表中对应值描点,不能描错.
(3)连线时,按横坐标从小到大的顺序用光滑的曲线依次连接各点,不能用折线连接.
(4)根据反比例函数自变量的取值范围可知, 图象是延伸的,且不与坐标轴相交,所以图象中不能有明确的端点,以及与坐标轴的交点.
画反比例函数图象时应注意的问题:
反比例函数 的图象上有两点的坐标分别为(3,a)和(2,b),a和b为了比较大小争论不休,都说自己比对方大,你能给他们评评理,到底谁比较大吗?
二、探究新知
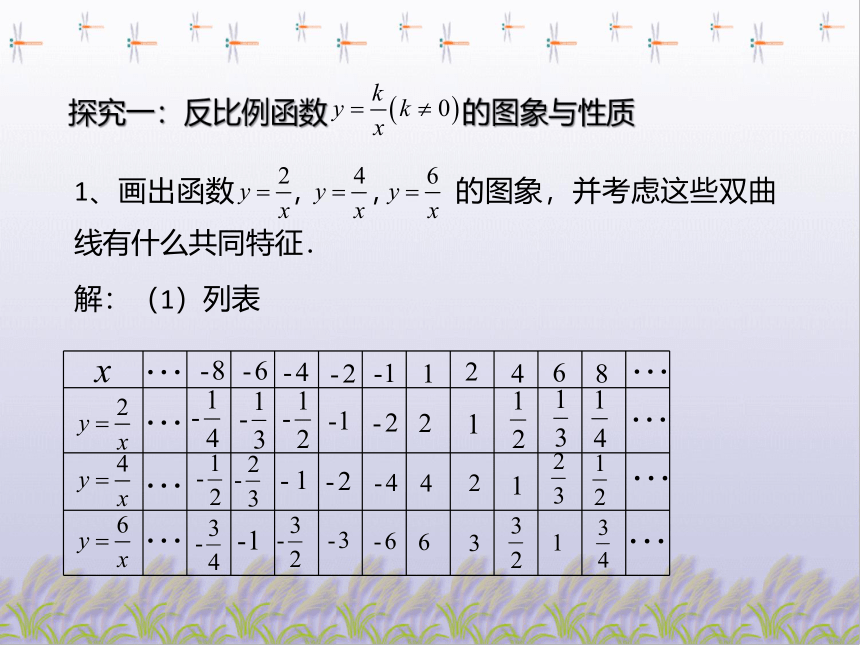
1、画出函数 , , 的图象,并考虑这些双曲线有什么共同特征.
探究一:反比例函数 的图象与性质
解:(1)列表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(2)在第一象限内,随着x值
的增大,y值是怎样变化的?
随着x值的增大,y值减小
(2):描点
(3):连线
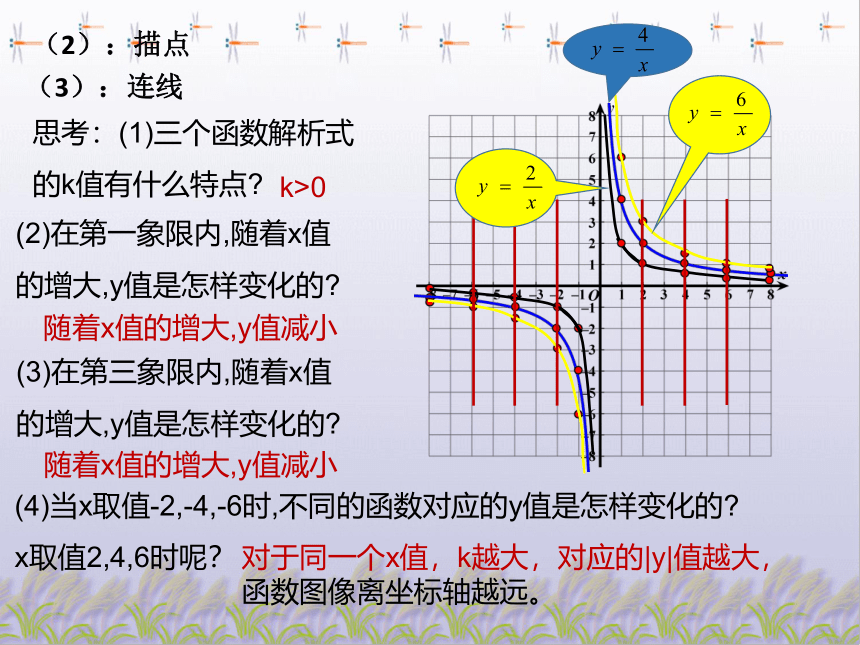
思考:(1)三个函数解析式
的k值有什么特点?
k>0
(3)在第三象限内,随着x值
的增大,y值是怎样变化的?
随着x值的增大,y值减小
(4)当x取值-2,-4,-6时,不同的函数对应的y值是怎样变化的?
x取值2,4,6时呢?
对于同一个x值,k越大,对应的|y|值越大,函数图像离坐标轴越远。
3.对于同一个x值,不同的k值,对应的y值不同. k越大,对应的|y|值越大.函数图像离坐标轴越远。
反比例函数 的图象,当k>0时,函数图象位于第一、三象限内,在每一个象限内,y的值随x值的增大而减小,k越大,对应的|y|值越大.函数图像离坐标轴越远。
1.k>0.
共同特征:
2.图象都是双曲线,都分别在第一、三象限,在每个象限内,
y随x的增大而减小.
结论:
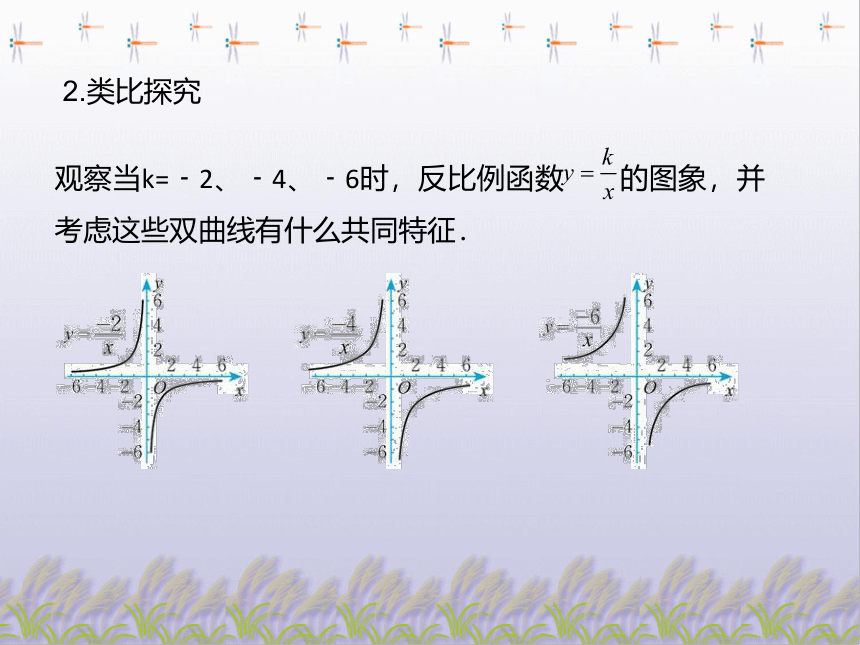
2.类比探究
观察当k=﹣2、﹣4、﹣6时,反比例函数 的图象,并考虑这些双曲线有什么共同特征.
共同特征:
2.图象都是双曲线,都分别在第二、四象限,在每个象限内,y随x的增大而增大.
结论:
反比例函数 的图象,当k<0时,函数图象位于第二、四象限内,在每一个象限内,y的值随x值的增大而减小.|k|越大,对应的|y|值越大.函数图像离坐标轴越远。
1.k<0.
3.对于同一个x值,不同的k值,对应的y值不同. |k|越大,对应的|y|值越大.函数图像离坐标轴越远。
思考:为什么要强调在“每一个象限内”?
同一个函数图象在不同的象限的点的函数值的大小不能用增减性进行判断:
对于反比例函数 ,第一象限内点的函数值始终大于第三象限内的点的函数值;
对于反比例函数 ,第二象限内点的函数值始终大于第四象限内的点的函数值.
3.归纳慨括:反比例函数 的性质是什么? 小组讨论,列表归纳:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
图像
增减性
图象与k值关系
在每一个象限内,y的值随x值的增大而减小.
在每一个象限内,y的值随x值的增大而增大.
对于同一个x值,|k|越大,对应的|y|值大,即|k|越大,图象位置相对于坐标原点越远.
思考:对于情境引入中a和b的大小比较,你的判断对吗?
当k>0时,ab.
反比例函数 的图象上有两点的坐标分别为(3,a)和(2,b),a和b为了比较大小争论不休,都说自己比对方大,你能给他们评评理,到底谁比较大吗?
(3)反比例函数 的图象上有三点的坐标分别为(3,a),(2,b)和(﹣5,c),a,b,c的大小顺序是怎样的呢?
例1.(1)已知反比例函数 的图象为于第一、三象限,求m的值.
(2)已知反比例函数 的图象在每个象限内都有y随x的增大而增大,求m的值.
解析:
(1)根据题意,得
解得m=3.
(2)根据题意,得
解得m=-2.
三、例题讲解
1.自主探究
在一个反比例函数图象任取两点A、B,过点A分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为 ;过点B分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为 , 与 有什么关系?为什么?
探究二:反比例函数 图象中的等面积矩形
因为A,B为图象上的点,
所以满足 , .
过A作AA1⊥x轴于A1,AA2⊥x轴于A2,
于是有A1(a,0),A2(0, ),
所以矩形AA1OA2的面积为 = ;
同理矩形BB1OB2的面积为 = .
故 = .
(1)对于具体的反比例函数 ,此时 与 有什么关系?为什么?
两个矩形面积相等,都等于横坐标与纵坐标绝对值的乘积.
思考:
对于反比例函数 ,有怎样的结论?
过反比例函数图象上任一点分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为:S矩=|k|.
(2)对于一般反比例函数 ,此时 与 有什么关系?为什么?
2.类比探究
在一个反比例函数图象任取点A,过点A作y轴的平行线(或作x轴的平行线),连接OA,与坐标轴围成的三角形面积为S,S有什么特点?为什么?
过反比例函数图象上任一点,作x轴或y轴的平行线,并连接该点与坐标原点,与坐标轴所围成的三角形面积为: ,即 .
探究二:反比例函数 图象中的等面积矩形
例2.如图所示,A,C是函数 的图象上任意两点,过A点作AB⊥x轴于点B,过C点作CD⊥y轴于点D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则( )
A.S1>S2 B.S1<S2
C.S1=S2 D.无法确定
解析:
因为过双曲线上任意一点与原点所连的线段、坐标轴、以及向坐标轴作垂线所围成的直角三角形面积S是个定值,且 ,所以S1=S2= .
C
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}反比例函数的图象与性质
归纳总结:
表达式
图像的形状及位置
第一三象限(x,y同号)
第二四象限(x,y异号)
增减性
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
K的几何意义
必做题:教材第157页习题6.3的1,2,3题.
选做题:教材第157页习题6.3的第4,5题.
布置作业:
第二课时
同学们还记得反比例函数图象的画法和特点吗?
一、回顾与思考
画法:
(1):列表
(2):描点
(3):连线
特点:
(1)形状:
反比例函数 的图象是由两支曲线组成的.
(2)位置:
当k>0时, 两支曲线分别位于第一、三象限;k<0时, 两支曲线分别位于第二、四象限.
(3)对称性:
反比例函数 的图象是既轴对称图形是中心对称图形,有两条对称轴,对称轴是直线y=x和y=-x;对称中心是坐标原点.
(1)列表时,选取的自变量的值,即要易于计算,又要易于描点,尽量多取点,这样使图象更精确;
(2)描点时,严格按照列表中对应值描点,不能描错.
(3)连线时,按横坐标从小到大的顺序用光滑的曲线依次连接各点,不能用折线连接.
(4)根据反比例函数自变量的取值范围可知, 图象是延伸的,且不与坐标轴相交,所以图象中不能有明确的端点,以及与坐标轴的交点.
画反比例函数图象时应注意的问题:
反比例函数 的图象上有两点的坐标分别为(3,a)和(2,b),a和b为了比较大小争论不休,都说自己比对方大,你能给他们评评理,到底谁比较大吗?
二、探究新知
1、画出函数 , , 的图象,并考虑这些双曲线有什么共同特征.
探究一:反比例函数 的图象与性质
解:(1)列表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(2)在第一象限内,随着x值
的增大,y值是怎样变化的?
随着x值的增大,y值减小
(2):描点
(3):连线
思考:(1)三个函数解析式
的k值有什么特点?
k>0
(3)在第三象限内,随着x值
的增大,y值是怎样变化的?
随着x值的增大,y值减小
(4)当x取值-2,-4,-6时,不同的函数对应的y值是怎样变化的?
x取值2,4,6时呢?
对于同一个x值,k越大,对应的|y|值越大,函数图像离坐标轴越远。
3.对于同一个x值,不同的k值,对应的y值不同. k越大,对应的|y|值越大.函数图像离坐标轴越远。
反比例函数 的图象,当k>0时,函数图象位于第一、三象限内,在每一个象限内,y的值随x值的增大而减小,k越大,对应的|y|值越大.函数图像离坐标轴越远。
1.k>0.
共同特征:
2.图象都是双曲线,都分别在第一、三象限,在每个象限内,
y随x的增大而减小.
结论:
2.类比探究
观察当k=﹣2、﹣4、﹣6时,反比例函数 的图象,并考虑这些双曲线有什么共同特征.
共同特征:
2.图象都是双曲线,都分别在第二、四象限,在每个象限内,y随x的增大而增大.
结论:
反比例函数 的图象,当k<0时,函数图象位于第二、四象限内,在每一个象限内,y的值随x值的增大而减小.|k|越大,对应的|y|值越大.函数图像离坐标轴越远。
1.k<0.
3.对于同一个x值,不同的k值,对应的y值不同. |k|越大,对应的|y|值越大.函数图像离坐标轴越远。
思考:为什么要强调在“每一个象限内”?
同一个函数图象在不同的象限的点的函数值的大小不能用增减性进行判断:
对于反比例函数 ,第一象限内点的函数值始终大于第三象限内的点的函数值;
对于反比例函数 ,第二象限内点的函数值始终大于第四象限内的点的函数值.
3.归纳慨括:反比例函数 的性质是什么? 小组讨论,列表归纳:
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
图像
增减性
图象与k值关系
在每一个象限内,y的值随x值的增大而减小.
在每一个象限内,y的值随x值的增大而增大.
对于同一个x值,|k|越大,对应的|y|值大,即|k|越大,图象位置相对于坐标原点越远.
思考:对于情境引入中a和b的大小比较,你的判断对吗?
当k>0时,a
反比例函数 的图象上有两点的坐标分别为(3,a)和(2,b),a和b为了比较大小争论不休,都说自己比对方大,你能给他们评评理,到底谁比较大吗?
(3)反比例函数 的图象上有三点的坐标分别为(3,a),(2,b)和(﹣5,c),a,b,c的大小顺序是怎样的呢?
例1.(1)已知反比例函数 的图象为于第一、三象限,求m的值.
(2)已知反比例函数 的图象在每个象限内都有y随x的增大而增大,求m的值.
解析:
(1)根据题意,得
解得m=3.
(2)根据题意,得
解得m=-2.
三、例题讲解
1.自主探究
在一个反比例函数图象任取两点A、B,过点A分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为 ;过点B分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为 , 与 有什么关系?为什么?
探究二:反比例函数 图象中的等面积矩形
因为A,B为图象上的点,
所以满足 , .
过A作AA1⊥x轴于A1,AA2⊥x轴于A2,
于是有A1(a,0),A2(0, ),
所以矩形AA1OA2的面积为 = ;
同理矩形BB1OB2的面积为 = .
故 = .
(1)对于具体的反比例函数 ,此时 与 有什么关系?为什么?
两个矩形面积相等,都等于横坐标与纵坐标绝对值的乘积.
思考:
对于反比例函数 ,有怎样的结论?
过反比例函数图象上任一点分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为:S矩=|k|.
(2)对于一般反比例函数 ,此时 与 有什么关系?为什么?
2.类比探究
在一个反比例函数图象任取点A,过点A作y轴的平行线(或作x轴的平行线),连接OA,与坐标轴围成的三角形面积为S,S有什么特点?为什么?
过反比例函数图象上任一点,作x轴或y轴的平行线,并连接该点与坐标原点,与坐标轴所围成的三角形面积为: ,即 .
探究二:反比例函数 图象中的等面积矩形
例2.如图所示,A,C是函数 的图象上任意两点,过A点作AB⊥x轴于点B,过C点作CD⊥y轴于点D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则( )
A.S1>S2 B.S1<S2
C.S1=S2 D.无法确定
解析:
因为过双曲线上任意一点与原点所连的线段、坐标轴、以及向坐标轴作垂线所围成的直角三角形面积S是个定值,且 ,所以S1=S2= .
C
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}反比例函数的图象与性质
归纳总结:
表达式
图像的形状及位置
第一三象限(x,y同号)
第二四象限(x,y异号)
增减性
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
K的几何意义
必做题:教材第157页习题6.3的1,2,3题.
选做题:教材第157页习题6.3的第4,5题.
布置作业:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
