第16章轴对称和中心对称复习与小结-冀教版八年级数学上册课件(共27张ppt)
文档属性
| 名称 | 第16章轴对称和中心对称复习与小结-冀教版八年级数学上册课件(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览






文档简介
复习与小结
第十六章 轴对称和中心对称
冀教版八上
学习目标
冀教版八上
1.感受轴对称、中心对称的概念、性质及其应用.
2.掌握线段中垂线、角平分线的性质定理及其逆定理.
3.培养举一反三、由浅入深的良好思维习惯.
知识回顾
一、轴对称和中心对称
1.轴对称图形
轴对称图形
对称轴
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做_____________,这条直线叫做_______.
知识回顾
一、轴对称和中心对称
2.轴对称的性质
如果两个图形关于某条直线成轴对称,那么,这两个图形是________,它们的_______________,_____________,对应点所连的线段被对称轴垂直平分.
全等形
对应线段相等
对应角相等
知识回顾
一、轴对称和中心对称
如果一个图形绕一个点旋转_____后,能和原来的图形互相重合,那么这个图形叫做_______________;这个点叫做它的___________;互相重合的点叫做_______.
3.中心对称图形
180°
中心对称图形
对称中心
对称点
知识回顾
一、轴对称和中心对称
4.中心对称的性质
如果两个图形成中心对称,那么,这两个图形是________,它们的_______________,_____________,对应点的连线经过对称中心,并且被对称中心平分.
全等形
对应线段相等
对应角相等
知识运用
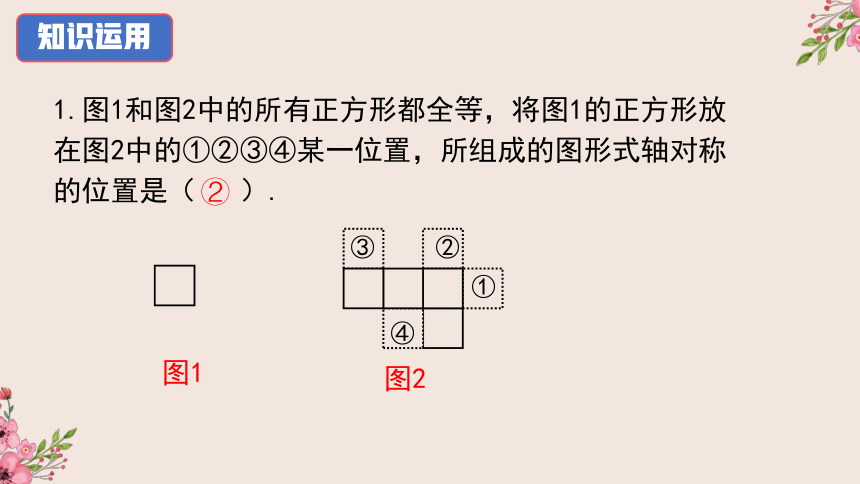
1.图1和图2中的所有正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形式轴对称的位置是( ).
图1
①
②
③
④
图2
②
知识运用
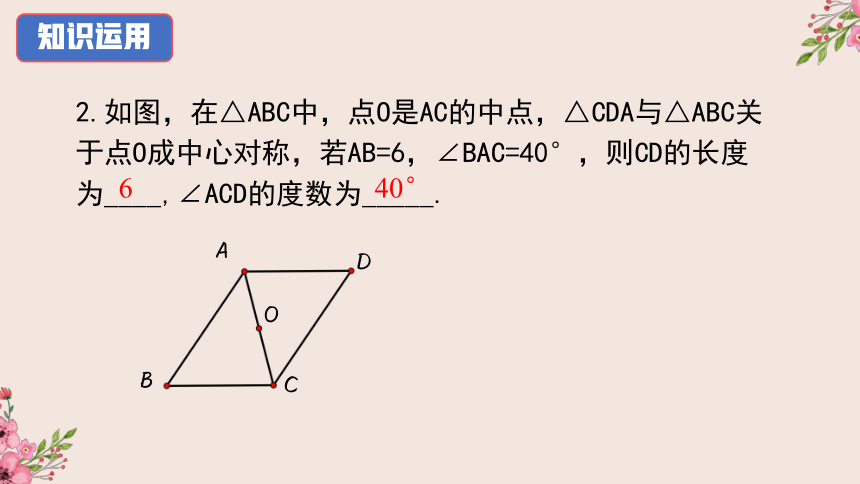
2.如图,在△ABC中,点O是AC的中点,△CDA与△ABC关于点O成中心对称,若AB=6,∠BAC=40°,则CD的长度为____,∠ACD的度数为_____.
O
D
A
C
B
6
40°
知识运用
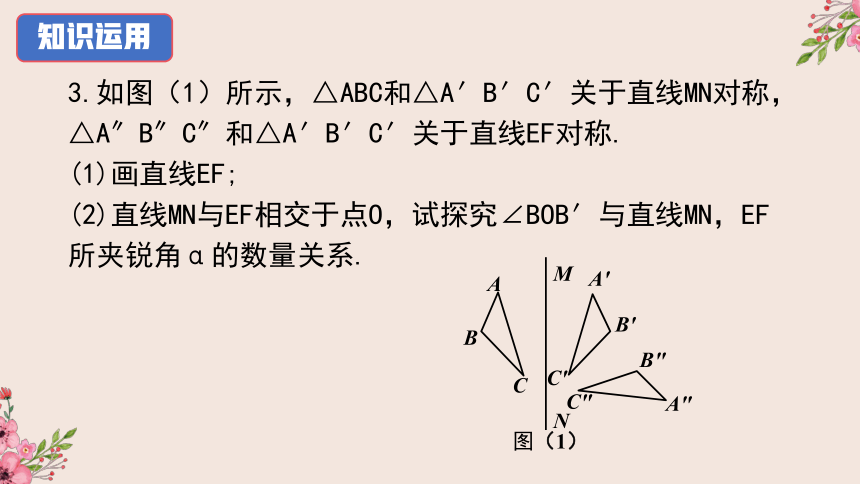
3.如图(1)所示,△ABC和△A′B′C′关于直线MN对称,△A″B″C″和△A′B′C′关于直线EF对称.
(1)画直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB′与直线MN,EF所夹锐角α的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
图(1)
M
N
知识运用
分析:本题考查的是对称轴的画法及轴对称的性质,连接△A′B′C′和△A″B″C″中的任意一对对应点,作所得线段的垂直平分线即为直线EF,根据轴对称的性质可求角的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
图(1)
M
N
知识运用
A
B
C
A′
B′
C′
A″
B″
C″
图(2)
答案:(1)如图(2)所示,连接B ′ B ″,作线段B ′ B ″的垂直平分线EF,则直线EF是△A ′ B ′ C ′和△A ″ B ″ C ″的对称轴.
(2)连接B″O,B′O,BO,
∵ △ABC和△A′B′C′关于直线MN对称,
∴ ∠BOM=∠B'OM.
∵ △A''B''C''和△A'B'C'关于直线EF对称,
∴ ∠B'OE= ∠B''OE.
∴ ∠B'OB''= 2(∠B'OM+ ∠B'OE)=2α.
E
F
O
M
N
知识回顾
二、线段的垂直平分线的性质定理及其逆定理
1.线段的垂直平分线
_____________一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
垂直且平分
知识回顾
线段垂直平分线上的点到线段两个端点的距离相等.
2.线段垂直平分线的性质定理
二、线段的垂直平分线的性质定理及其逆定理
用途:
用于证明两条线段相等.
常用辅助线:
连接点与线段的两个端点.
知识回顾
3.线段垂直平分线的性质定理的逆定理
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、线段的垂直平分线的性质定理及其逆定理
用途:
判断点是否在某线段的中垂线上.
用两个点可以判定线段的中垂线.
知识回顾
4.三角形的三边中垂线的有关结论
三角形的三条边的中垂线相交于一点.
二、线段的垂直平分线的性质定理及其逆定理
这个点到三角形三个顶点的距离相等.
知识运用
1.如图,已知AC-BC=3,AB的垂直平分线分别AB,AC于点D,E,△BCE的周长是15,则AC的长为______.
E
D
A
C
B
注意:
当已知条件中出现线段的中垂线时,一般要考虑用线段中垂线的性质定理.
9
知识运用
2.如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,则线段QR的长为______.
M
O
A
N
B
R
Q
P
4.5cm
知识点:
对称轴是对应点连线的垂直平分线.
知识回顾
三、角平分线的性质定理及其逆定理
1.角平分线的性质定理
角的平分线上的点到角的两边的距离相等.
用途:
证明两条垂线段相等.
常用辅助线:
作点到角两边的距离.
知识回顾
三、角平分线的性质定理及其逆定理
2.角平分线性质定理的逆定理
到角的两边距离相等的点在角的平分线上.
用途:
判定角平分线.
3.三角形的三内角平分线的有关结论
三角形的三个内角的平分线交于一点,这个点到
三角形三边的距离相等.
知识运用
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为_____.
M
O
A
N
Q
P
知识点:
①垂线段最短
②角平分线的性质定理
2
知识运用
2.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
则求DE的长为_____.△ADB的面积为_____.
E
D
A
C
B
3
15
知识运用
3.如图,∠MON=90°,OM是∠AOB的平分线,使三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D.则PC和PD有怎样的数量关系?证明你的结论.
M
C
A
O
B
P
D
辅助线:
做出点P到∠AOB两边的距离,构造出角平分线性质定理的基本图形.
知识运用
M
C
A
O
B
P
D
解:PC=PD.
理由:过点P分别作PE⊥OB于点E,PF⊥OA于点F.
∵OM平分∠ABO,PE⊥OB,PF⊥OA
∴PE=PF
∵∠CPF+∠FPD=90°,∠DPE+∠FPD=90°
∴∠CPF=∠DPE
又∠CFP=∠DEP=90°
∴△CFP≌△DEP
∴PC=PD
E
F
题中有多个直角时,要考虑用同角的余角相等
知识回顾
四、图案的设计
图形的变换可以通过选择不同的变换方式得到,可能需要_______、_______、_______等多种变换组合才能得到完美的图案.
旋转
轴对称
平移
知识运用
如图,在正方形网格在,阴影部分是涂黑的7个小正方形所形成的图案,再将网格空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有____种.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3
课堂小结
轴对称
轴对称图形
性质
线段
角
线段垂直平分线的性质定理和它的逆定理
角平分线的性质定理和它的逆定理
概念
两个图形成轴对称
成轴对称的两个图形中,对应线段相等,对应角相等,对应点连线被对称轴垂直平分
中心对称
性质
概念
中心称图形
两个图形成中心对称
成中心对称的两个图形中,对应点的连线经过对称中心,并且被对称中心平分
利用图形的平移、旋转和轴对称设计图案
同学们再见
第十六章 轴对称和中心对称
冀教版八上
学习目标
冀教版八上
1.感受轴对称、中心对称的概念、性质及其应用.
2.掌握线段中垂线、角平分线的性质定理及其逆定理.
3.培养举一反三、由浅入深的良好思维习惯.
知识回顾
一、轴对称和中心对称
1.轴对称图形
轴对称图形
对称轴
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做_____________,这条直线叫做_______.
知识回顾
一、轴对称和中心对称
2.轴对称的性质
如果两个图形关于某条直线成轴对称,那么,这两个图形是________,它们的_______________,_____________,对应点所连的线段被对称轴垂直平分.
全等形
对应线段相等
对应角相等
知识回顾
一、轴对称和中心对称
如果一个图形绕一个点旋转_____后,能和原来的图形互相重合,那么这个图形叫做_______________;这个点叫做它的___________;互相重合的点叫做_______.
3.中心对称图形
180°
中心对称图形
对称中心
对称点
知识回顾
一、轴对称和中心对称
4.中心对称的性质
如果两个图形成中心对称,那么,这两个图形是________,它们的_______________,_____________,对应点的连线经过对称中心,并且被对称中心平分.
全等形
对应线段相等
对应角相等
知识运用
1.图1和图2中的所有正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形式轴对称的位置是( ).
图1
①
②
③
④
图2
②
知识运用
2.如图,在△ABC中,点O是AC的中点,△CDA与△ABC关于点O成中心对称,若AB=6,∠BAC=40°,则CD的长度为____,∠ACD的度数为_____.
O
D
A
C
B
6
40°
知识运用
3.如图(1)所示,△ABC和△A′B′C′关于直线MN对称,△A″B″C″和△A′B′C′关于直线EF对称.
(1)画直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB′与直线MN,EF所夹锐角α的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
图(1)
M
N
知识运用
分析:本题考查的是对称轴的画法及轴对称的性质,连接△A′B′C′和△A″B″C″中的任意一对对应点,作所得线段的垂直平分线即为直线EF,根据轴对称的性质可求角的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
图(1)
M
N
知识运用
A
B
C
A′
B′
C′
A″
B″
C″
图(2)
答案:(1)如图(2)所示,连接B ′ B ″,作线段B ′ B ″的垂直平分线EF,则直线EF是△A ′ B ′ C ′和△A ″ B ″ C ″的对称轴.
(2)连接B″O,B′O,BO,
∵ △ABC和△A′B′C′关于直线MN对称,
∴ ∠BOM=∠B'OM.
∵ △A''B''C''和△A'B'C'关于直线EF对称,
∴ ∠B'OE= ∠B''OE.
∴ ∠B'OB''= 2(∠B'OM+ ∠B'OE)=2α.
E
F
O
M
N
知识回顾
二、线段的垂直平分线的性质定理及其逆定理
1.线段的垂直平分线
_____________一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
垂直且平分
知识回顾
线段垂直平分线上的点到线段两个端点的距离相等.
2.线段垂直平分线的性质定理
二、线段的垂直平分线的性质定理及其逆定理
用途:
用于证明两条线段相等.
常用辅助线:
连接点与线段的两个端点.
知识回顾
3.线段垂直平分线的性质定理的逆定理
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、线段的垂直平分线的性质定理及其逆定理
用途:
判断点是否在某线段的中垂线上.
用两个点可以判定线段的中垂线.
知识回顾
4.三角形的三边中垂线的有关结论
三角形的三条边的中垂线相交于一点.
二、线段的垂直平分线的性质定理及其逆定理
这个点到三角形三个顶点的距离相等.
知识运用
1.如图,已知AC-BC=3,AB的垂直平分线分别AB,AC于点D,E,△BCE的周长是15,则AC的长为______.
E
D
A
C
B
注意:
当已知条件中出现线段的中垂线时,一般要考虑用线段中垂线的性质定理.
9
知识运用
2.如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,则线段QR的长为______.
M
O
A
N
B
R
Q
P
4.5cm
知识点:
对称轴是对应点连线的垂直平分线.
知识回顾
三、角平分线的性质定理及其逆定理
1.角平分线的性质定理
角的平分线上的点到角的两边的距离相等.
用途:
证明两条垂线段相等.
常用辅助线:
作点到角两边的距离.
知识回顾
三、角平分线的性质定理及其逆定理
2.角平分线性质定理的逆定理
到角的两边距离相等的点在角的平分线上.
用途:
判定角平分线.
3.三角形的三内角平分线的有关结论
三角形的三个内角的平分线交于一点,这个点到
三角形三边的距离相等.
知识运用
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为_____.
M
O
A
N
Q
P
知识点:
①垂线段最短
②角平分线的性质定理
2
知识运用
2.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
则求DE的长为_____.△ADB的面积为_____.
E
D
A
C
B
3
15
知识运用
3.如图,∠MON=90°,OM是∠AOB的平分线,使三角板的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D.则PC和PD有怎样的数量关系?证明你的结论.
M
C
A
O
B
P
D
辅助线:
做出点P到∠AOB两边的距离,构造出角平分线性质定理的基本图形.
知识运用
M
C
A
O
B
P
D
解:PC=PD.
理由:过点P分别作PE⊥OB于点E,PF⊥OA于点F.
∵OM平分∠ABO,PE⊥OB,PF⊥OA
∴PE=PF
∵∠CPF+∠FPD=90°,∠DPE+∠FPD=90°
∴∠CPF=∠DPE
又∠CFP=∠DEP=90°
∴△CFP≌△DEP
∴PC=PD
E
F
题中有多个直角时,要考虑用同角的余角相等
知识回顾
四、图案的设计
图形的变换可以通过选择不同的变换方式得到,可能需要_______、_______、_______等多种变换组合才能得到完美的图案.
旋转
轴对称
平移
知识运用
如图,在正方形网格在,阴影部分是涂黑的7个小正方形所形成的图案,再将网格空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有____种.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3
课堂小结
轴对称
轴对称图形
性质
线段
角
线段垂直平分线的性质定理和它的逆定理
角平分线的性质定理和它的逆定理
概念
两个图形成轴对称
成轴对称的两个图形中,对应线段相等,对应角相等,对应点连线被对称轴垂直平分
中心对称
性质
概念
中心称图形
两个图形成中心对称
成中心对称的两个图形中,对应点的连线经过对称中心,并且被对称中心平分
利用图形的平移、旋转和轴对称设计图案
同学们再见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
