沪科版数学 八年级上册14.2.5直角三角形全等的判定(共17张ppt)
文档属性
| 名称 | 沪科版数学 八年级上册14.2.5直角三角形全等的判定(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 558.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览




文档简介
沪科版 八年级上册
14.2.5直角三角形全等的判定 (HL)
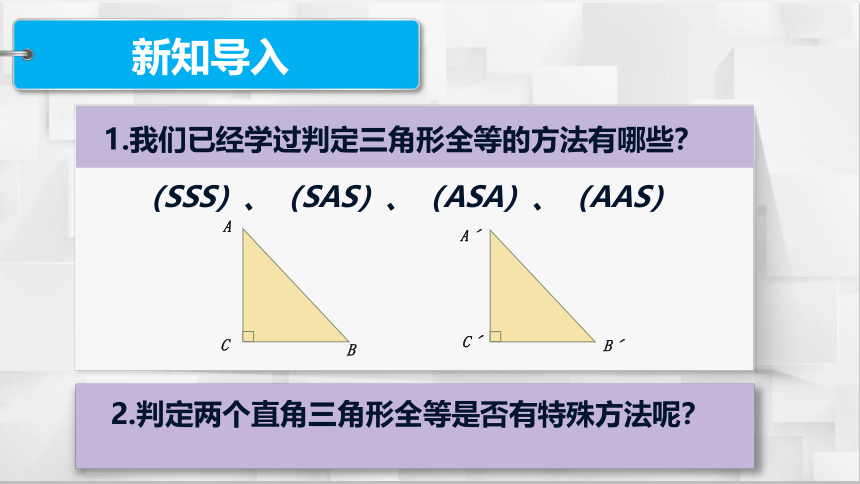
新知导入
1.我们已经学过判定三角形全等的方法有哪些?
(SSS)、(SAS)、(ASA)、(AAS)
A
B
C
Aˊ
Cˊ
Bˊ
2.判定两个直角三角形全等是否有特殊方法呢?
14.2.5直角三角形全等的判定 (HL)
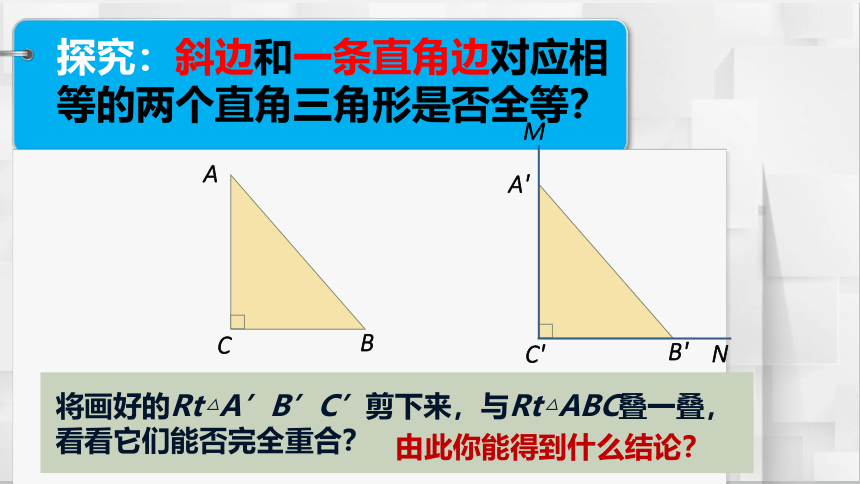
探究:斜边和一条直角边对应相等的两个直角三角形是否全等?
已知:Rt△ABC,其中∠C 为直角.
求作:Rt△A'B'C',使∠C' 为直角,
A'C'=AC,A'B'=AB.
A
B
C
探究:斜边和一条直角边对应相等的两个直角三角形是否全等?
A
B
C
A'
B'
C'
M
N
将画好的Rt△A’B’C’剪下来,与Rt△ABC叠一叠,看看它们能否完全重合?
由此你能得到什么结论?
新知讲解
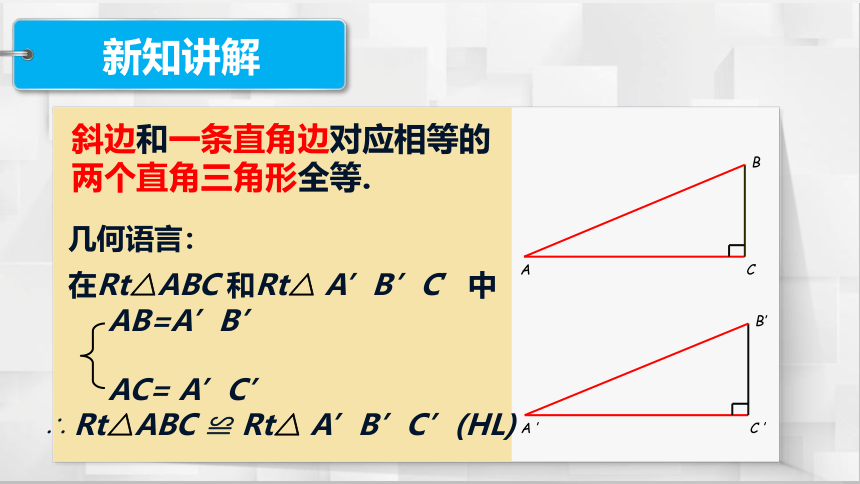
直角三角形全等的判定定理
斜边、直角边定理
简记为“斜边、直角边”或“HL”.
斜边和一条直角边对应相等的
两个直角三角形全等.
新知讲解
在Rt△ABC 和Rt△ A’B’C’中
AB=A’B’
AC= A’C’
∴ Rt△ABC ≌ Rt△ A’B’C’(HL)
几何语言:
A
B
C
A ′
B′
C ′
斜边和一条直角边对应相等的两个直角三角形全等.
直角三角形全等的判定
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
“ SSS ”
灵活运用各种方法证明直角三角形全等
典例剖析
例7:如图,∠BAC=∠CDB=90°, AC﹦DB,求证:AB﹦DC
B
C
D
A
证明: ∵∠BAC=∠CDB=90°(已知)
∴ΔBAC,ΔCDB 都是直角三角形.
在 Rt△ABC 和 Rt△DCB 中,
AC=DB(已知)
BC=CB(公共边)
∴Rt△ABC≌Rt△DCB (HL).
∴ AB﹦DC(全等三角形对应边相等)
变式训练
如图,∠BAC=∠CDB=90°,请你再添加一个条件使△ABC≌△DCB ,并说明判定依据?
1.AB=DC (HL)
2.AC=DB (HL)
3.∠ABC=∠DCB (AAS)
4.∠ACB=∠DBC (AAS)
B
C
D
A
A.SAS B.ASA C.AAS D.HL
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则判定△ABC≌△DEF 的依据是( )
A.SAS B.ASA C.AAS D.HL
试一试
2.如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=( )
A.60° B. 50° C. 40° D. 30°
B
A
C
D
E
F
D
A
练 习
已知:如图,AC⊥BD于点O,且OA=OC,AB=CD.
求证:∠B=∠D
A
B
C
D
O
证明:∵ AC⊥BD于点O,
∴∠AOB=∠DOC=90°
∴△AOB 和△COD 都是直角三角形
在Rt△AOB 和Rt△COD中
∵ OA=OC,AB=CD.
∴Rt△AOB≌Rt△COD
∴∠B=∠D
A
B
C
D
O
练 习
练 习
2.如图,两根长相等的绳子,一端都系在旗杆上的A点,另一端分别固定在地面的两个木桩上,两根木桩到旗杆底部的距离相等吗?请说明理由.????
解:相等,理由如下:
在Rt△ABO 和Rt△ACO 中,
∵AB=AC,AO=AO,∴Rt△ABO≌Rt△ACO(HL),∴OB=OC.
即两根木桩到旗杆底部的距离相等.
课堂总结
这节课我们学了什么?
作业布置
必做题:习题14.2第10题
选做题: 同步P88页当堂检测
谢
谢
聆
听
14.2.5直角三角形全等的判定 (HL)
新知导入
1.我们已经学过判定三角形全等的方法有哪些?
(SSS)、(SAS)、(ASA)、(AAS)
A
B
C
Aˊ
Cˊ
Bˊ
2.判定两个直角三角形全等是否有特殊方法呢?
14.2.5直角三角形全等的判定 (HL)
探究:斜边和一条直角边对应相等的两个直角三角形是否全等?
已知:Rt△ABC,其中∠C 为直角.
求作:Rt△A'B'C',使∠C' 为直角,
A'C'=AC,A'B'=AB.
A
B
C
探究:斜边和一条直角边对应相等的两个直角三角形是否全等?
A
B
C
A'
B'
C'
M
N
将画好的Rt△A’B’C’剪下来,与Rt△ABC叠一叠,看看它们能否完全重合?
由此你能得到什么结论?
新知讲解
直角三角形全等的判定定理
斜边、直角边定理
简记为“斜边、直角边”或“HL”.
斜边和一条直角边对应相等的
两个直角三角形全等.
新知讲解
在Rt△ABC 和Rt△ A’B’C’中
AB=A’B’
AC= A’C’
∴ Rt△ABC ≌ Rt△ A’B’C’(HL)
几何语言:
A
B
C
A ′
B′
C ′
斜边和一条直角边对应相等的两个直角三角形全等.
直角三角形全等的判定
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
“ SSS ”
灵活运用各种方法证明直角三角形全等
典例剖析
例7:如图,∠BAC=∠CDB=90°, AC﹦DB,求证:AB﹦DC
B
C
D
A
证明: ∵∠BAC=∠CDB=90°(已知)
∴ΔBAC,ΔCDB 都是直角三角形.
在 Rt△ABC 和 Rt△DCB 中,
AC=DB(已知)
BC=CB(公共边)
∴Rt△ABC≌Rt△DCB (HL).
∴ AB﹦DC(全等三角形对应边相等)
变式训练
如图,∠BAC=∠CDB=90°,请你再添加一个条件使△ABC≌△DCB ,并说明判定依据?
1.AB=DC (HL)
2.AC=DB (HL)
3.∠ABC=∠DCB (AAS)
4.∠ACB=∠DBC (AAS)
B
C
D
A
A.SAS B.ASA C.AAS D.HL
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则判定△ABC≌△DEF 的依据是( )
A.SAS B.ASA C.AAS D.HL
试一试
2.如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=( )
A.60° B. 50° C. 40° D. 30°
B
A
C
D
E
F
D
A
练 习
已知:如图,AC⊥BD于点O,且OA=OC,AB=CD.
求证:∠B=∠D
A
B
C
D
O
证明:∵ AC⊥BD于点O,
∴∠AOB=∠DOC=90°
∴△AOB 和△COD 都是直角三角形
在Rt△AOB 和Rt△COD中
∵ OA=OC,AB=CD.
∴Rt△AOB≌Rt△COD
∴∠B=∠D
A
B
C
D
O
练 习
练 习
2.如图,两根长相等的绳子,一端都系在旗杆上的A点,另一端分别固定在地面的两个木桩上,两根木桩到旗杆底部的距离相等吗?请说明理由.????
解:相等,理由如下:
在Rt△ABO 和Rt△ACO 中,
∵AB=AC,AO=AO,∴Rt△ABO≌Rt△ACO(HL),∴OB=OC.
即两根木桩到旗杆底部的距离相等.
课堂总结
这节课我们学了什么?
作业布置
必做题:习题14.2第10题
选做题: 同步P88页当堂检测
谢
谢
聆
听
