华东师大版数学八年级上册-14.1.2 直角三角形判定 课件(共16张ppt)
文档属性
| 名称 | 华东师大版数学八年级上册-14.1.2 直角三角形判定 课件(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 702.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 11:42:17 | ||
图片预览





文档简介
直角三角形的判定
1.直角三角形有哪些性质?(从边、角两方面考虑)
(1)有一个角是直角;
(2)两个锐角的和为90°(互余 );
(3)两直角边的平方和等于斜边的平方 .
反之,一个三角形满足什么条件
才能是直角三角形呢?
忆一忆
(即勾股定理)
请用数学符号表示勾股定理
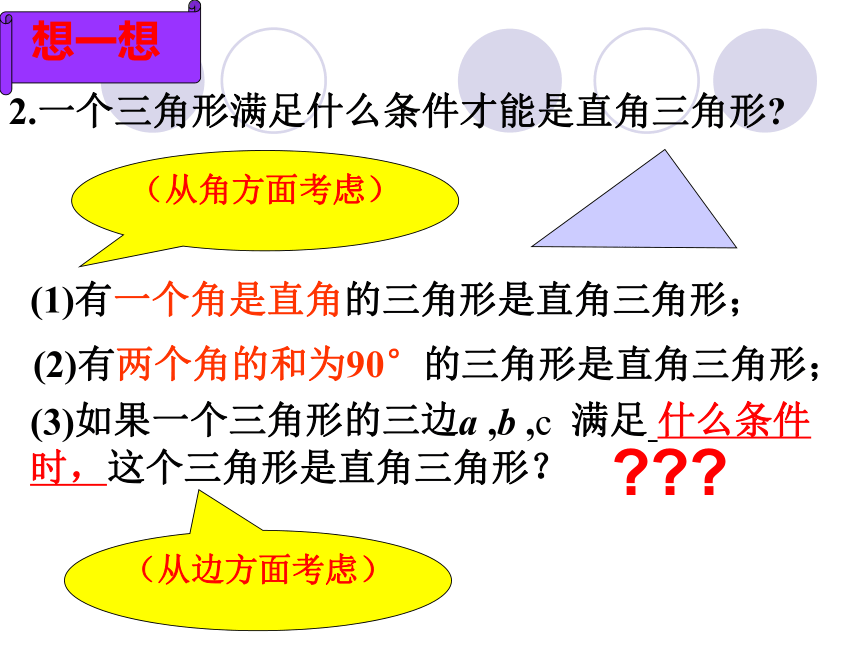
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和为90°的三角形是直角三角形;
(3)如果一个三角形的三边a ,b ,c 满足 什么条件时,这个三角形是直角三角形?
2.一个三角形满足什么条件才能是直角三角形?
想一想
???
(从角方面考虑)
(从边方面考虑)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
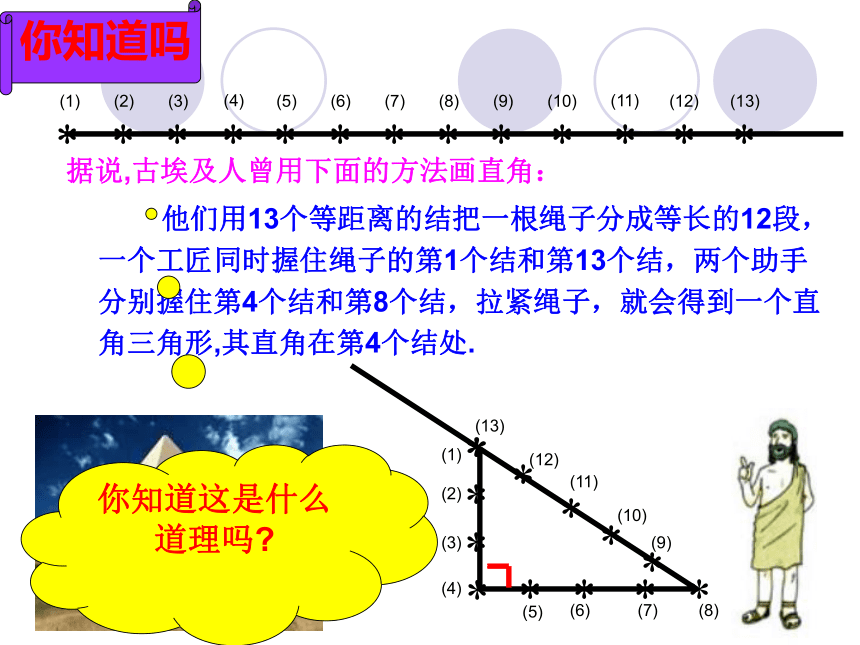
据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
你知道吗
你知道这是什么道理吗?
活动1:请三个同学上台演示古埃及人画直角的方法
活动2:请一个同学上台测量所得的三角形最大的角的度数
想一想:这个同学量得的最大角是什么类型的角?所以所得的三角形是什么三角形?你知道这是什么道理吗?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
二、合作探究,发现新知
1.试画出三边长度分别为如下数据的三角形,并把所画出来的的三角形剪下来备用。(小组合作,每个小组成员各剪一个三角形)
(1)a=6,b=4,c=5; (2)a=6,b=8,c=10;
(3)a=4,b=6,c=8; (4)a=5,b=12,c=13;
(课前画好三角形,三边标注数值,并剪下备用)
活动1:请同学们拿出已剪好的三角形卡片,按四个同学一组座位坐好。
(1)a=6,b=4,c=5; (2)a=6,b=8,c=10;
(3)a=4,b=6,c=8; (4)a=5,b=12,c=13;
2. 观察你所画的三角形,并用量角器量一量最长边所对角的度数,判断其角的形状。
(1) 角;(2) 角;
(3) 角 ;(4) 角。
活动2:测量手中的三角形最大角的度数,并判断其角的类型。(在卡片中标注),小组成员互相交流
二、合作探究,发现新知
3.按要求填表(小组合作完成)
学生活动3:
活动4:请小组代表上台展示卡片,并给出计算过程,
并判断你手中的三角形是否是直角三角形。
(请比较上述每个三角形的两条较短边的平方和与最长边的平方
之间的大小关系,最长边所对的角是什么形状)
4.通过以上探究,你发现一个三角形的三边满足什么
条件是直角三角形?
猜想:
如果三角形的三边长a、b、c满足a2+b2=c2,
那么这个三角形是直角三角形,且c所对的角是
直角三角形。
如何证明这个命题的正确性?
如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形.
a2 + b2 = c2
反过来
知识要点
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 .
a2 + b2 = c2
勾股定理的逆定理:
用来判定一个三角形是直角三角形,或判定一个角是直角
例1 判断由线段a,b,c组成的三角形是不是直角三角形?若是指出哪个角是直角。
(1)a=, ,b=2,c=1;
(2)a=13,b=9,c=11;
(3)a=3,b=4,c=5
根据勾股定理的逆定理,判断一个三角形是否是直角三角形的步骤:
(1)找出最长边;
(2)看两条较短的边的平方和是否等于最长的边的平方。如果相等,则是,最长边对直角; 如果不相等,则不是。
勾股数:
能够成为直角三角形三条边的三个正整数,称为勾股数
例2 一个零件的形状如下左图所示,按照规定这个零件中∠A 和∠DBC都是直角.量得各边尺寸如图所示,这零件符合要求吗?并说明理由。
分析:由题意,本题只需证明∠A 和∠DBC都是直角即可。如何证明一个角是直角呢?
用勾股定理的逆定理证明
解:如图,设每两个结的 距离为a(a>0),则AC=3a,BC=4a,AB=5a.
原来如此
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
A
B
C
例3 解释“古埃及人画直角”的理论根据
(四)随堂练习,巩固深化
1.下列各组数中,是勾股数的是( )
A. 5 ,6, 7 B. ,3,1
C. 8,10, 6 D. 3,3,4
2.在△ABC中,若a=5,b=3,c=4,则△ABC是
( )三角形.
A.锐角 B.直角 C.钝角 D.无法确定
3. 满足下列条件△ABC,不是直角三角形的是( )
A.b2 = a2 -c2 B . a∶b∶c=3∶4∶5
C. ∠C=∠A-∠B D .∠A∶∠B ∶∠C=3∶4∶5
4. 已知:在△ABC 中,AB=12,BC=9,AC=15,
求证:△ABC是直角三角形
5.选做(智力大冲浪)三角形三边长a, b, c满足条件:(a+b)2-c2=2ab,则此三角形是( )
A. 锐角三角形 B. 直角三角形
C.钝角三角形 D. 等边三角形
6.中考链接(选做)
小明画了一个如上右图所示的四边形,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
A
B
C
D
通过本节课的学习,我们知道了:
1、 勾股定理的逆定理的内容;
2、判定一个三角形是直角三角形的方法(从角、边两个方面来考虑);
3、勾股定理与它的逆定理之间的关系.
4、数形结合的数学思想.
课堂小结
真诚致意
感谢各位同学精彩配合!
1.直角三角形有哪些性质?(从边、角两方面考虑)
(1)有一个角是直角;
(2)两个锐角的和为90°(互余 );
(3)两直角边的平方和等于斜边的平方 .
反之,一个三角形满足什么条件
才能是直角三角形呢?
忆一忆
(即勾股定理)
请用数学符号表示勾股定理
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和为90°的三角形是直角三角形;
(3)如果一个三角形的三边a ,b ,c 满足 什么条件时,这个三角形是直角三角形?
2.一个三角形满足什么条件才能是直角三角形?
想一想
???
(从角方面考虑)
(从边方面考虑)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
你知道吗
你知道这是什么道理吗?
活动1:请三个同学上台演示古埃及人画直角的方法
活动2:请一个同学上台测量所得的三角形最大的角的度数
想一想:这个同学量得的最大角是什么类型的角?所以所得的三角形是什么三角形?你知道这是什么道理吗?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
二、合作探究,发现新知
1.试画出三边长度分别为如下数据的三角形,并把所画出来的的三角形剪下来备用。(小组合作,每个小组成员各剪一个三角形)
(1)a=6,b=4,c=5; (2)a=6,b=8,c=10;
(3)a=4,b=6,c=8; (4)a=5,b=12,c=13;
(课前画好三角形,三边标注数值,并剪下备用)
活动1:请同学们拿出已剪好的三角形卡片,按四个同学一组座位坐好。
(1)a=6,b=4,c=5; (2)a=6,b=8,c=10;
(3)a=4,b=6,c=8; (4)a=5,b=12,c=13;
2. 观察你所画的三角形,并用量角器量一量最长边所对角的度数,判断其角的形状。
(1) 角;(2) 角;
(3) 角 ;(4) 角。
活动2:测量手中的三角形最大角的度数,并判断其角的类型。(在卡片中标注),小组成员互相交流
二、合作探究,发现新知
3.按要求填表(小组合作完成)
学生活动3:
活动4:请小组代表上台展示卡片,并给出计算过程,
并判断你手中的三角形是否是直角三角形。
(请比较上述每个三角形的两条较短边的平方和与最长边的平方
之间的大小关系,最长边所对的角是什么形状)
4.通过以上探究,你发现一个三角形的三边满足什么
条件是直角三角形?
猜想:
如果三角形的三边长a、b、c满足a2+b2=c2,
那么这个三角形是直角三角形,且c所对的角是
直角三角形。
如何证明这个命题的正确性?
如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形.
a2 + b2 = c2
反过来
知识要点
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 .
a2 + b2 = c2
勾股定理的逆定理:
用来判定一个三角形是直角三角形,或判定一个角是直角
例1 判断由线段a,b,c组成的三角形是不是直角三角形?若是指出哪个角是直角。
(1)a=, ,b=2,c=1;
(2)a=13,b=9,c=11;
(3)a=3,b=4,c=5
根据勾股定理的逆定理,判断一个三角形是否是直角三角形的步骤:
(1)找出最长边;
(2)看两条较短的边的平方和是否等于最长的边的平方。如果相等,则是,最长边对直角; 如果不相等,则不是。
勾股数:
能够成为直角三角形三条边的三个正整数,称为勾股数
例2 一个零件的形状如下左图所示,按照规定这个零件中∠A 和∠DBC都是直角.量得各边尺寸如图所示,这零件符合要求吗?并说明理由。
分析:由题意,本题只需证明∠A 和∠DBC都是直角即可。如何证明一个角是直角呢?
用勾股定理的逆定理证明
解:如图,设每两个结的 距离为a(a>0),则AC=3a,BC=4a,AB=5a.
原来如此
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
A
B
C
例3 解释“古埃及人画直角”的理论根据
(四)随堂练习,巩固深化
1.下列各组数中,是勾股数的是( )
A. 5 ,6, 7 B. ,3,1
C. 8,10, 6 D. 3,3,4
2.在△ABC中,若a=5,b=3,c=4,则△ABC是
( )三角形.
A.锐角 B.直角 C.钝角 D.无法确定
3. 满足下列条件△ABC,不是直角三角形的是( )
A.b2 = a2 -c2 B . a∶b∶c=3∶4∶5
C. ∠C=∠A-∠B D .∠A∶∠B ∶∠C=3∶4∶5
4. 已知:在△ABC 中,AB=12,BC=9,AC=15,
求证:△ABC是直角三角形
5.选做(智力大冲浪)三角形三边长a, b, c满足条件:(a+b)2-c2=2ab,则此三角形是( )
A. 锐角三角形 B. 直角三角形
C.钝角三角形 D. 等边三角形
6.中考链接(选做)
小明画了一个如上右图所示的四边形,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
A
B
C
D
通过本节课的学习,我们知道了:
1、 勾股定理的逆定理的内容;
2、判定一个三角形是直角三角形的方法(从角、边两个方面来考虑);
3、勾股定理与它的逆定理之间的关系.
4、数形结合的数学思想.
课堂小结
真诚致意
感谢各位同学精彩配合!
