人教版八年级上册14.1.4 整式乘法 多项式乘多项式课件(共25张ppt)
文档属性
| 名称 | 人教版八年级上册14.1.4 整式乘法 多项式乘多项式课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 11:53:46 | ||
图片预览






文档简介
14.1.4整式乘法
—多项式乘多项式
人教版 八年级 上册
m
n
a
b
bn
bm
am
an
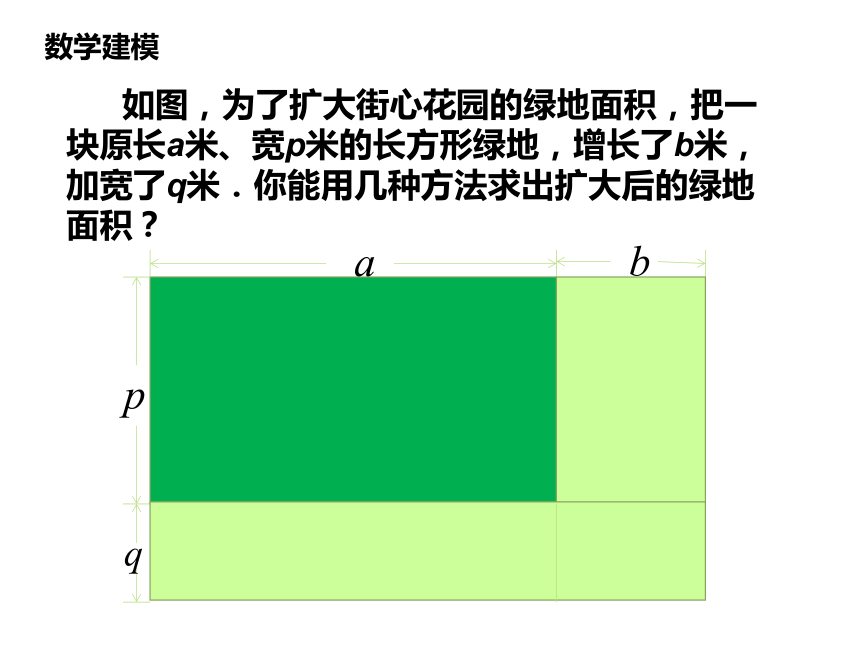
为了扩大街心花园的绿地面积,把一块原长a米、宽p米的长方形绿地,增长了b米,加宽了q米.你能用几种方法求出扩大后的绿地面积?
创设情境
a
p
b
q
如图,为了扩大街心花园的绿地面积,把一块原长a米、宽p米的长方形绿地,增长了b米,加宽了q米.你能用几种方法求出扩大后的绿地面积?
数学建模
aq
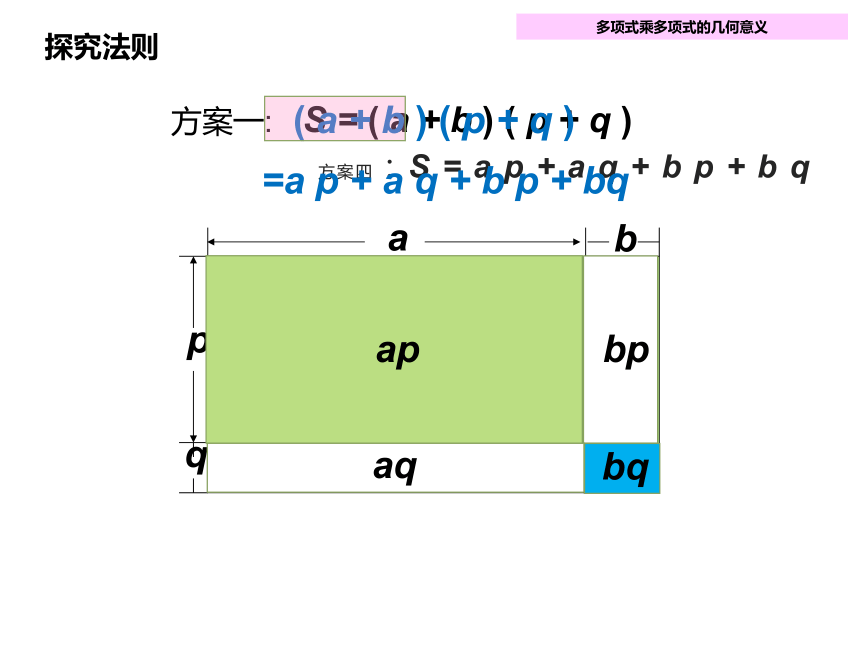
方案四:S = a p + a q + b p + bq
方案二:S = a ( p + q ) + b ( p + q )
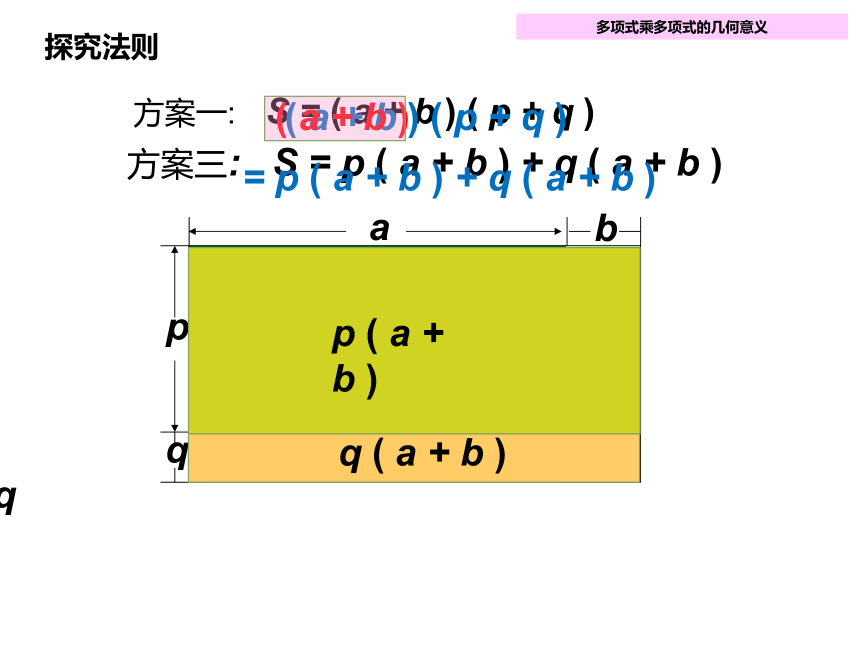
方案三: S = p ( a + b ) + q ( a + b )
方案一: S = ( a + b ) ( p + q )
p
q
a
b
探究法则
多项式乘多项式的几何意义
a
b
p
q
方案一: S = ( a + b ) ( p + q )
aq
探究法则
多项式乘多项式的几何意义
a
b
p
q
方案二:S = a ( p + q ) + b ( p + q )
a ( p + q )
b ( p + q )
aq
探究法则
多项式乘多项式的几何意义
方案一: S = ( a + b ) ( p + q )
( a + b ) ( p + q )
= a ( p + q ) + b ( p + q )
推 导
计算(a+b)(p+q),可以先把 p+q 看成一个整体,运用单项式与多项式相乘的法则,得
=a(p+q)
=ap + aq + bp + bq.
(a+b)(p+q)
b(p+q)
转化
+
多项式乘多项式的代数意义
探究法则
a
b
p
q
方案三: S = p ( a + b ) + q ( a + b )
p ( a + b )
q ( a + b )
aq
探究法则
多项式乘多项式的几何意义
方案一: S = ( a + b ) ( p + q )
( a + b ) ( p + q )
= p ( a + b ) + q ( a + b )
( a + b )
a
b
p
q
方案四:S = a p + a q + b p + b q
ap
aq
bp
探究法则
多项式乘多项式的几何意义
方案一: S = ( a + b ) ( p + q )
( a + b ) ( p + q )
=a p + a q + b p + bq
bq
( a + b ) ( p + q )
( a + b ) ( p + q )的也可以看作由 a+b 的每一项乘 p+q 的每一项,再把所得的积相加而得到的,即
推 导
=ap
bp
aq
+ + +
bq
多项式乘多项式的代数意义
探究法则
x
q
x
p
x2
px
qx
pq
( x + p )( x + q )= 2 + ( )x +
x
p+q
pq
和
积
平方
探究发现
归 纳
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(p+q) = ap+aq+bp+bq .
多项式乘多项式的计算法则
探究法则
例1 计算:
(1)(3x+1)(x - 2); (2)(x-8y)(x - y)
(3)(x+y)(x2-x y + y2)
解: (1)原式 = 3x · x
= 3 x2 – 6 x + x – 2
=3x2 – 5x – 2
带着前边的符号乘
- 2
+1
– 3x ·2
+ 1·x
– 1×2
注意符号
跟着老师学方法
应用举例
例1 计算:
(1) ( 3x + 1 )( x – 2 ) ; (2) ( x – 8 y )( x – y ) ;
(3) (x + y)(x2 – x y + y2 ).
(2)原式 = x · x – x · y – 8y · x + 8y ·y
= x2 - x y – 8xy + 8y2
= x2 - 9xy + 8y2
(3)原式 = x · x2–x ·x y +x ·y2+y ·x2-y ·xy+y ·y2
= x 3-x2 y+xy2 +x2 y–xy2+ y3
= x 3+ y3
不重不漏
注意符号
实践得真知
应用举例
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
答案: (1) 2x2+7x+3; (2) m2+5mn+6n2;
(3) a2-2a+1; (4) a2-9b2
(5) x2+5x+6; (6) x2-3x-4;
(7) y2+2y-8; (8) y2-8y+15.
巩固练习
实践得真知
( x + p )( x + q )= ( )2 + ( )x + ( )
(5) ( x + 2) ( x + 3)
(6) ( x – 4) ( x + 1)
(7) ( y + 4) ( y – 2)
(8) ( y – 5) ( y – 3)
观察上述式子,你可以 得出一个什么规律吗?
= x2 + 5x + 6 ;
= x2 – 3x – 4 ;
= y2 + 2y – 8 ;
= y2 – 8y + 15 .
由上面的计算结果找出的规律,观察下图填空:
x
q
x
p
x2
px
qx
pq
和
积
x
p+q
pq
x,y的系数是 1
x 的系数是 1
和
积
探究发现
口答:
① ( x + 2 ) ( x + 3 )
② ( x – 1 ) ( x +2 )
③ ( x + 2 ) ( x – 2 )
④ ( x – 5 ) ( x – 6 )
⑤ ( x + 5 ) ( x + 5 )
⑥ ( x – 5 ) ( x – 5 )
= x2 + 5x + 6
= x2 + x – 2
= x2 – 4
= x2 – 11x + 30
= x2 + 10x + 25
= x2 – 10x + 25
x2 +和x+积
巩固练习
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
知识总结
(a+b)(m+n) = am+an+bm+bn .
( x + p )( x + q )= 2 + ( )x +
x
p+q
pq
和
积
不重
不漏
x 的系数是1
平方
课堂小结
注意
符号
数学建模
推
理
验
证
探究发现
问题解决
方法归纳
课堂小结
课堂小结
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(p+q)=ap+aq+bp+bq
随堂演练
计算:
(1)(x-3y)(x+7y)
(2)(2x+5y)(3x-2y)
(3)(1-x)(0.6-x)
(4)(x-y)2
x2+4xy-21y2
6x2+11xy-10y2
x2-1.6x+0.6
x2-2xy+y2
计算:
(1)(x-3y)(x+7y) (2)(2x+5y)(3x-2y)
解:
(1)原式=x2+7xy-3xy-21y2
(2)原式=6x2-4xy+15xy-10y2
强化练习
=x2+4xy-21y2
=6x2+11xy-10y2
2.确定(x+2)(x+m)=x2+nx+16中m和p的值.
拓展延伸
解:(x+2)(x+m)=x2+mx+2x+2m
=x2+(m+2)x+2m
又∵(x+2)(x+m)=x2+nx+16
∴x2+(m+2)x+2m=x2+nx+16
∴ m=8,
n=m+2=10
—多项式乘多项式
人教版 八年级 上册
m
n
a
b
bn
bm
am
an
为了扩大街心花园的绿地面积,把一块原长a米、宽p米的长方形绿地,增长了b米,加宽了q米.你能用几种方法求出扩大后的绿地面积?
创设情境
a
p
b
q
如图,为了扩大街心花园的绿地面积,把一块原长a米、宽p米的长方形绿地,增长了b米,加宽了q米.你能用几种方法求出扩大后的绿地面积?
数学建模
aq
方案四:S = a p + a q + b p + bq
方案二:S = a ( p + q ) + b ( p + q )
方案三: S = p ( a + b ) + q ( a + b )
方案一: S = ( a + b ) ( p + q )
p
q
a
b
探究法则
多项式乘多项式的几何意义
a
b
p
q
方案一: S = ( a + b ) ( p + q )
aq
探究法则
多项式乘多项式的几何意义
a
b
p
q
方案二:S = a ( p + q ) + b ( p + q )
a ( p + q )
b ( p + q )
aq
探究法则
多项式乘多项式的几何意义
方案一: S = ( a + b ) ( p + q )
( a + b ) ( p + q )
= a ( p + q ) + b ( p + q )
推 导
计算(a+b)(p+q),可以先把 p+q 看成一个整体,运用单项式与多项式相乘的法则,得
=a(p+q)
=ap + aq + bp + bq.
(a+b)(p+q)
b(p+q)
转化
+
多项式乘多项式的代数意义
探究法则
a
b
p
q
方案三: S = p ( a + b ) + q ( a + b )
p ( a + b )
q ( a + b )
aq
探究法则
多项式乘多项式的几何意义
方案一: S = ( a + b ) ( p + q )
( a + b ) ( p + q )
= p ( a + b ) + q ( a + b )
( a + b )
a
b
p
q
方案四:S = a p + a q + b p + b q
ap
aq
bp
探究法则
多项式乘多项式的几何意义
方案一: S = ( a + b ) ( p + q )
( a + b ) ( p + q )
=a p + a q + b p + bq
bq
( a + b ) ( p + q )
( a + b ) ( p + q )的也可以看作由 a+b 的每一项乘 p+q 的每一项,再把所得的积相加而得到的,即
推 导
=ap
bp
aq
+ + +
bq
多项式乘多项式的代数意义
探究法则
x
q
x
p
x2
px
qx
pq
( x + p )( x + q )= 2 + ( )x +
x
p+q
pq
和
积
平方
探究发现
归 纳
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(p+q) = ap+aq+bp+bq .
多项式乘多项式的计算法则
探究法则
例1 计算:
(1)(3x+1)(x - 2); (2)(x-8y)(x - y)
(3)(x+y)(x2-x y + y2)
解: (1)原式 = 3x · x
= 3 x2 – 6 x + x – 2
=3x2 – 5x – 2
带着前边的符号乘
- 2
+1
– 3x ·2
+ 1·x
– 1×2
注意符号
跟着老师学方法
应用举例
例1 计算:
(1) ( 3x + 1 )( x – 2 ) ; (2) ( x – 8 y )( x – y ) ;
(3) (x + y)(x2 – x y + y2 ).
(2)原式 = x · x – x · y – 8y · x + 8y ·y
= x2 - x y – 8xy + 8y2
= x2 - 9xy + 8y2
(3)原式 = x · x2–x ·x y +x ·y2+y ·x2-y ·xy+y ·y2
= x 3-x2 y+xy2 +x2 y–xy2+ y3
= x 3+ y3
不重不漏
注意符号
实践得真知
应用举例
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
答案: (1) 2x2+7x+3; (2) m2+5mn+6n2;
(3) a2-2a+1; (4) a2-9b2
(5) x2+5x+6; (6) x2-3x-4;
(7) y2+2y-8; (8) y2-8y+15.
巩固练习
实践得真知
( x + p )( x + q )= ( )2 + ( )x + ( )
(5) ( x + 2) ( x + 3)
(6) ( x – 4) ( x + 1)
(7) ( y + 4) ( y – 2)
(8) ( y – 5) ( y – 3)
观察上述式子,你可以 得出一个什么规律吗?
= x2 + 5x + 6 ;
= x2 – 3x – 4 ;
= y2 + 2y – 8 ;
= y2 – 8y + 15 .
由上面的计算结果找出的规律,观察下图填空:
x
q
x
p
x2
px
qx
pq
和
积
x
p+q
pq
x,y的系数是 1
x 的系数是 1
和
积
探究发现
口答:
① ( x + 2 ) ( x + 3 )
② ( x – 1 ) ( x +2 )
③ ( x + 2 ) ( x – 2 )
④ ( x – 5 ) ( x – 6 )
⑤ ( x + 5 ) ( x + 5 )
⑥ ( x – 5 ) ( x – 5 )
= x2 + 5x + 6
= x2 + x – 2
= x2 – 4
= x2 – 11x + 30
= x2 + 10x + 25
= x2 – 10x + 25
x2 +和x+积
巩固练习
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
知识总结
(a+b)(m+n) = am+an+bm+bn .
( x + p )( x + q )= 2 + ( )x +
x
p+q
pq
和
积
不重
不漏
x 的系数是1
平方
课堂小结
注意
符号
数学建模
推
理
验
证
探究发现
问题解决
方法归纳
课堂小结
课堂小结
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(p+q)=ap+aq+bp+bq
随堂演练
计算:
(1)(x-3y)(x+7y)
(2)(2x+5y)(3x-2y)
(3)(1-x)(0.6-x)
(4)(x-y)2
x2+4xy-21y2
6x2+11xy-10y2
x2-1.6x+0.6
x2-2xy+y2
计算:
(1)(x-3y)(x+7y) (2)(2x+5y)(3x-2y)
解:
(1)原式=x2+7xy-3xy-21y2
(2)原式=6x2-4xy+15xy-10y2
强化练习
=x2+4xy-21y2
=6x2+11xy-10y2
2.确定(x+2)(x+m)=x2+nx+16中m和p的值.
拓展延伸
解:(x+2)(x+m)=x2+mx+2x+2m
=x2+(m+2)x+2m
又∵(x+2)(x+m)=x2+nx+16
∴x2+(m+2)x+2m=x2+nx+16
∴ m=8,
n=m+2=10
