人教版八年级数学上册教学课件-14.2.1 平方差公式3(共17张ppt)
文档属性
| 名称 | 人教版八年级数学上册教学课件-14.2.1 平方差公式3(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 548.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 16:44:48 | ||
图片预览





文档简介
14.2 平方差公式
初中人教版课程标准教科书
八年级上册
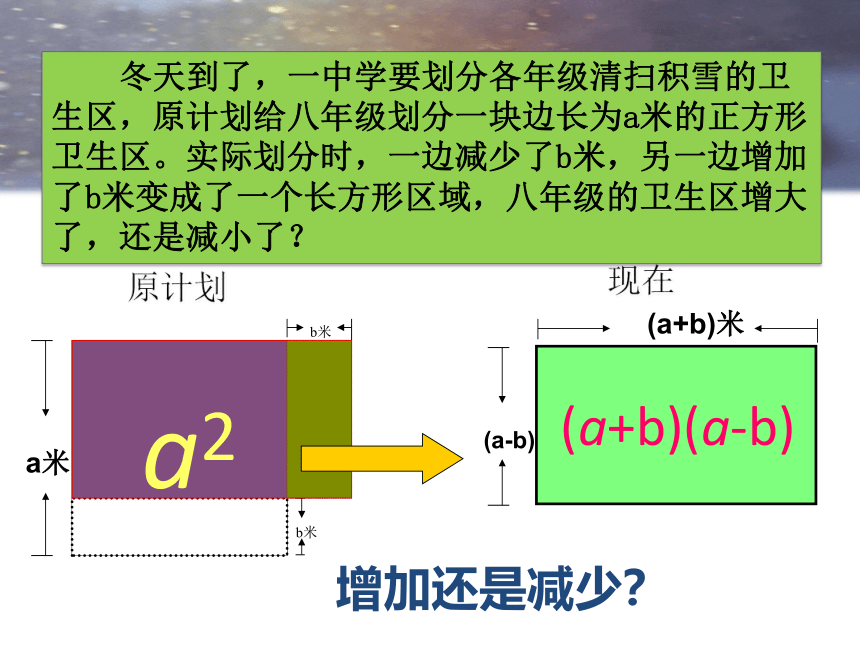
冬天到了,一中学要划分各年级清扫积雪的卫生区,原计划给八年级划分一块边长为a米的正方形卫生区。实际划分时,一边减少了b米,另一边增加了b米变成了一个长方形区域,八年级的卫生区增大了,还是减小了?
b米
b米
a米
(a-b)
(a+b)米
增加还是减少?
原计划
现在
a2
(a+b)(a-b)
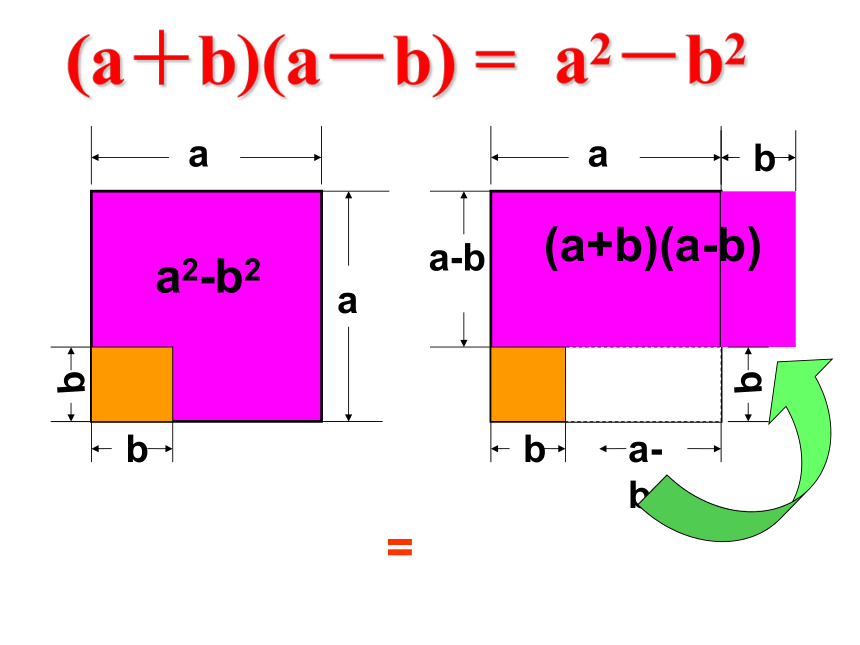
(a+b)(a-b) =
a2-b2
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
(a+b)(a-b) =
a2-b2
计算下列多项式的积.
(1)(x+1)(x-1)
(2)(m+2)(m-2)
(3) (2x+1)(2 x?1)
= x2-1
= m2-4
= 4x2 - 1
12
12
22
(2x)2
( )( ) =
两个数的和与这两个数的差的积,等于这两个数的平方差.
1.左边两个多项式相乘,这两个二项式中
有一项完全相同,另一项互为相反数.
2.右边是相同项的平方减去相反项的平方的差.
3.公式中的 a和b 可以是数,也可以是代数式.
a
a
-b2
-b
+b
完全相同
互为相反数
相同项的平方
相反项的平方
平方差公式
a2
(条件)
(结果)
(1) (? a+b)(?a?b)
(2) (a?b) (b?a)
(3) (a+b) (b-a)
(4) (?x+y)(y?x)
(不能)
(不能)
(能)
(能)
练习:
判断下列式子能否用平方差公式计算.
例1 利用平方差公式计算:
(1)(3x+2) (3x ?2)
(2)(?x+2y) (?x?2y)
(3)(?3x?5)(3x?5)
例2 计算:
1. 102×98
2. 1002× 1998
练习一
( )
(x4+y4 )
(x4+y4 )
(x4+y4)
如果(x+y-3)2+(x-y+5)2=0,求x2-y2
练习二
1、 ( ) ( ) =4x2-9y2
2、(5+a)( ) =25-a?
a? - b? =(a+b)(a-b)
练习三
1.平方差公式:(a+b)(a-b)=a2-b2
两数和与这两数差的积等于这两数的平方差.
2.学会运用平方差公式进行计算.
小结:
3.数学思想:数形结合,从特殊到一般
布置作业:
1. 必做题: 习题 14.2 第 1 题
2. 选做题:
(1) 计算 (x+y)(x+y)
(2) 在式子 (-3a+ 2b )( ) 的括号内填入怎样的式子才能用平方差公式计算?
2. 计算: 1234567 × 1234569 - 1234568 ?
随堂练习
?
m
3
c
?
2
?
(1) (3x+2)(3x-2)
变式一 ( -3x+2)(-3x-2)
变式二 ( -3x-2)(3x-2)
变式三 (-3x+2)(3x+2)
=(-3x)2-22
变一变,你还能做吗?
课堂检测
?
?
3. 运用平方差公式计算:
(1)(5+2y)(5-2y); (2)2001×1999
?
谢谢大家!
初中人教版课程标准教科书
八年级上册
冬天到了,一中学要划分各年级清扫积雪的卫生区,原计划给八年级划分一块边长为a米的正方形卫生区。实际划分时,一边减少了b米,另一边增加了b米变成了一个长方形区域,八年级的卫生区增大了,还是减小了?
b米
b米
a米
(a-b)
(a+b)米
增加还是减少?
原计划
现在
a2
(a+b)(a-b)
(a+b)(a-b) =
a2-b2
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
(a+b)(a-b) =
a2-b2
计算下列多项式的积.
(1)(x+1)(x-1)
(2)(m+2)(m-2)
(3) (2x+1)(2 x?1)
= x2-1
= m2-4
= 4x2 - 1
12
12
22
(2x)2
( )( ) =
两个数的和与这两个数的差的积,等于这两个数的平方差.
1.左边两个多项式相乘,这两个二项式中
有一项完全相同,另一项互为相反数.
2.右边是相同项的平方减去相反项的平方的差.
3.公式中的 a和b 可以是数,也可以是代数式.
a
a
-b2
-b
+b
完全相同
互为相反数
相同项的平方
相反项的平方
平方差公式
a2
(条件)
(结果)
(1) (? a+b)(?a?b)
(2) (a?b) (b?a)
(3) (a+b) (b-a)
(4) (?x+y)(y?x)
(不能)
(不能)
(能)
(能)
练习:
判断下列式子能否用平方差公式计算.
例1 利用平方差公式计算:
(1)(3x+2) (3x ?2)
(2)(?x+2y) (?x?2y)
(3)(?3x?5)(3x?5)
例2 计算:
1. 102×98
2. 1002× 1998
练习一
( )
(x4+y4 )
(x4+y4 )
(x4+y4)
如果(x+y-3)2+(x-y+5)2=0,求x2-y2
练习二
1、 ( ) ( ) =4x2-9y2
2、(5+a)( ) =25-a?
a? - b? =(a+b)(a-b)
练习三
1.平方差公式:(a+b)(a-b)=a2-b2
两数和与这两数差的积等于这两数的平方差.
2.学会运用平方差公式进行计算.
小结:
3.数学思想:数形结合,从特殊到一般
布置作业:
1. 必做题: 习题 14.2 第 1 题
2. 选做题:
(1) 计算 (x+y)(x+y)
(2) 在式子 (-3a+ 2b )( ) 的括号内填入怎样的式子才能用平方差公式计算?
2. 计算: 1234567 × 1234569 - 1234568 ?
随堂练习
?
m
3
c
?
2
?
(1) (3x+2)(3x-2)
变式一 ( -3x+2)(-3x-2)
变式二 ( -3x-2)(3x-2)
变式三 (-3x+2)(3x+2)
=(-3x)2-22
变一变,你还能做吗?
课堂检测
?
?
3. 运用平方差公式计算:
(1)(5+2y)(5-2y); (2)2001×1999
?
谢谢大家!
