人教版九年级数学上册 课件 第二十四章 圆 24.2.2直线与圆的位置关系(共22张ppt)
文档属性
| 名称 | 人教版九年级数学上册 课件 第二十四章 圆 24.2.2直线与圆的位置关系(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 11:55:13 | ||
图片预览







文档简介
第二十四章 圆
24.2.2直线与圆的位置关系
第一课时
【学习目标】
1.理解掌握同一平面内的直线与圆的三种位置关系.
2.理解记忆割线、切线、切点等概念.
3.能根据圆心到直线的距离d与半径r的大小关系,准确判断出直线与圆的位置关系。
【课前预习】
1.在 以点C为圆心,2cm长为半径的圆与AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.下列说法正确的个数是( )
①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.
A.1 B.2 C.3 D.4
3.在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相离
C.与x轴相离,与y轴相切 D.与x轴相离,与y轴相离
4.已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A.相切 B.相交 C.相离 D.不能确定
5.已知⊙O的直径为4cm,圆心到直线l1, l2, l3, l4的距离分别为2cm, ,则与⊙O相切的直线有( )
A.1条 B.2条 C.3条 D.4条
【课前预习】答案
1.C
2.A
3.B
4.D
5.B
1.情境引入
1.情境引入
1.情境引入
2.直线和圆的位置关系
l
O
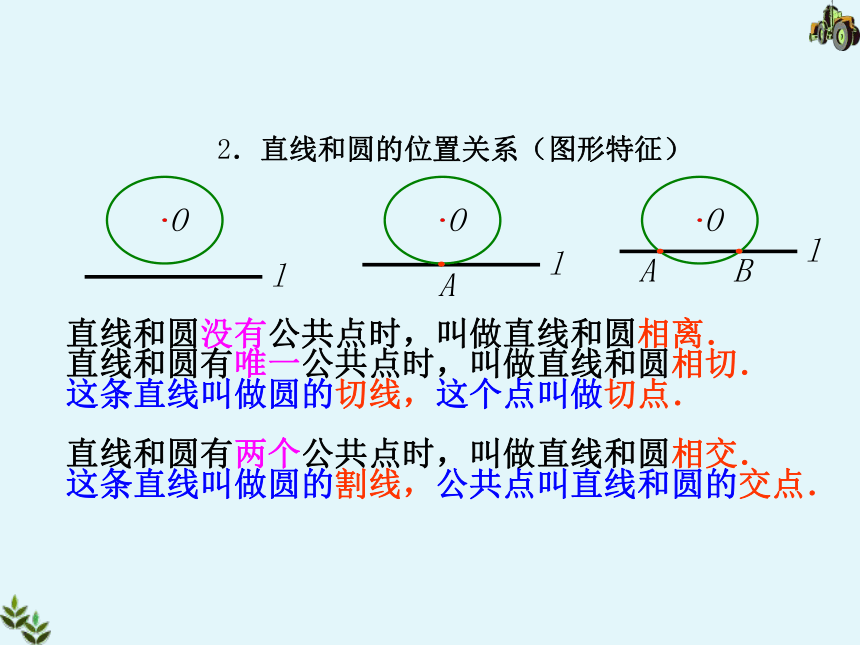
这条直线叫做圆的割线,公共点叫直线和圆的交点.
直线和圆没有公共点时,叫做直线和圆相离.
直线和圆有唯一公共点时,叫做直线和圆相切.
直线和圆有两个公共点时,叫做直线和圆相交.
这条直线叫做圆的切线,这个点叫做切点.
2.直线和圆的位置关系(图形特征)
l
O
l
O
A
l
O
A
B
1.能否根据基本概念判断直线和圆的位置关系?
直线 l 和⊙O 没有公共点 直线 l 和⊙O 相离.
直线 l 和⊙O 只有一个公共点 直线 l 和⊙O 相切.
直线 l 和⊙O 有两个公共点 直线 l 和⊙O 相交.
2.是否还有其他的方法判断直线和圆的位置关系?
用公共点的个数来判断直线和圆的位置关系.
2.直线和圆的位置关系(图形特征)
1.直线和圆相离 d>r;
2.直线和圆相切 d=r;
3.直线和圆相交 d<r.
2.直线和圆的位置关系(数量特征)
相离
相切
l
O
相交
l
O
A
l
O
A
B
d
r
d
r
d
r
当直线和圆相离、相切、相交时,d 与 r 有何关系?
直线和圆的位置关系的识别与特征:
小结:利用圆心到直线的距离与半径的大小关系来识别直线和圆的位置关系.
直线和圆的位置关系
相 交
相 切
相 离
图 形
公共点个数
公共点名称
-
直线名称
-
距离 d 与半径 r 的关系
l
O
d
r
l
O
A
B
d
r
l
O
A
d
r
2 个
交点
割线
1 个
切点
切线
d<r
d=r
d>r
没有
练习1 圆的直径是 13 cm,如果直线和圆心的距离
分别是 ① 4.5 cm;② 6.5 cm;③ 8 cm,那么直线和圆分
别是什么位置关系?有几个公共点?
4.练习
练习2 已知⊙A 的直径为 6,点 A 的坐标为(-3,
-4),则⊙A 与 x 轴的位置关系是_____,⊙A 与 y 轴的位置关系是______.
相离
相切
y
x
A
-3
-4
O
例 Rt△ABC,∠C=90°,AC=3 cm,BC=4 cm,
以 C 为圆心,r 为半径的圆与 AB 有怎样的位置关系?
为什么?
(1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm.
分析:
根据直线和圆的位置关系
的数量特征,应该用圆心到直
线的距离 d 与半径 r 的大小进
行比较;
关键是确定圆心 C 到直线
AB 的距离 d,这个距离是多少
呢?怎么求这个距离?
C
B
A
d
d=2.4 cm
D
即圆心 C 到 AB 的距离 d = 2.4cm.
(1)当 r = 2 cm 时,∵ d >r,∴ ⊙C 与 AB 相离.
(2)当 r = 2.4 cm 时,∵ d = r,∴ ⊙C 与 AB 相切.
(3)当 r = 3 cm 时,∵ d <r,∴ ⊙C 与 AB 相交.
解:过 C 作 CD⊥AB,垂足为 D.
根据三角形面积公式有
CD · AB=AC · BC
在 Rt△ABC 中, AB= (cm)
∴ CD= (cm).
练习3 已知⊙O 到直线 l 的距离为 d,⊙O 的半径为 r,若 d、r 是方程 x 2 - 7x + 12 = 0 的两个根,则直线 l
和⊙O 的位置关系是______________.
相交或相离
1.直线和圆的位置关系有三种:相离、相切和相交.
5.课堂小结
2.识别直线和圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线 l 和⊙O 没有公共点 直线 l 和⊙O 相离;
直线 l 和⊙O 只有一个公共点 直线 l 和⊙O 相切;
直线 l 和⊙O 有两个公共点 直线 l 和⊙O 相交.
(2)另一种是根据圆心到直线的距离 d 与圆半径
r 的大小关系来进行识别:
d >r 直线 l 和⊙O 相离;
d =r 直线 l 和⊙O 相切;
d <r 直线 l 和⊙O 相交.
3.谈谈这节课你学习的收获.
【课后练习】
1.已知⊙O的半径为4,直线l上有一点与⊙O的圆心的距离为4,则直线l与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相切、相交均有可能
2.△ABC中,∠C=90°,AB=13,AC=12,以B为圆心,5为半径的圆与直线AC的位置关系是( )
A.相切 B.相交 C.相离 D.不能确定
3.菱形的对角线相交于O,以O为圆心,以点O到菱形一边的距离为半径的⊙O与菱形其它三边的位置关系是( )
A.相交 B.相离 C.相切 D.无法确定
4.已知某直线到圆心的距离为5cm,圆的周长为 ,请问这条直线与这个圆的公共点的个数为( )
A.0 B.1 C.2 D.无法确定
5.
A.一定相交 B.一定相切C.一定相离D.可能相交,也可能相切或相离
6.直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则r的取值是( )
A.r>5 B.r=5 C.r<5 D.r≤5
7.已知直线l经过⊙O上的A,B两点,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.无法确定
8.在边长为1的等边三角形ABC中,以A为圆心, 以 为半径的圆与BC边的位置关系是( ).
A.相交 B.相离 C.相切 D.相交或相离
9.△ABC中,以AB边上的高为直径作一个圆,则与这个圆相切的直线是( ).
A.AB B.AC C.BC D.不确定
10.如果直线l与⊙O有公共点,那么直线l与⊙O的位置关系是 ( )
A.相交 B.相切 C.相离 D.相切或相交
【课后练习】答案
1.D 2.A 3.C 4.B 5.D 6.A 7.B 8.C 9.A 10.D
11.相离或相交
12.相交
13.相切
14.
15.2 1 0条
24.2.2直线与圆的位置关系
第一课时
【学习目标】
1.理解掌握同一平面内的直线与圆的三种位置关系.
2.理解记忆割线、切线、切点等概念.
3.能根据圆心到直线的距离d与半径r的大小关系,准确判断出直线与圆的位置关系。
【课前预习】
1.在 以点C为圆心,2cm长为半径的圆与AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.下列说法正确的个数是( )
①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.
A.1 B.2 C.3 D.4
3.在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相离
C.与x轴相离,与y轴相切 D.与x轴相离,与y轴相离
4.已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A.相切 B.相交 C.相离 D.不能确定
5.已知⊙O的直径为4cm,圆心到直线l1, l2, l3, l4的距离分别为2cm, ,则与⊙O相切的直线有( )
A.1条 B.2条 C.3条 D.4条
【课前预习】答案
1.C
2.A
3.B
4.D
5.B
1.情境引入
1.情境引入
1.情境引入
2.直线和圆的位置关系
l
O
这条直线叫做圆的割线,公共点叫直线和圆的交点.
直线和圆没有公共点时,叫做直线和圆相离.
直线和圆有唯一公共点时,叫做直线和圆相切.
直线和圆有两个公共点时,叫做直线和圆相交.
这条直线叫做圆的切线,这个点叫做切点.
2.直线和圆的位置关系(图形特征)
l
O
l
O
A
l
O
A
B
1.能否根据基本概念判断直线和圆的位置关系?
直线 l 和⊙O 没有公共点 直线 l 和⊙O 相离.
直线 l 和⊙O 只有一个公共点 直线 l 和⊙O 相切.
直线 l 和⊙O 有两个公共点 直线 l 和⊙O 相交.
2.是否还有其他的方法判断直线和圆的位置关系?
用公共点的个数来判断直线和圆的位置关系.
2.直线和圆的位置关系(图形特征)
1.直线和圆相离 d>r;
2.直线和圆相切 d=r;
3.直线和圆相交 d<r.
2.直线和圆的位置关系(数量特征)
相离
相切
l
O
相交
l
O
A
l
O
A
B
d
r
d
r
d
r
当直线和圆相离、相切、相交时,d 与 r 有何关系?
直线和圆的位置关系的识别与特征:
小结:利用圆心到直线的距离与半径的大小关系来识别直线和圆的位置关系.
直线和圆的位置关系
相 交
相 切
相 离
图 形
公共点个数
公共点名称
-
直线名称
-
距离 d 与半径 r 的关系
l
O
d
r
l
O
A
B
d
r
l
O
A
d
r
2 个
交点
割线
1 个
切点
切线
d<r
d=r
d>r
没有
练习1 圆的直径是 13 cm,如果直线和圆心的距离
分别是 ① 4.5 cm;② 6.5 cm;③ 8 cm,那么直线和圆分
别是什么位置关系?有几个公共点?
4.练习
练习2 已知⊙A 的直径为 6,点 A 的坐标为(-3,
-4),则⊙A 与 x 轴的位置关系是_____,⊙A 与 y 轴的位置关系是______.
相离
相切
y
x
A
-3
-4
O
例 Rt△ABC,∠C=90°,AC=3 cm,BC=4 cm,
以 C 为圆心,r 为半径的圆与 AB 有怎样的位置关系?
为什么?
(1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm.
分析:
根据直线和圆的位置关系
的数量特征,应该用圆心到直
线的距离 d 与半径 r 的大小进
行比较;
关键是确定圆心 C 到直线
AB 的距离 d,这个距离是多少
呢?怎么求这个距离?
C
B
A
d
d=2.4 cm
D
即圆心 C 到 AB 的距离 d = 2.4cm.
(1)当 r = 2 cm 时,∵ d >r,∴ ⊙C 与 AB 相离.
(2)当 r = 2.4 cm 时,∵ d = r,∴ ⊙C 与 AB 相切.
(3)当 r = 3 cm 时,∵ d <r,∴ ⊙C 与 AB 相交.
解:过 C 作 CD⊥AB,垂足为 D.
根据三角形面积公式有
CD · AB=AC · BC
在 Rt△ABC 中, AB= (cm)
∴ CD= (cm).
练习3 已知⊙O 到直线 l 的距离为 d,⊙O 的半径为 r,若 d、r 是方程 x 2 - 7x + 12 = 0 的两个根,则直线 l
和⊙O 的位置关系是______________.
相交或相离
1.直线和圆的位置关系有三种:相离、相切和相交.
5.课堂小结
2.识别直线和圆的位置关系的方法:
(1)一种是根据定义进行识别:
直线 l 和⊙O 没有公共点 直线 l 和⊙O 相离;
直线 l 和⊙O 只有一个公共点 直线 l 和⊙O 相切;
直线 l 和⊙O 有两个公共点 直线 l 和⊙O 相交.
(2)另一种是根据圆心到直线的距离 d 与圆半径
r 的大小关系来进行识别:
d >r 直线 l 和⊙O 相离;
d =r 直线 l 和⊙O 相切;
d <r 直线 l 和⊙O 相交.
3.谈谈这节课你学习的收获.
【课后练习】
1.已知⊙O的半径为4,直线l上有一点与⊙O的圆心的距离为4,则直线l与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相切、相交均有可能
2.△ABC中,∠C=90°,AB=13,AC=12,以B为圆心,5为半径的圆与直线AC的位置关系是( )
A.相切 B.相交 C.相离 D.不能确定
3.菱形的对角线相交于O,以O为圆心,以点O到菱形一边的距离为半径的⊙O与菱形其它三边的位置关系是( )
A.相交 B.相离 C.相切 D.无法确定
4.已知某直线到圆心的距离为5cm,圆的周长为 ,请问这条直线与这个圆的公共点的个数为( )
A.0 B.1 C.2 D.无法确定
5.
A.一定相交 B.一定相切C.一定相离D.可能相交,也可能相切或相离
6.直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则r的取值是( )
A.r>5 B.r=5 C.r<5 D.r≤5
7.已知直线l经过⊙O上的A,B两点,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.无法确定
8.在边长为1的等边三角形ABC中,以A为圆心, 以 为半径的圆与BC边的位置关系是( ).
A.相交 B.相离 C.相切 D.相交或相离
9.△ABC中,以AB边上的高为直径作一个圆,则与这个圆相切的直线是( ).
A.AB B.AC C.BC D.不确定
10.如果直线l与⊙O有公共点,那么直线l与⊙O的位置关系是 ( )
A.相交 B.相切 C.相离 D.相切或相交
【课后练习】答案
1.D 2.A 3.C 4.B 5.D 6.A 7.B 8.C 9.A 10.D
11.相离或相交
12.相交
13.相切
14.
15.2 1 0条
同课章节目录
