人教版七年级数学上册 第四章 几何图形初步 4.2 直线、射线、线段 课件(共37张ppt)
文档属性
| 名称 | 人教版七年级数学上册 第四章 几何图形初步 4.2 直线、射线、线段 课件(共37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 16:54:35 | ||
图片预览










文档简介
第四章 几何图形初步
4.2 直线、射线、线段
【学习目标】
1、了解射线的定义、射线的表示方法及特征.
2、会用尺规画一条线段等于已知线段;会利用直尺和圆规比较两条线段的长短;
3、明白线段中点概念,并会运用;明白并会应用“两点之间线段最短”性质。
【课前预习】
1.在直线 l 上取 A、B、C 三点,使得 AB=5 cm,BC=3 cm,如果点 O 是线段 AC 的中点,那么线段 OB 的长度是( )
A.4 cm B.1 cm C.1.5 cm D.1 cm 或 4 cm
2.下列语句正确的有( )
(1)线段AB就是A、B两点间的距离;(2)画射线AB=10cm;(3)A,B两点之间的所有连线中,最短的是线段AB;(4)在直线上取A,B,C三点,若AB=5cm,BC=2cm,则AC=7cm.
A.1个 B.2个 C.3个 D.4个
3.下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是( )
A.用两个钉子就可以把木条固定在墙上 B.利用圆规可以比较两条线段的大小关系 C.把弯曲的公路改直,就能缩短路程 D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
4.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ).
A.1 B.2 C.1或2或3 D.0或1或2或3
5.在平面上有任意四个点,那么这四个点可以确定的直线有( )
A.1条 B.4条 C.6条 D.1条或4条或6条
【课前预习】答案
1.D
2.A
3.C
4.C
5.D
(1)经过一点O可以画几条直线?
(2)经过两点A、B可以画直线吗?可
以画几条?
画一画
·o
·A
·B
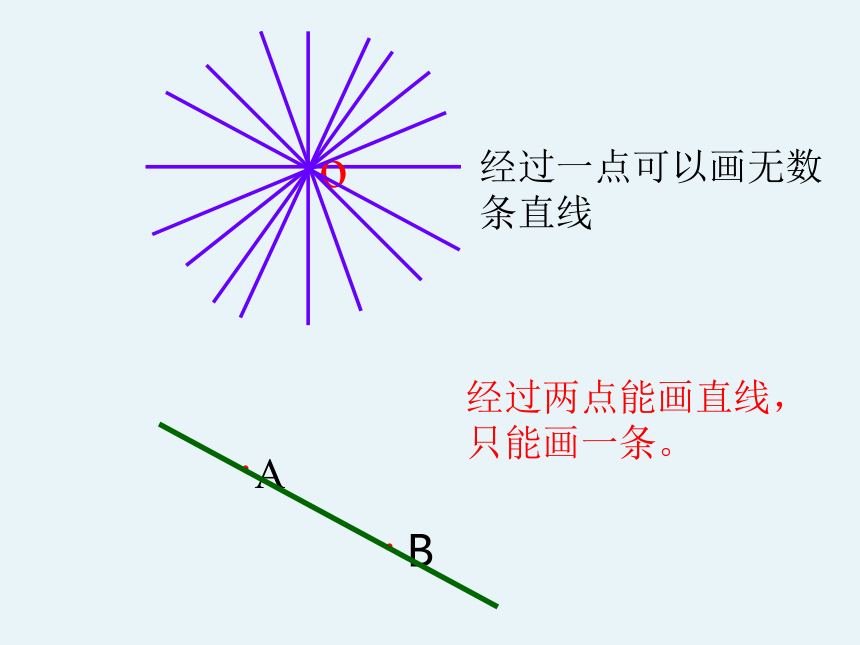
经过一点可以画无数条直线
经过两点能画直线,只能画一条。
经过两点有一条直线,并且只有一条直线
简述为:两点确定一条直线
直线的性质
生活中我们常常用到两点确定一条
直线,你能举几个例子吗?
植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
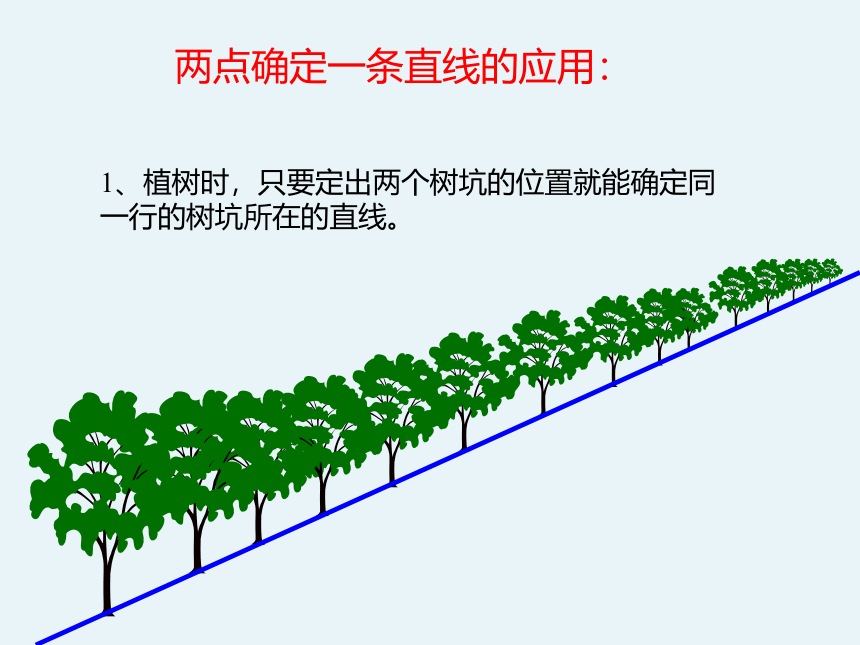
两点确定一条直线的应用:
两点确定一条直线的应用:
1、植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
建筑工人在砌墙时经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线, 根据 道理.
两点确定一条直线的
怎样用数学符号表示直线?
A
B
(2)我们还可以用一个小写字母来表示一条直线。
如下列直线记作直线l。
A
B
直线的表示方法
l
(1)我们用直线上的两个点来表示这条直线。
如下列直线记作直线AB或直线BA。
点和直线的关系
直线和直线的关系
ι
O
A
B
点O在直线ι上(直线ι经过点O);
点A、B 在直线ι外(直线 ι不经过点A 、B)。
a
b
O
直线a和b相交于点O
当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
O
A
B
表示:线段 AB(或线段BA)
a
表示:线段 a
A
表示:射线OA
表示:射线b
b
线段、射线的表示方法
线段: ①用两个端点的字母来表示,无先后顺序。可度量
②用一个小写字母表示。
射线: ① 用端点及射线上一点来表示,不可度量
注意端点的字母写在前面。
②用一个小写字母表示。
直线: ①用直线上两个点来表示,无先后顺序,不可度量。
②用一个小写字母来表示。
归纳总结
你发现直线、射线、线段有什么联系吗?又有什么区别呢?
发现
图形
表示方法
端点个数
延伸方向
线段
射线
直线
直线、射线、线段的联系与区别?
A
B
a
A
B
a
线段AB或线段a
射线AB或射线a
直线AB或直线a
两个
一个
0
不向任何一方延伸
向一方无限延伸
向两方无限延伸
A
B
a
注意:
(1)表示线段、射线、直线的时候,都要在字母前注明“线段” “射线 ” “直线”。
(2)用两个大写字母表示直线或线段时,两个字母可以交换位置,表示射线的两个大写
字母不能交换位置,必须把端点字母放在前面。
指出下图中线段、射线、直线分别有多少条?
A
B
C
答:
有3条线段,是线段 AB、线段 AC、线段 BC
有6条射线。
只有一条直线,是直线 AB或直线 BC或直线AC。
你会数吗?
点与直线的位置关系
点A在直线a外
点B在直线a上
点C在直线a外
a
A
B
C
直线 a 经过点 B
直线 a 不经过点 A
直线 a 不经过点 C
如图,分别过点A、C和点B、C画直线,所画的直线有怎样的位置关系?
·B
·C
A·
当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫做它们的交点
(1)经过一点O可以画几条直线?
(2)经过两点A、B可以画直线吗?可 以画几条?
探究
画一画
·o
·A
·B
经过一点可以画无数条直线
经过两点能画直线,只能画一条。
如果将细木条抽象成直线,将钉子抽象为点,你可以得出什么结论?
过两点有且只有一条直线。
简单说成:两点确定一条直线。
猜想
基本事实
实践乐园
植树节,同学要把一排树植整齐,怎么办?
只要定出两个树坑的位置就能
确定同一行的树坑所在的直线
实践乐园
建筑工人在砌墙时会在墙的两头分别固定两枚钉子,然后在钉子之间拉一条绳子,定出一条直的参照线,这样砌出的墙就是直的;同理木工师傅经过刨平的木板上的两个点,能弹出一条笔直的墨线
按语句画图:
2、点A在直线a外;
3、经过点O的三条线段a、b、c;
4、线段AB、CD相交于点B。
1、直线EF经过点C;
活动4
1、直线EF经过点C;
E
F
C
2、点A在直线a外;
a
A
3、经过点O的三条线段a、b、c;
a
b
c
O
4、线段AB、CD相交于点B。
A
B
C
D
1 .进一步认识了线段、射线和直线的概
念,知道了它们的表示方法。
2、探索出“经过两点有且只有一条直线”的性质,并了解其在生活中的运用,体会到数学就在我们身边。
谈谈你的收获
3.利用线段、射线和直线可以创造出很多美丽的图案,用它们可以美化我们的生活。
挑战:你能用线段、射线或直线
创造出美丽的图案吗?
发挥自己的想象,课后完成自己的创作。
【课后练习】
1.如果线段AB=5cm,BC=4cm,且A、B、C在同一条直线上,那么A、C两点间的距离是( )
A.1cm B.9cm C.1cm或9cm D.12cm
2.下列说法:
①过两点有且只有一条直线;②连接两点的线段叫两点的距离;③两点之间线段最短;④如果AB=BC,则点B是AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.点 A、B、C 在同一条数轴上,其中点 A、B 表示的数分别为﹣3、1,若 BC=2,则 AC 等于( )
A.3 B.2 C.3 或 5 D.2 或 6
4.下列生活、生产现象:①用两颗钉子就可以把木条固定在墙上;②从甲地到乙地架设电线,总是沿线段架设;③把弯曲的公路改直就能缩短路程;④植树时只要确定两棵树的位置,就能确定同一行树所在的直线.其中能用“两点之间线段最短”来解释的现象是( )
A.①② B.②③ C.①④ D.③④
5.已知线段AB,C是直线AB上的一点,AB=8,BC=4,点M是线段AC的中点,则线段AM的长为( )
A.2 B.4 C.4或6 D.2或6
6.平面内互不重合的三条直线的交点个数是( )
A.1,3 B.0,1,3 C.0,2,3 D.0,1,2,3
7.平面内有两两相交的七条直线,若最多有m个交点,最少有n个交点,则m+n等于( )
A.16 B.22 C.20 D.18
8.下列说法: ①把弯曲的河道改直,能够缩短航程,这是由于两点之间线段最短; ②若线段AC=BC,则点C是线段AB的中点;③射线AB与射线AD是同一条射线;④ 连结两点的线段叫做这两点的距离;⑤将一根细木条固定在墙上,至少需要两根钉子,是因为两点确定一条直线.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
9.下列说法中,正确的个数为( )
①过同一平面内5点,最多可以确定9条直线; ②连接两点的线段叫做两点的距离; ③若AB=BC,则点B是线段AC的中点; ④三条直线两两相交,一定有3个交点.
A.3个 B.2个 C.1个 D.0个
10.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
【课后练习】答案
1.C 2.B 3.D 4.B 5.D 6.D 7.B 8.B 9.D 10.D
11.2或6
12.
13.18cm
14.13或3
15.3
4.2 直线、射线、线段
【学习目标】
1、了解射线的定义、射线的表示方法及特征.
2、会用尺规画一条线段等于已知线段;会利用直尺和圆规比较两条线段的长短;
3、明白线段中点概念,并会运用;明白并会应用“两点之间线段最短”性质。
【课前预习】
1.在直线 l 上取 A、B、C 三点,使得 AB=5 cm,BC=3 cm,如果点 O 是线段 AC 的中点,那么线段 OB 的长度是( )
A.4 cm B.1 cm C.1.5 cm D.1 cm 或 4 cm
2.下列语句正确的有( )
(1)线段AB就是A、B两点间的距离;(2)画射线AB=10cm;(3)A,B两点之间的所有连线中,最短的是线段AB;(4)在直线上取A,B,C三点,若AB=5cm,BC=2cm,则AC=7cm.
A.1个 B.2个 C.3个 D.4个
3.下列现象中,可用基本事实“两点之间,线段最短”来解释的现象是( )
A.用两个钉子就可以把木条固定在墙上 B.利用圆规可以比较两条线段的大小关系 C.把弯曲的公路改直,就能缩短路程 D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
4.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ).
A.1 B.2 C.1或2或3 D.0或1或2或3
5.在平面上有任意四个点,那么这四个点可以确定的直线有( )
A.1条 B.4条 C.6条 D.1条或4条或6条
【课前预习】答案
1.D
2.A
3.C
4.C
5.D
(1)经过一点O可以画几条直线?
(2)经过两点A、B可以画直线吗?可
以画几条?
画一画
·o
·A
·B
经过一点可以画无数条直线
经过两点能画直线,只能画一条。
经过两点有一条直线,并且只有一条直线
简述为:两点确定一条直线
直线的性质
生活中我们常常用到两点确定一条
直线,你能举几个例子吗?
植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
两点确定一条直线的应用:
两点确定一条直线的应用:
1、植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线。
建筑工人在砌墙时经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线, 根据 道理.
两点确定一条直线的
怎样用数学符号表示直线?
A
B
(2)我们还可以用一个小写字母来表示一条直线。
如下列直线记作直线l。
A
B
直线的表示方法
l
(1)我们用直线上的两个点来表示这条直线。
如下列直线记作直线AB或直线BA。
点和直线的关系
直线和直线的关系
ι
O
A
B
点O在直线ι上(直线ι经过点O);
点A、B 在直线ι外(直线 ι不经过点A 、B)。
a
b
O
直线a和b相交于点O
当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
O
A
B
表示:线段 AB(或线段BA)
a
表示:线段 a
A
表示:射线OA
表示:射线b
b
线段、射线的表示方法
线段: ①用两个端点的字母来表示,无先后顺序。可度量
②用一个小写字母表示。
射线: ① 用端点及射线上一点来表示,不可度量
注意端点的字母写在前面。
②用一个小写字母表示。
直线: ①用直线上两个点来表示,无先后顺序,不可度量。
②用一个小写字母来表示。
归纳总结
你发现直线、射线、线段有什么联系吗?又有什么区别呢?
发现
图形
表示方法
端点个数
延伸方向
线段
射线
直线
直线、射线、线段的联系与区别?
A
B
a
A
B
a
线段AB或线段a
射线AB或射线a
直线AB或直线a
两个
一个
0
不向任何一方延伸
向一方无限延伸
向两方无限延伸
A
B
a
注意:
(1)表示线段、射线、直线的时候,都要在字母前注明“线段” “射线 ” “直线”。
(2)用两个大写字母表示直线或线段时,两个字母可以交换位置,表示射线的两个大写
字母不能交换位置,必须把端点字母放在前面。
指出下图中线段、射线、直线分别有多少条?
A
B
C
答:
有3条线段,是线段 AB、线段 AC、线段 BC
有6条射线。
只有一条直线,是直线 AB或直线 BC或直线AC。
你会数吗?
点与直线的位置关系
点A在直线a外
点B在直线a上
点C在直线a外
a
A
B
C
直线 a 经过点 B
直线 a 不经过点 A
直线 a 不经过点 C
如图,分别过点A、C和点B、C画直线,所画的直线有怎样的位置关系?
·B
·C
A·
当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫做它们的交点
(1)经过一点O可以画几条直线?
(2)经过两点A、B可以画直线吗?可 以画几条?
探究
画一画
·o
·A
·B
经过一点可以画无数条直线
经过两点能画直线,只能画一条。
如果将细木条抽象成直线,将钉子抽象为点,你可以得出什么结论?
过两点有且只有一条直线。
简单说成:两点确定一条直线。
猜想
基本事实
实践乐园
植树节,同学要把一排树植整齐,怎么办?
只要定出两个树坑的位置就能
确定同一行的树坑所在的直线
实践乐园
建筑工人在砌墙时会在墙的两头分别固定两枚钉子,然后在钉子之间拉一条绳子,定出一条直的参照线,这样砌出的墙就是直的;同理木工师傅经过刨平的木板上的两个点,能弹出一条笔直的墨线
按语句画图:
2、点A在直线a外;
3、经过点O的三条线段a、b、c;
4、线段AB、CD相交于点B。
1、直线EF经过点C;
活动4
1、直线EF经过点C;
E
F
C
2、点A在直线a外;
a
A
3、经过点O的三条线段a、b、c;
a
b
c
O
4、线段AB、CD相交于点B。
A
B
C
D
1 .进一步认识了线段、射线和直线的概
念,知道了它们的表示方法。
2、探索出“经过两点有且只有一条直线”的性质,并了解其在生活中的运用,体会到数学就在我们身边。
谈谈你的收获
3.利用线段、射线和直线可以创造出很多美丽的图案,用它们可以美化我们的生活。
挑战:你能用线段、射线或直线
创造出美丽的图案吗?
发挥自己的想象,课后完成自己的创作。
【课后练习】
1.如果线段AB=5cm,BC=4cm,且A、B、C在同一条直线上,那么A、C两点间的距离是( )
A.1cm B.9cm C.1cm或9cm D.12cm
2.下列说法:
①过两点有且只有一条直线;②连接两点的线段叫两点的距离;③两点之间线段最短;④如果AB=BC,则点B是AC的中点.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.点 A、B、C 在同一条数轴上,其中点 A、B 表示的数分别为﹣3、1,若 BC=2,则 AC 等于( )
A.3 B.2 C.3 或 5 D.2 或 6
4.下列生活、生产现象:①用两颗钉子就可以把木条固定在墙上;②从甲地到乙地架设电线,总是沿线段架设;③把弯曲的公路改直就能缩短路程;④植树时只要确定两棵树的位置,就能确定同一行树所在的直线.其中能用“两点之间线段最短”来解释的现象是( )
A.①② B.②③ C.①④ D.③④
5.已知线段AB,C是直线AB上的一点,AB=8,BC=4,点M是线段AC的中点,则线段AM的长为( )
A.2 B.4 C.4或6 D.2或6
6.平面内互不重合的三条直线的交点个数是( )
A.1,3 B.0,1,3 C.0,2,3 D.0,1,2,3
7.平面内有两两相交的七条直线,若最多有m个交点,最少有n个交点,则m+n等于( )
A.16 B.22 C.20 D.18
8.下列说法: ①把弯曲的河道改直,能够缩短航程,这是由于两点之间线段最短; ②若线段AC=BC,则点C是线段AB的中点;③射线AB与射线AD是同一条射线;④ 连结两点的线段叫做这两点的距离;⑤将一根细木条固定在墙上,至少需要两根钉子,是因为两点确定一条直线.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
9.下列说法中,正确的个数为( )
①过同一平面内5点,最多可以确定9条直线; ②连接两点的线段叫做两点的距离; ③若AB=BC,则点B是线段AC的中点; ④三条直线两两相交,一定有3个交点.
A.3个 B.2个 C.1个 D.0个
10.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
【课后练习】答案
1.C 2.B 3.D 4.B 5.D 6.D 7.B 8.B 9.D 10.D
11.2或6
12.
13.18cm
14.13或3
15.3
