人教版七年级数学上册教学课件-4.3.3余角和补角(共28张ppt)
文档属性
| 名称 | 人教版七年级数学上册教学课件-4.3.3余角和补角(共28张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 12:03:26 | ||
图片预览






文档简介
观赏意大利名胜比萨斜塔
1
2
1和 2有什么关系?
1、提出问题,创设情景:
2
1
1和 2有什么关系?
3
4
3和 4有什么关系?
4
3和 4有什么关系?
3
余角与补角
余角与补角
1
2
,就说这两个角
3
4
互为余角
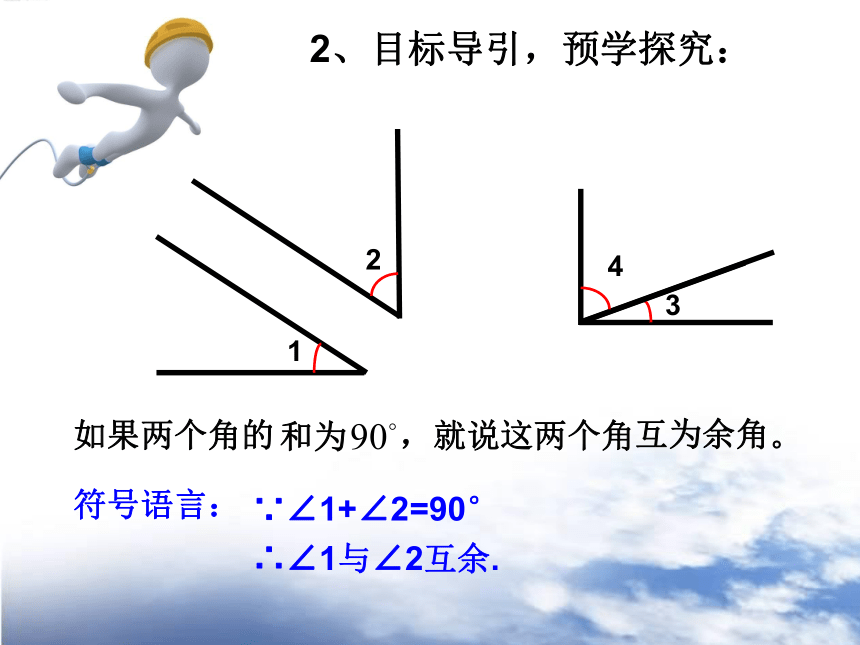
如果两个角的
和为
。
2、目标导引,预学探究:
符号语言:
∵∠1+∠2=90°
∴∠1与∠2互余.
2
1
3
4
,就说这两个角
互为补角
如果两个角的
和为
。
符号语言:
∵∠1+∠2=180°
∴∠1与∠2互补.
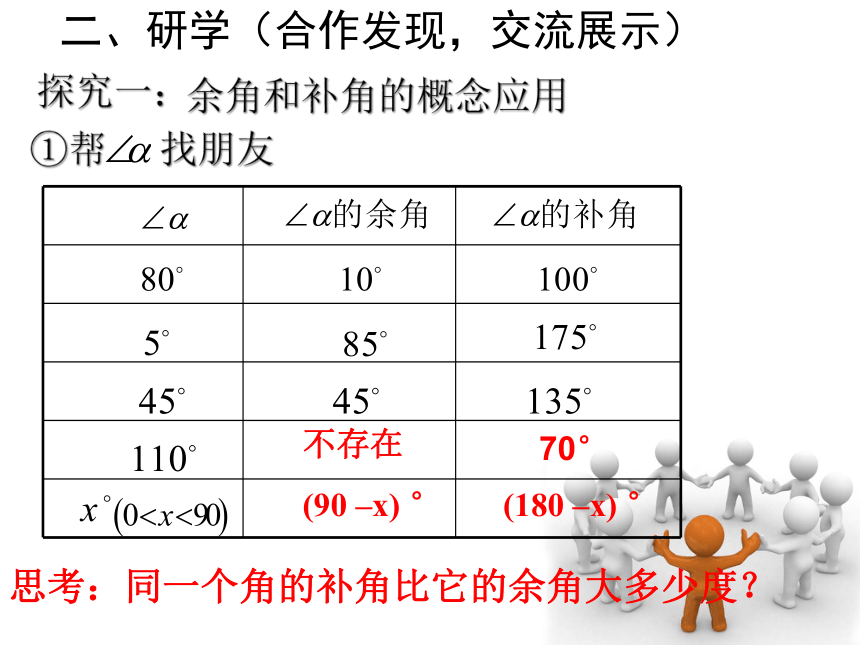
①帮 找朋友
二、研学(合作发现,交流展示)
探究一:
思考:同一个角的补角比它的余角大多少度?
余角和补角的概念应用
不存在
70°
(90 –x) °
(180 –x) °
探究一:
一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
解:设这个角的度数为 ,则依题意得
答:这个角的余角的度数为
另解:设这个角的余角的度数为 ,
则它的补角可设为
答:这个角的余角的度数为
②用心算一算
余角和补角的概念应用
B
A
O
C
如图两面墙围一个角 ,但人不能进入围墙内,我们如何去测量这个角的大小呢?
动动脑
看看谁反应快!
D
B
A
O
C
动动脑
D
探究二:
2
3
1
观察发现 和 互补, 和 互补,那 和 相等吗?
同角的补角相等.
补角性质:
几何语言:
余角和补角的性质
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
等角的补角相等.
补角性质:
几何语言:
探究二:
余角和补角的性质
补角性质:同角(等角)的补角相等.
1
2
3
余角性质:
几何语言:
探究二:
余角和补角的性质
同角的余角相等.
如图∠1 与∠2互余,∠2 与∠3互余 ,那么∠1与∠3相等吗?为什么?
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
等角的余角相等.
余角性质:
几何语言:
探究二:
余角和补角的性质
余角性质:同角(等角)的余角相等.
同角(等角)的余角相等.
若∠1+∠2=90°,∠1+∠3=90°;
则∠2=∠3.
同角(等角)的补角相等.
若∠1+∠2=180°,∠1+∠3=180°;
则∠2=∠3.
余角和补角的性质
如图,已知∠AOC=∠BOD=90°,∠COD=30°
求:①∠AOD= ,∠BOC= .
∠AOD和∠BOC有什么数量关系?
②∠AOB= .
∠COD和∠AOB有什么数量关系?
A
O
B
C
D
60°
60°
150°
∠COD+∠AOB=180°
相等
探究三:
余角和补角性质的应用
A
O
B
C
D
如下图,已知∠AOC=∠BOD=90°,∠COD=∠ .
猜想:
①∠AOD和∠BOC还相等吗?并说明理由.
②∠COD与∠AOB有什么数量关系,并说明理由.
E
A
O
B
C
D
应用:已知∠AOC=∠BOD=90°,
∠AOB=120°,则∠COD= .
若∠AOB=∠ ,则∠COD= .
60°
互余
互补
对应图形
数量关系
性质
小结
同角(等角)的余角相等。
同角(等角)的补角相等。
互余、互补是两角之间的数量关系,只与他们的度数和有关,与位置无关。
1
互余、互补概念中的角是成对出现的。
2
只有锐角才有余角。
4
注意点
角 的余角是 ,补角是
同一个锐角的补角比余角大
3
完成小作业第57面。
1
预习课本第138面例4
并完成导学案第102面。
2
1
3
4
游戏规则: 每个小组从5个金蛋中任选一个,回答金蛋中的问题,答对则加3分,答错或不答者不加分,若本组答错,则其他组的成员有机会回答,此时答对者所在的组奖励3分。
2
5
探究X:
(1)从图中找出两对互余的角?
∠A与∠B互余 ∠A与∠2互余
∠1与∠B互余 ∠1与∠2互余
B
A
D
C
1
2
认真观察下面的图形,回答下列问题:
1.∠1+∠2+∠3=90°, ∠1、 ∠2、∠3互余。
( )
2.互补的两个角,一定一个是锐角,一个是钝角。
( )
判断题:
×
×
下列各图中,∠1 与∠2互为余角的是( )
2
1
2
1
2
1
2
1
A
B
C
D
C
恭喜你,你们组运气很好哦,不用作答,加3分!
如图∠AOC= ∠BOC=∠DOE=90°,则
(1) 图中与∠3互余的角是_________,
(2)图中与∠2互补的角是_________.
∠2
,∠4
∠AOE
1
2
1和 2有什么关系?
1、提出问题,创设情景:
2
1
1和 2有什么关系?
3
4
3和 4有什么关系?
4
3和 4有什么关系?
3
余角与补角
余角与补角
1
2
,就说这两个角
3
4
互为余角
如果两个角的
和为
。
2、目标导引,预学探究:
符号语言:
∵∠1+∠2=90°
∴∠1与∠2互余.
2
1
3
4
,就说这两个角
互为补角
如果两个角的
和为
。
符号语言:
∵∠1+∠2=180°
∴∠1与∠2互补.
①帮 找朋友
二、研学(合作发现,交流展示)
探究一:
思考:同一个角的补角比它的余角大多少度?
余角和补角的概念应用
不存在
70°
(90 –x) °
(180 –x) °
探究一:
一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
解:设这个角的度数为 ,则依题意得
答:这个角的余角的度数为
另解:设这个角的余角的度数为 ,
则它的补角可设为
答:这个角的余角的度数为
②用心算一算
余角和补角的概念应用
B
A
O
C
如图两面墙围一个角 ,但人不能进入围墙内,我们如何去测量这个角的大小呢?
动动脑
看看谁反应快!
D
B
A
O
C
动动脑
D
探究二:
2
3
1
观察发现 和 互补, 和 互补,那 和 相等吗?
同角的补角相等.
补角性质:
几何语言:
余角和补角的性质
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
等角的补角相等.
补角性质:
几何语言:
探究二:
余角和补角的性质
补角性质:同角(等角)的补角相等.
1
2
3
余角性质:
几何语言:
探究二:
余角和补角的性质
同角的余角相等.
如图∠1 与∠2互余,∠2 与∠3互余 ,那么∠1与∠3相等吗?为什么?
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
等角的余角相等.
余角性质:
几何语言:
探究二:
余角和补角的性质
余角性质:同角(等角)的余角相等.
同角(等角)的余角相等.
若∠1+∠2=90°,∠1+∠3=90°;
则∠2=∠3.
同角(等角)的补角相等.
若∠1+∠2=180°,∠1+∠3=180°;
则∠2=∠3.
余角和补角的性质
如图,已知∠AOC=∠BOD=90°,∠COD=30°
求:①∠AOD= ,∠BOC= .
∠AOD和∠BOC有什么数量关系?
②∠AOB= .
∠COD和∠AOB有什么数量关系?
A
O
B
C
D
60°
60°
150°
∠COD+∠AOB=180°
相等
探究三:
余角和补角性质的应用
A
O
B
C
D
如下图,已知∠AOC=∠BOD=90°,∠COD=∠ .
猜想:
①∠AOD和∠BOC还相等吗?并说明理由.
②∠COD与∠AOB有什么数量关系,并说明理由.
E
A
O
B
C
D
应用:已知∠AOC=∠BOD=90°,
∠AOB=120°,则∠COD= .
若∠AOB=∠ ,则∠COD= .
60°
互余
互补
对应图形
数量关系
性质
小结
同角(等角)的余角相等。
同角(等角)的补角相等。
互余、互补是两角之间的数量关系,只与他们的度数和有关,与位置无关。
1
互余、互补概念中的角是成对出现的。
2
只有锐角才有余角。
4
注意点
角 的余角是 ,补角是
同一个锐角的补角比余角大
3
完成小作业第57面。
1
预习课本第138面例4
并完成导学案第102面。
2
1
3
4
游戏规则: 每个小组从5个金蛋中任选一个,回答金蛋中的问题,答对则加3分,答错或不答者不加分,若本组答错,则其他组的成员有机会回答,此时答对者所在的组奖励3分。
2
5
探究X:
(1)从图中找出两对互余的角?
∠A与∠B互余 ∠A与∠2互余
∠1与∠B互余 ∠1与∠2互余
B
A
D
C
1
2
认真观察下面的图形,回答下列问题:
1.∠1+∠2+∠3=90°, ∠1、 ∠2、∠3互余。
( )
2.互补的两个角,一定一个是锐角,一个是钝角。
( )
判断题:
×
×
下列各图中,∠1 与∠2互为余角的是( )
2
1
2
1
2
1
2
1
A
B
C
D
C
恭喜你,你们组运气很好哦,不用作答,加3分!
如图∠AOC= ∠BOC=∠DOE=90°,则
(1) 图中与∠3互余的角是_________,
(2)图中与∠2互补的角是_________.
∠2
,∠4
∠AOE
