人教版数学九年级上册 25.2用列表法求概率 教学课件(共14张ppt)
文档属性
| 名称 | 人教版数学九年级上册 25.2用列表法求概率 教学课件(共14张ppt) | 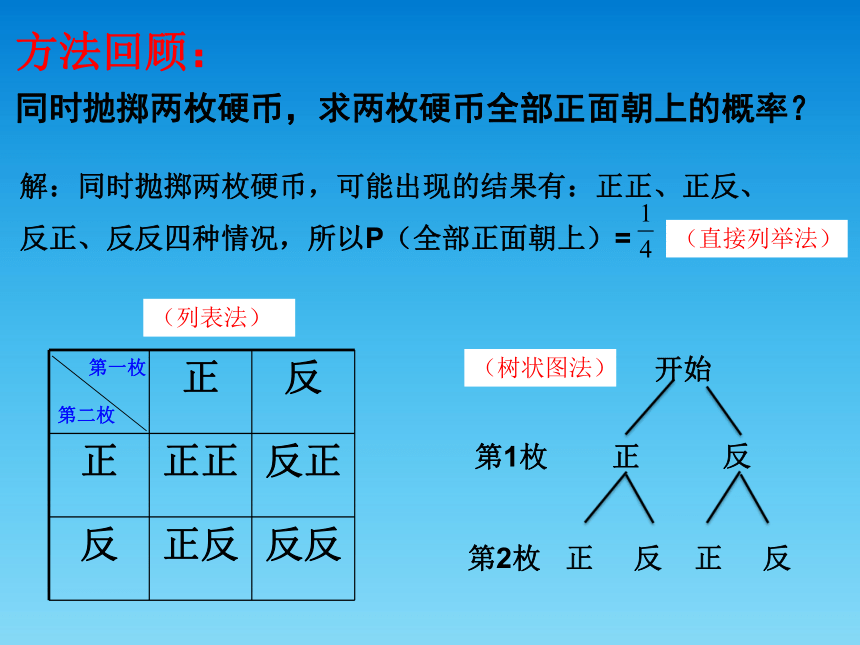 | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 12:04:52 | ||
图片预览







文档简介
方法回顾:
同时抛掷两枚硬币,求两枚硬币全部正面朝上的概率?
(直接列举法)
解:同时抛掷两枚硬币,可能出现的结果有:正正、正反、反正、反反四种情况,所以P(全部正面朝上)=
开始
第1枚 正
反
第2枚 正 反 正 反
(树状图法)
正
反
正
正正
反正
反
正反
反反
第一枚
第二枚
(列表法)
日常生活中的概率问题
学习目标:
1、能正确运用列举法解决日常生活中的概率问题
2、能通过比较概率的大小,在决策问题中做出更佳决策
3、能对日常生活中一些游戏活动的公平性做出评判
例1:小娟是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小娟正好穿的是相同的一双袜子的概率是多少?
例1:
解:设两双袜子分别为A1、A2、B1、B2,则
得一超市为了吸引顾客,准备了两个不透明的箱子,甲箱中放着24只红球和16只黑球,乙箱中则放着200只红球,80只黑球和10只白球,这三种球除了颜色以外没有任何区别。两个箱子中的球都已经各自搅匀。
超市规定:顾客每购买100元商品,就能获得一次摸球机会,蒙上眼睛从箱子中取一只球,如果取出1只黑球,则获得50元购物券,那么选哪个箱子成功的机会大呢?
决策问题
例2:
得一超市为了吸引顾客,准备了两个不透明的箱子,甲箱中放着24只红球和16只黑球,乙箱中则放着200只红球,80只黑球和10只白球,这三种球除了颜色以外没有任何区别。两个箱子中的球都已经各自搅匀。
超市规定:顾客每购买100元商品,就能获得一次摸球机会,蒙上眼睛从箱子中取一只球,如果取出1只黑球,则获得50元购物券,那么选哪个箱子成功的机会大呢?
决策问题
例2:
这个游戏对小健公平吗?
小聪和小健做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4
例3:
你能求出小健得分的概率吗?
小聪:“我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,积为偶数我得1分,先得到10分的获胜”。
小健:我该不该接受挑战呢?
1
2
3
4
1
2
3
4
红桃
黑桃
用表格表示
(1,1)
(2,1)
(3,1)
(4,1)
(1,2)
(2,2)
(3,2)
(4,2)
(1,3)
(2,3)
(3,3)
(4,3)
(1,4)
(2,4)
(3,4)
(4,4)
解:满足两张牌的数字之积为奇数的有(1,1)(1,3)(3,1)(3,3),这4种情况,所以
P(数字之积为奇数)=
P(数字之积为偶数)=
因为P(奇)≠P(偶),所以这个游戏对小健不公平
规则2:若两次转出的数字之积为偶数,则小锤赢;反之,则狗蛋赢(第3、4小组完成)
1
2
不公平,对小锤有利
规则3:若两次转出的数字组成的两位数大于40,则小锤赢;反之,则狗蛋赢(第5、6小组完成)
不公平,对狗蛋有利
不公平,对狗蛋有利
你能否为狗蛋和锤子设定一个公平的游戏规则呢?
A
2、小明和小亮做游戏,先是各自背着对方在纸上写一个不大于100的正整数,然后都拿给对方看。他们约定:若两人所写的数都是奇数或都是偶数,则小明获胜;若两个人所写的数一个是奇数,另一个是偶数,则小亮获胜。这个游戏( )
A.对小明有利 B.对小亮有利 C.是公平的 D.无法确定对谁有利
C
1、能正确运用列举法解决日常生活中的概率问题
(直接列举法、列表法、树状图法)
2、能通过比较概率的大小,在决策问题中作出更佳决策
(求出不同选择的概率——比较——做出决策)
3、能对日常生活中一些游戏活动的公平性做出评判
(先求概率——判断——①若 P(A)=P(B),则游戏公平;
②若P(A)≠P(B),则游戏不公平)
熙熙攘攘的集市上,某人在设摊“摸彩”,只见他手拿一袋,内装大小、形状、质量完全相同的4个绿球和4个红球,每次让“顾客”免费从袋中摸出4个球,输赢的规则是:
只见很多顾客围上前去,“免费”摸球,而且只有摸到“2红2绿”的情况才赔钱,其余情况都能得钱。而我在旁边观察的结果有一半以上的人都赔了钱,这种活动的欺骗性到底体现在什么地方呢?相信同学们经过这节课的学习
定能揭开其中的“奥秘”,而不愿参加这一“免费”活动,变得更加智慧。
所摸球的颜色
顾客的收益
4个全红
得50元
3红1绿
得50元
2红2绿
失30元
1红3绿
得20元
4个全绿
得50元
同时抛掷两枚硬币,求两枚硬币全部正面朝上的概率?
(直接列举法)
解:同时抛掷两枚硬币,可能出现的结果有:正正、正反、反正、反反四种情况,所以P(全部正面朝上)=
开始
第1枚 正
反
第2枚 正 反 正 反
(树状图法)
正
反
正
正正
反正
反
正反
反反
第一枚
第二枚
(列表法)
日常生活中的概率问题
学习目标:
1、能正确运用列举法解决日常生活中的概率问题
2、能通过比较概率的大小,在决策问题中做出更佳决策
3、能对日常生活中一些游戏活动的公平性做出评判
例1:小娟是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小娟正好穿的是相同的一双袜子的概率是多少?
例1:
解:设两双袜子分别为A1、A2、B1、B2,则
得一超市为了吸引顾客,准备了两个不透明的箱子,甲箱中放着24只红球和16只黑球,乙箱中则放着200只红球,80只黑球和10只白球,这三种球除了颜色以外没有任何区别。两个箱子中的球都已经各自搅匀。
超市规定:顾客每购买100元商品,就能获得一次摸球机会,蒙上眼睛从箱子中取一只球,如果取出1只黑球,则获得50元购物券,那么选哪个箱子成功的机会大呢?
决策问题
例2:
得一超市为了吸引顾客,准备了两个不透明的箱子,甲箱中放着24只红球和16只黑球,乙箱中则放着200只红球,80只黑球和10只白球,这三种球除了颜色以外没有任何区别。两个箱子中的球都已经各自搅匀。
超市规定:顾客每购买100元商品,就能获得一次摸球机会,蒙上眼睛从箱子中取一只球,如果取出1只黑球,则获得50元购物券,那么选哪个箱子成功的机会大呢?
决策问题
例2:
这个游戏对小健公平吗?
小聪和小健做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4
例3:
你能求出小健得分的概率吗?
小聪:“我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,积为偶数我得1分,先得到10分的获胜”。
小健:我该不该接受挑战呢?
1
2
3
4
1
2
3
4
红桃
黑桃
用表格表示
(1,1)
(2,1)
(3,1)
(4,1)
(1,2)
(2,2)
(3,2)
(4,2)
(1,3)
(2,3)
(3,3)
(4,3)
(1,4)
(2,4)
(3,4)
(4,4)
解:满足两张牌的数字之积为奇数的有(1,1)(1,3)(3,1)(3,3),这4种情况,所以
P(数字之积为奇数)=
P(数字之积为偶数)=
因为P(奇)≠P(偶),所以这个游戏对小健不公平
规则2:若两次转出的数字之积为偶数,则小锤赢;反之,则狗蛋赢(第3、4小组完成)
1
2
不公平,对小锤有利
规则3:若两次转出的数字组成的两位数大于40,则小锤赢;反之,则狗蛋赢(第5、6小组完成)
不公平,对狗蛋有利
不公平,对狗蛋有利
你能否为狗蛋和锤子设定一个公平的游戏规则呢?
A
2、小明和小亮做游戏,先是各自背着对方在纸上写一个不大于100的正整数,然后都拿给对方看。他们约定:若两人所写的数都是奇数或都是偶数,则小明获胜;若两个人所写的数一个是奇数,另一个是偶数,则小亮获胜。这个游戏( )
A.对小明有利 B.对小亮有利 C.是公平的 D.无法确定对谁有利
C
1、能正确运用列举法解决日常生活中的概率问题
(直接列举法、列表法、树状图法)
2、能通过比较概率的大小,在决策问题中作出更佳决策
(求出不同选择的概率——比较——做出决策)
3、能对日常生活中一些游戏活动的公平性做出评判
(先求概率——判断——①若 P(A)=P(B),则游戏公平;
②若P(A)≠P(B),则游戏不公平)
熙熙攘攘的集市上,某人在设摊“摸彩”,只见他手拿一袋,内装大小、形状、质量完全相同的4个绿球和4个红球,每次让“顾客”免费从袋中摸出4个球,输赢的规则是:
只见很多顾客围上前去,“免费”摸球,而且只有摸到“2红2绿”的情况才赔钱,其余情况都能得钱。而我在旁边观察的结果有一半以上的人都赔了钱,这种活动的欺骗性到底体现在什么地方呢?相信同学们经过这节课的学习
定能揭开其中的“奥秘”,而不愿参加这一“免费”活动,变得更加智慧。
所摸球的颜色
顾客的收益
4个全红
得50元
3红1绿
得50元
2红2绿
失30元
1红3绿
得20元
4个全绿
得50元
同课章节目录
