人教版数学九年级上册24.2.1反证法课件(共17张ppt)
文档属性
| 名称 | 人教版数学九年级上册24.2.1反证法课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 12:06:08 | ||
图片预览





文档简介
24.2.1 反证法
2011人教课标版·中学数学 ·九年级上册
2.构成:
(1)每个命题都有题设、结论两部分组成
(2)命题常写成“如果……那么……”
的形式
回顾复习
1.命题:判断一件事情的语句
3.分类:
(1)真命题:正确的命题
(2)假命题:错误的命题
问题情境
晓娟睡觉前,地上是干的,早晨起来,看见地上全湿了。晓娟对小晶说:“昨天晚上下雨了。”
你能对晓娟的判断说出理由吗?
晓娟的理由:
假设昨天晚上没有下雨,那么地上应是干的,这与早晨地上全湿了相矛盾,所以说昨晚下雨是正确的。
思考:
我们可以把这种推理方
法应用到数学问题上吗?
了解反证法
反证法的定义:
在证明数学问题时,先假定命题结论的反面成立,在这个前提下,若推出的结果与定义、公理、定理相矛盾,或与命题中的已知条件相矛盾,或与假定相矛盾,从而说明命题结论的反面不可能成立,由此断定命题的结论成立,这种证明方法叫作反证法。
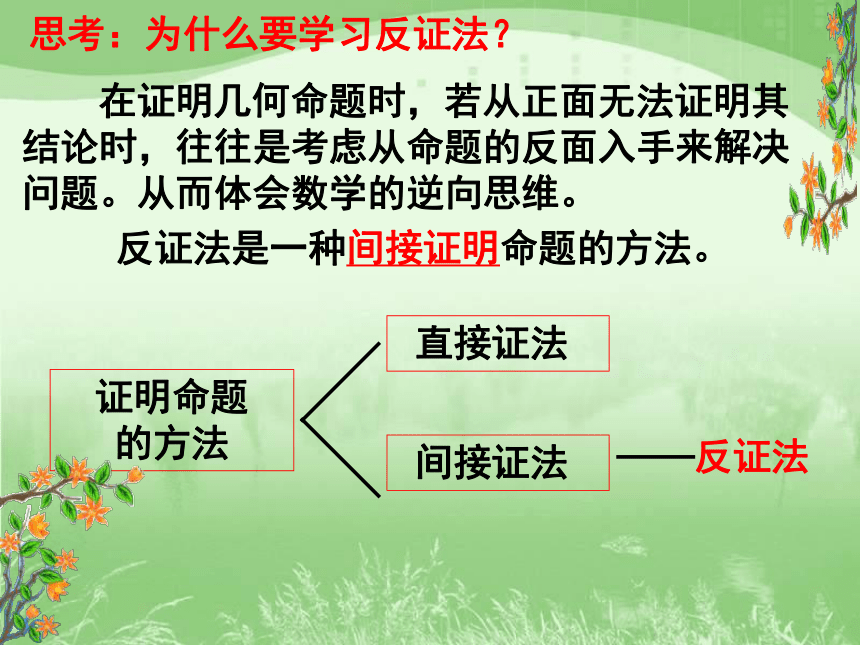
证明命题 的方法
直接证法
间接证法
反证法
思考:为什么要学习反证法?
在证明几何命题时,若从正面无法证明其结论时,往往是考虑从命题的反面入手来解决问题。从而体会数学的逆向思维。
反证法是一种间接证明命题的方法。
反证法的证题步骤:
(1)假设结论的反面成立;
(2)从这个假设出发,经过推理论证,得出矛盾;
(3)由假设不正确,从而命题的结论成立
一、你能用更简洁的文字概括反证法的基本步骤吗?
二、反证法在推理中可能得出哪几类矛盾?
深入认识反证法
(1)反设
(2)归谬
(3)结论
与已知条件相矛盾或与公理、定理、定义或与假定相矛盾
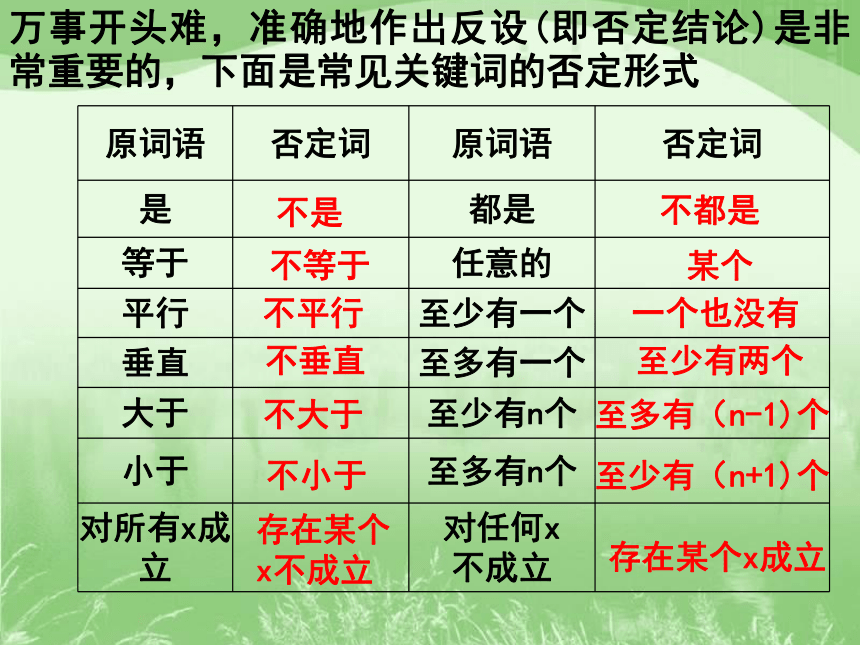
原词语
否定词
原词语
否定词
是
都是
等于
任意的
平行
至少有一个
垂直
至多有一个
大于
至少有n个
小于
至多有n个
对所有x成立
对任何x
不成立
不是
不等于
不平行
不垂直
不大于
不小于
存在某个x不成立
不都是
某个
一个也没有
至少有两个
至多有(n-1)个
至少有(n+1)个
存在某个x成立
万事开头难,准确地作出反设(即否定结论)是非常重要的,下面是常见关键词的否定形式 ?
典例析解
在△ABC中,若∠C是直角,那么∠B一定是锐角.
分析:显然命题的结论是正确的,但直接证明是较困难的,而用反证法就容易证明了。
请你思考第一步应该如何做?
证明:
假设∠B是直角,
因∠C是直角,所以∠C+∠B=180°,
此时∠A=0°,这与三角形的内角和定理矛盾,
所以∠B为锐角.
这个证明推理完整吗?
已知:在△ABC中,∠C=90°.求证: ∠B一定是锐角.
证明:假设∠B不是锐角,即∠B是直角或钝角.
综合① 和②知假设不成立,
所以∠B一定是锐角.
①当∠B是直角,即∠B= 90°时,
②当∠B是钝角,即∠B > 90°时,
∠B+∠C=90°+90°=180°,
于是∠ A+∠B+∠C=∠A +180°>180°,
这与三角形的内角和等于180°相矛盾;
∠B+ ∠C > 90°+90°=180°,
于是∠ A+∠B+∠C>∠A +180°>180°,
这与三角形的内角和等于180°相矛盾;
A
C
B
用反证法证题时,应注意的事项 :
??
(1)防止否定不当或有所遗漏;
(2)推理过程必须完整;
(3)在推理过程中,要充分使用已知条
件,否则推不出矛盾,或者不能断
定推出的结果是错误的。
已知:在△ABC中, ∠A≠∠B≠∠C
求证:△ABC不是等腰三角形.
(1)当AB=AC时,
∴∠B=∠C(等边对等角)
这与已知条件∠B≠∠C矛盾
如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形。
A
B
C
(1)反设
(2)归谬
(3)结论
证明:
假设△ABC是等腰三角形
假设不成立
∴ △ABC不是等腰三角形
(2)当AB=BC时呢?
(3)当AC=BC时呢?
已知:如图△ABC中,D、E两点分别在AB和AC上
求证:CD、BE不能互相平分
(平行四边形对边平行)
做一做
假设CD、BE互相平分
连结DE,故四边形BCED是平行四边形
∴BD∥CE
这与BD、CE交于点A矛盾
假设错误,
∴CD、BE不能互相平分
证明:
(2)归谬
(3)结论
(1)反设
课时作业设计
2.已知:如图有a、b、c三条直线,且a//c,b//c.
求证:a//b
a
b
c
3.求证:三角形内角中至多有一个内角是钝角。
1.在一个三角形中,如果两条边不等,那么它们所对的角也不等。
大家议一议!
哪些问题适
宜用反证法
我来告诉你
1.存在性问题;
2.否定性问题;
3.唯一性问题;
4.至多、至少类问题;
5.一些基本命题、基本定理定理的 逆命题;
6.解决整除性问题;
7.一些不等量命题的证明;
8.涉及各种“无限”结论的命题。
总之,直接证明比较困难的命题
证明命题 的方法
直接证法
间接证法
反证法
回顾与归纳
1、这节课你有什么收获?
假设结论的反面正确
推理论证
得出结论
(1)反设
(2)归谬
(3)结论
得出矛盾(与已知、
公理、定理等)
假设不成立,
原命题成立.
2、反证法的一般步骤:
再见
2011人教课标版·中学数学 ·九年级上册
2.构成:
(1)每个命题都有题设、结论两部分组成
(2)命题常写成“如果……那么……”
的形式
回顾复习
1.命题:判断一件事情的语句
3.分类:
(1)真命题:正确的命题
(2)假命题:错误的命题
问题情境
晓娟睡觉前,地上是干的,早晨起来,看见地上全湿了。晓娟对小晶说:“昨天晚上下雨了。”
你能对晓娟的判断说出理由吗?
晓娟的理由:
假设昨天晚上没有下雨,那么地上应是干的,这与早晨地上全湿了相矛盾,所以说昨晚下雨是正确的。
思考:
我们可以把这种推理方
法应用到数学问题上吗?
了解反证法
反证法的定义:
在证明数学问题时,先假定命题结论的反面成立,在这个前提下,若推出的结果与定义、公理、定理相矛盾,或与命题中的已知条件相矛盾,或与假定相矛盾,从而说明命题结论的反面不可能成立,由此断定命题的结论成立,这种证明方法叫作反证法。
证明命题 的方法
直接证法
间接证法
反证法
思考:为什么要学习反证法?
在证明几何命题时,若从正面无法证明其结论时,往往是考虑从命题的反面入手来解决问题。从而体会数学的逆向思维。
反证法是一种间接证明命题的方法。
反证法的证题步骤:
(1)假设结论的反面成立;
(2)从这个假设出发,经过推理论证,得出矛盾;
(3)由假设不正确,从而命题的结论成立
一、你能用更简洁的文字概括反证法的基本步骤吗?
二、反证法在推理中可能得出哪几类矛盾?
深入认识反证法
(1)反设
(2)归谬
(3)结论
与已知条件相矛盾或与公理、定理、定义或与假定相矛盾
原词语
否定词
原词语
否定词
是
都是
等于
任意的
平行
至少有一个
垂直
至多有一个
大于
至少有n个
小于
至多有n个
对所有x成立
对任何x
不成立
不是
不等于
不平行
不垂直
不大于
不小于
存在某个x不成立
不都是
某个
一个也没有
至少有两个
至多有(n-1)个
至少有(n+1)个
存在某个x成立
万事开头难,准确地作出反设(即否定结论)是非常重要的,下面是常见关键词的否定形式 ?
典例析解
在△ABC中,若∠C是直角,那么∠B一定是锐角.
分析:显然命题的结论是正确的,但直接证明是较困难的,而用反证法就容易证明了。
请你思考第一步应该如何做?
证明:
假设∠B是直角,
因∠C是直角,所以∠C+∠B=180°,
此时∠A=0°,这与三角形的内角和定理矛盾,
所以∠B为锐角.
这个证明推理完整吗?
已知:在△ABC中,∠C=90°.求证: ∠B一定是锐角.
证明:假设∠B不是锐角,即∠B是直角或钝角.
综合① 和②知假设不成立,
所以∠B一定是锐角.
①当∠B是直角,即∠B= 90°时,
②当∠B是钝角,即∠B > 90°时,
∠B+∠C=90°+90°=180°,
于是∠ A+∠B+∠C=∠A +180°>180°,
这与三角形的内角和等于180°相矛盾;
∠B+ ∠C > 90°+90°=180°,
于是∠ A+∠B+∠C>∠A +180°>180°,
这与三角形的内角和等于180°相矛盾;
A
C
B
用反证法证题时,应注意的事项 :
??
(1)防止否定不当或有所遗漏;
(2)推理过程必须完整;
(3)在推理过程中,要充分使用已知条
件,否则推不出矛盾,或者不能断
定推出的结果是错误的。
已知:在△ABC中, ∠A≠∠B≠∠C
求证:△ABC不是等腰三角形.
(1)当AB=AC时,
∴∠B=∠C(等边对等角)
这与已知条件∠B≠∠C矛盾
如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形。
A
B
C
(1)反设
(2)归谬
(3)结论
证明:
假设△ABC是等腰三角形
假设不成立
∴ △ABC不是等腰三角形
(2)当AB=BC时呢?
(3)当AC=BC时呢?
已知:如图△ABC中,D、E两点分别在AB和AC上
求证:CD、BE不能互相平分
(平行四边形对边平行)
做一做
假设CD、BE互相平分
连结DE,故四边形BCED是平行四边形
∴BD∥CE
这与BD、CE交于点A矛盾
假设错误,
∴CD、BE不能互相平分
证明:
(2)归谬
(3)结论
(1)反设
课时作业设计
2.已知:如图有a、b、c三条直线,且a//c,b//c.
求证:a//b
a
b
c
3.求证:三角形内角中至多有一个内角是钝角。
1.在一个三角形中,如果两条边不等,那么它们所对的角也不等。
大家议一议!
哪些问题适
宜用反证法
我来告诉你
1.存在性问题;
2.否定性问题;
3.唯一性问题;
4.至多、至少类问题;
5.一些基本命题、基本定理定理的 逆命题;
6.解决整除性问题;
7.一些不等量命题的证明;
8.涉及各种“无限”结论的命题。
总之,直接证明比较困难的命题
证明命题 的方法
直接证法
间接证法
反证法
回顾与归纳
1、这节课你有什么收获?
假设结论的反面正确
推理论证
得出结论
(1)反设
(2)归谬
(3)结论
得出矛盾(与已知、
公理、定理等)
假设不成立,
原命题成立.
2、反证法的一般步骤:
再见
同课章节目录
