人教版数学九年级上册24.2.2切线的概念、切线的判定与性质课件(20张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.2.2切线的概念、切线的判定与性质课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 177.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览





文档简介
直线和圆的位置关系(2)
人教版九年级上册
温故知新
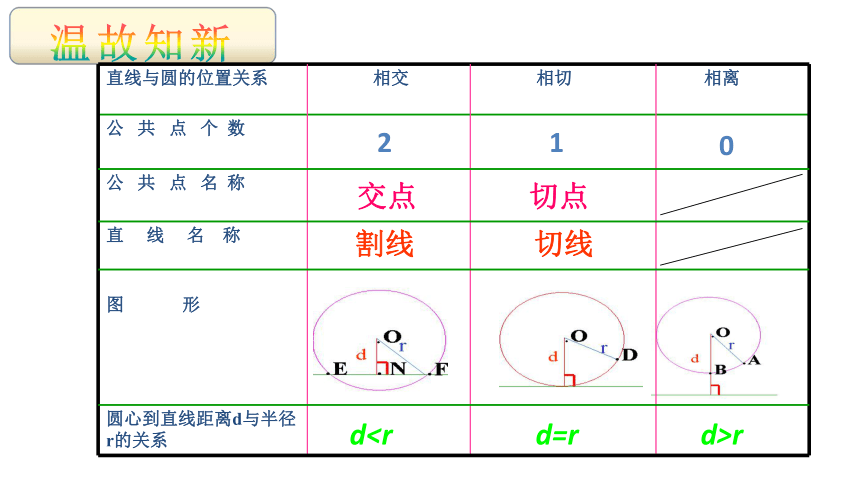
1.直线和圆有哪些位置关系?
温故知新
直线与圆的位置关系
相交
相切
相离
公 共 点 个 数
公 共 点 名 称
直 线 名 称
图 形
圆心到直线距离d与半径r的关系
dd=r
d>r
2
交点
割线
1
切点
切线
0
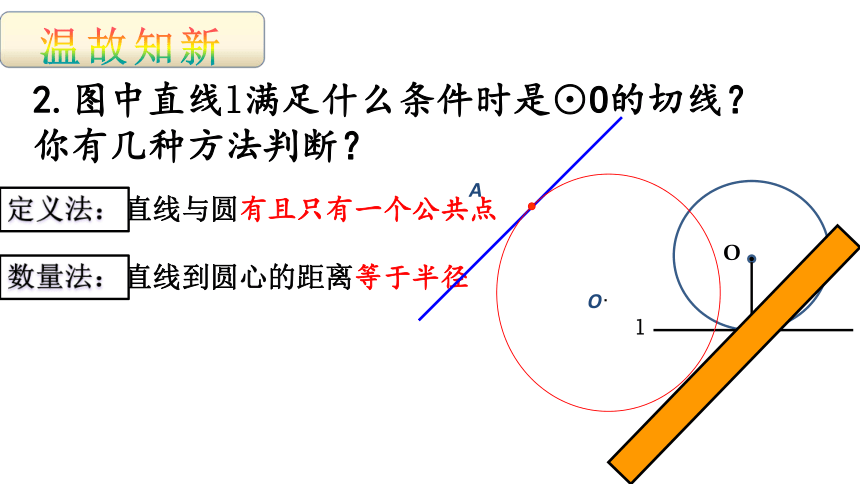
2.图中直线l满足什么条件时是⊙O的切线?你有几种方法判断?
O
方法一:直线与圆有且只有一个公共点
方法二:直线到圆心的距离等于半径
l
温故知新
A
O·
定义法:
数量法:
§24.2.2切线的判定定理
操作:
动手操作:
请在⊙O上任取一点A,连接OA,经过半径OA的外端点A作直线l⊥OA。
O
.
A
发现:
(1)直线l经过半径OA的
(2)直线l与半径OA
总结:直线l与⊙O的位置关系是
外端点A
垂直
相切
即直线l是⊙O的切线
O
.
A
切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两条: ①经过半径外端; ②垂直于这条半径
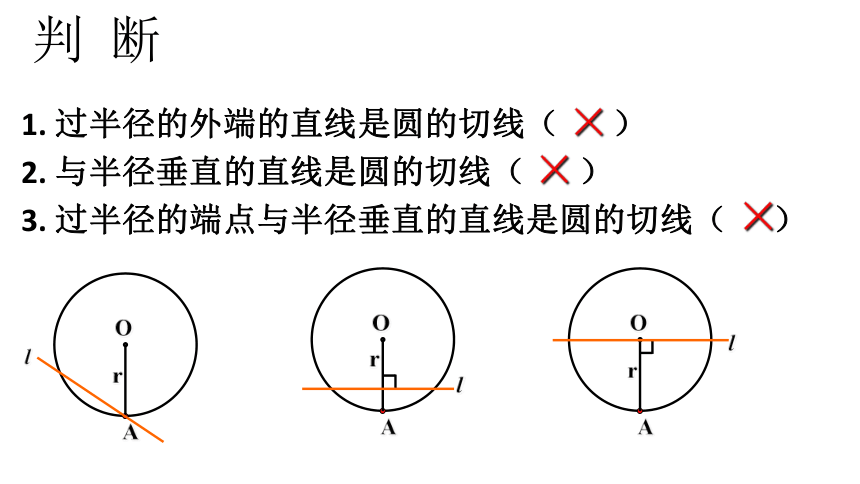
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
归纳:
判定直线与圆相切有哪些方法?
例题1
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连接OC(如图)。
∵ OA=OB
∴△AOC是等腰三角形
∵CA=CB
∴ OC是等腰三角形OAB底边AB上的中线
∴ AB⊥OC
∵ OC是⊙O的半径
∴ AB是⊙O的切线
有公共点,连半径,证垂直
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
例题2
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC OD⊥AB OE⊥AC
∴ OE=OD
∵ OD是⊙O的半径
∴OE是⊙O的半径
∴ AC是⊙O的切线。
O
A
B
C
E
D
无公共点,做垂直,证半径
分析:由于题中没有半径和公共点,所以过0作OE⊥AC,证明OE是半径即可。
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:有公共点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无公共点,作垂直,证半径。
O
B
A
C
O
A
B
C
E
D
归纳:
课堂练习:
1.如图1,已知直线EF经过⊙O上的点E,且OE=EF,若∠EOF=45°,则直线EF和⊙O的位置关系是
2.如图2,△ABC的一边AB是⊙O的直径,请你添加一个条件,是BC是⊙O的切线,你添加的条件是
E
F
O
相切
图1
∠ABC=90°
C
A
B
O
图2
巩固1:
如图,△ABC,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O
求证:AB是⊙O的切线
A
B
C
E
F
O
无公共点,做垂直,证半径
如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
求证:PE是⊙O的切线。
巩固2:
O
B
C
E
P
有公共点,连半径,证垂直
A
巩固3:
如图,△ABC中,∠ACB=90°,D是边AB上一点,且 ∠A=2∠DCB,E为边BC上一点,以EC为直径的⊙O经过点D.
求证:AB是⊙O的切线。
B
A
D
C
O
E
巩固4:
如图,AB是⊙O的直径,∠PAB=90°,连接PB交⊙O
于点C,D是PA边的中点,连接CD,
求证:CD是⊙O的切线。
A
O
B
D
C
P
小结
1.切线的判定
定义法:直线与圆有且只有一个公共点
数量法:直线到圆心的距离等于半径
切线的判定定理:过半径的外端且垂直这条半径的直线是圆的切线
2. 常用的添辅助线方法?
⑴有公共点,连半径,证垂直
⑵无公共点,作垂直,证半径
作业
教材:98页练习
101页3、4、5
再见!
人教版九年级上册
温故知新
1.直线和圆有哪些位置关系?
温故知新
直线与圆的位置关系
相交
相切
相离
公 共 点 个 数
公 共 点 名 称
直 线 名 称
图 形
圆心到直线距离d与半径r的关系
d
d>r
2
交点
割线
1
切点
切线
0
2.图中直线l满足什么条件时是⊙O的切线?你有几种方法判断?
O
方法一:直线与圆有且只有一个公共点
方法二:直线到圆心的距离等于半径
l
温故知新
A
O·
定义法:
数量法:
§24.2.2切线的判定定理
操作:
动手操作:
请在⊙O上任取一点A,连接OA,经过半径OA的外端点A作直线l⊥OA。
O
.
A
发现:
(1)直线l经过半径OA的
(2)直线l与半径OA
总结:直线l与⊙O的位置关系是
外端点A
垂直
相切
即直线l是⊙O的切线
O
.
A
切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两条: ①经过半径外端; ②垂直于这条半径
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
归纳:
判定直线与圆相切有哪些方法?
例题1
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连接OC(如图)。
∵ OA=OB
∴△AOC是等腰三角形
∵CA=CB
∴ OC是等腰三角形OAB底边AB上的中线
∴ AB⊥OC
∵ OC是⊙O的半径
∴ AB是⊙O的切线
有公共点,连半径,证垂直
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
例题2
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC OD⊥AB OE⊥AC
∴ OE=OD
∵ OD是⊙O的半径
∴OE是⊙O的半径
∴ AC是⊙O的切线。
O
A
B
C
E
D
无公共点,做垂直,证半径
分析:由于题中没有半径和公共点,所以过0作OE⊥AC,证明OE是半径即可。
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:有公共点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无公共点,作垂直,证半径。
O
B
A
C
O
A
B
C
E
D
归纳:
课堂练习:
1.如图1,已知直线EF经过⊙O上的点E,且OE=EF,若∠EOF=45°,则直线EF和⊙O的位置关系是
2.如图2,△ABC的一边AB是⊙O的直径,请你添加一个条件,是BC是⊙O的切线,你添加的条件是
E
F
O
相切
图1
∠ABC=90°
C
A
B
O
图2
巩固1:
如图,△ABC,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O
求证:AB是⊙O的切线
A
B
C
E
F
O
无公共点,做垂直,证半径
如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
求证:PE是⊙O的切线。
巩固2:
O
B
C
E
P
有公共点,连半径,证垂直
A
巩固3:
如图,△ABC中,∠ACB=90°,D是边AB上一点,且 ∠A=2∠DCB,E为边BC上一点,以EC为直径的⊙O经过点D.
求证:AB是⊙O的切线。
B
A
D
C
O
E
巩固4:
如图,AB是⊙O的直径,∠PAB=90°,连接PB交⊙O
于点C,D是PA边的中点,连接CD,
求证:CD是⊙O的切线。
A
O
B
D
C
P
小结
1.切线的判定
定义法:直线与圆有且只有一个公共点
数量法:直线到圆心的距离等于半径
切线的判定定理:过半径的外端且垂直这条半径的直线是圆的切线
2. 常用的添辅助线方法?
⑴有公共点,连半径,证垂直
⑵无公共点,作垂直,证半径
作业
教材:98页练习
101页3、4、5
再见!
同课章节目录
