苏科版九年级数学下册课件:6.5第2课时 相似三角形对应高、中线、角平分线的性质(共18张ppt)
文档属性
| 名称 | 苏科版九年级数学下册课件:6.5第2课时 相似三角形对应高、中线、角平分线的性质(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览



文档简介
第6章 图形的相似
6.5 第2课时 相似三角形对应高、中线、角平分线的性质
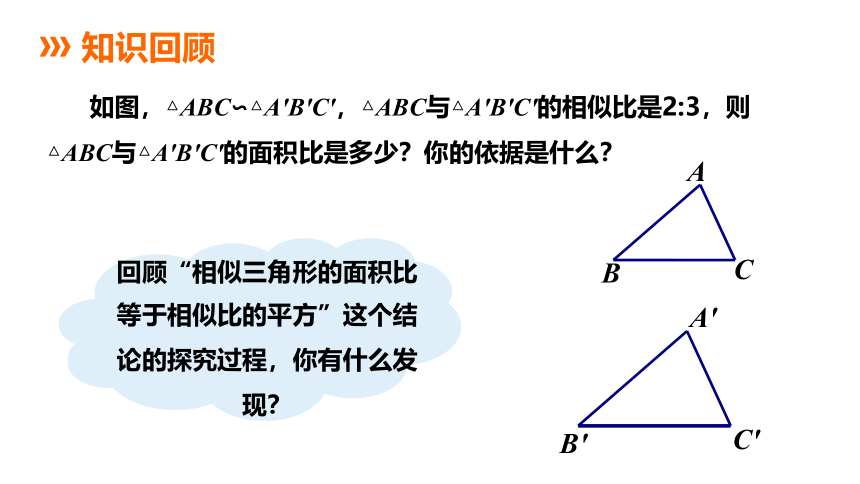
回顾“相似三角形的面积比
等于相似比的平方”这个结论的探究过程,你有什么发现?
A
B
C
C′
A′
B′
如图,△ABC∽△A'B'C',△ABC与△A'B'C'的相似比是2:3,则△ABC与△A'B'C'的面积比是多少?你的依据是什么?
知识回顾
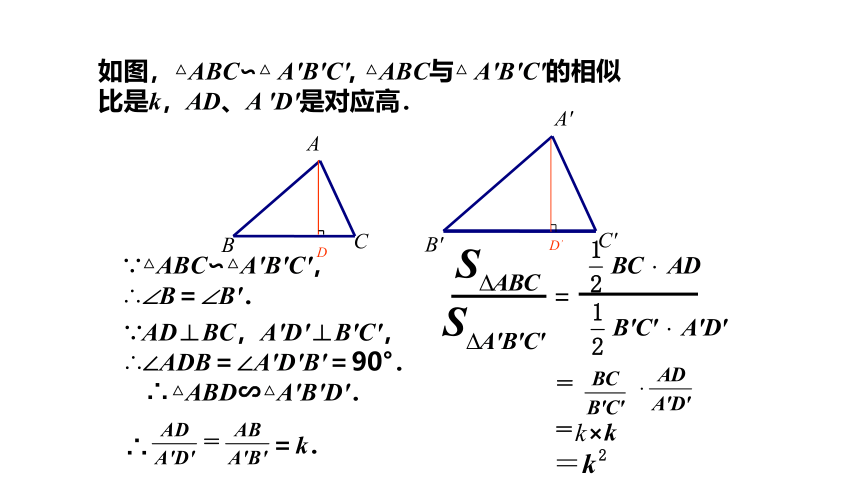
如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AD、A 'D'是对应高.
A
B
C
D
C′
A′
B′
D’
∵△ABC∽△A'B'C',
∴∠B=∠B'.
∵AD⊥BC,A'D'⊥B'C',
∴∠ADB=∠A'D'B'=90°.
∴△ABD∽△A'B'D'.
=k.
∴
k
×k
=
相似三角形对应高的比等于相似比.
三角形中的特殊线段还有哪些?它们是否也具有类似的性质呢?你有何猜想?
探究新知
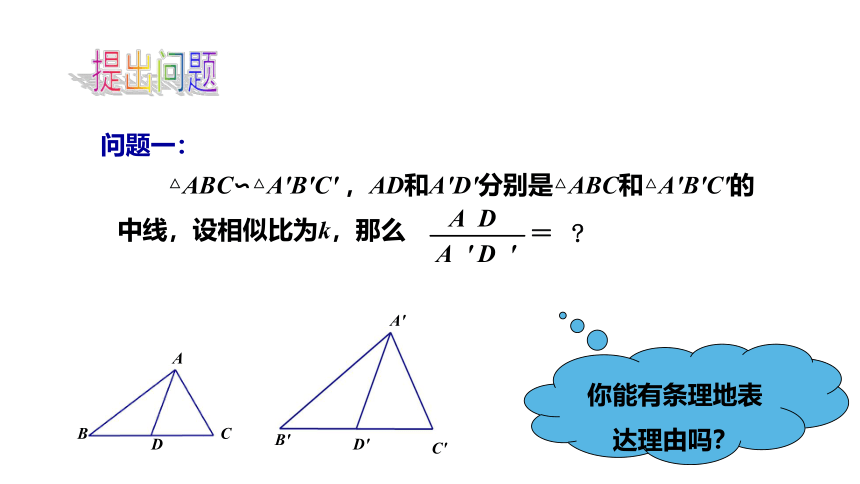
△ABC∽△A'B'C' ,AD和A'D'分别是△ABC和△A'B'C'的中线,设相似比为k,那么
你能有条理地表达理由吗?
C
A
B
D
C'
A'
D'
B'
问题一:
提出问题
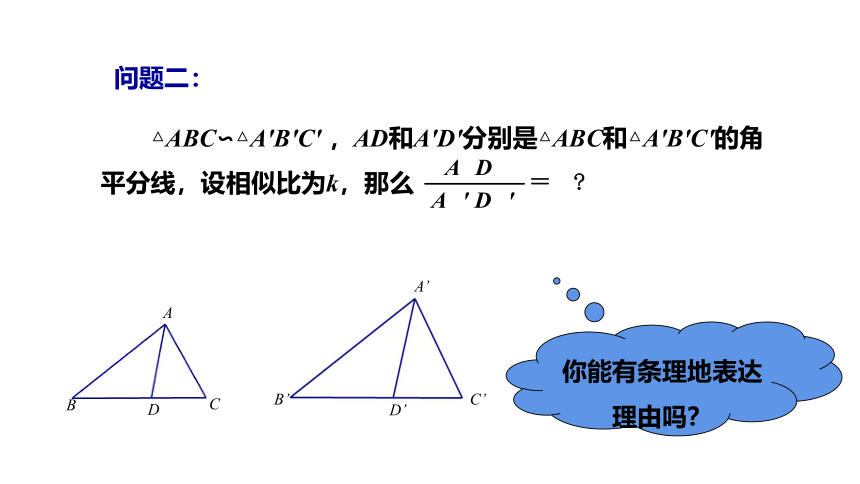
△ABC∽△A'B'C' ,AD和A'D'分别是△ABC和△A'B'C'的角平分线,设相似比为k,那么
A
B
D
C
C’
D’
B’
A’
你能有条理地表达理由吗?
问题二:
AD和A'D'分别是△ABC∽△A'B'C'的中线,
△ABC∽△ A'B'C',
∵
∴
,∠B=∠B'.
∵
∴
∴
∴
△ABD∽△A'B'D',
∴
∴
C
A
B
D
C'
A'
D'
B'
解决问题一
AD和A'D'分别是△ABC和△A'B'C'的角平分线,
△ABC∽△ A'B'C',
∵
∵
∴
∴
△ABD∽△A'B'D'.
∴
∴
∴∠BAC=∠B'A'C',∠B=∠B'.
解决问题二
A
B
D
C
C'
D'
B'
A'
归纳结论
相似三角形对应中线的比等于相似比.
相似三角形对应角平分线的比等于相似比.
一般地,如果△ABC∽△ A'B'C',相似比为k,点D、D'分别在BC、B'C'上,且 , 那么 .
相似三角形对应线段的比等于相似比.
C
A
B
D
C'
D'
B'
A'
你能类比刚才的方法说理吗?
例1 如图,AF是△ABC的高,点D、E分别在AB、AC上,DE ∥BC,DE交AF于点G .设DE=6,BC=10,GF=5,
求点A到DE、BC的距离.
例题讲解
ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
2.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=3cm ,则 ΔABC与ΔA1B1C1的对应高
之比为 .
8:3
随堂演练
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
相似三角形有哪些性质?
对应中线的比等于相似比
对应角平分线的比等于相似比
相
似
三
角
形
周长比等于相似比
面积比等于相似比的平方
相似三角形对应线段的比等于相似比.
课堂小结
谢谢观看!
6.5 第2课时 相似三角形对应高、中线、角平分线的性质
回顾“相似三角形的面积比
等于相似比的平方”这个结论的探究过程,你有什么发现?
A
B
C
C′
A′
B′
如图,△ABC∽△A'B'C',△ABC与△A'B'C'的相似比是2:3,则△ABC与△A'B'C'的面积比是多少?你的依据是什么?
知识回顾
如图,△ABC∽△ A'B'C', △ABC与△ A'B'C'的相似比是k,AD、A 'D'是对应高.
A
B
C
D
C′
A′
B′
D’
∵△ABC∽△A'B'C',
∴∠B=∠B'.
∵AD⊥BC,A'D'⊥B'C',
∴∠ADB=∠A'D'B'=90°.
∴△ABD∽△A'B'D'.
=k.
∴
k
×k
=
相似三角形对应高的比等于相似比.
三角形中的特殊线段还有哪些?它们是否也具有类似的性质呢?你有何猜想?
探究新知
△ABC∽△A'B'C' ,AD和A'D'分别是△ABC和△A'B'C'的中线,设相似比为k,那么
你能有条理地表达理由吗?
C
A
B
D
C'
A'
D'
B'
问题一:
提出问题
△ABC∽△A'B'C' ,AD和A'D'分别是△ABC和△A'B'C'的角平分线,设相似比为k,那么
A
B
D
C
C’
D’
B’
A’
你能有条理地表达理由吗?
问题二:
AD和A'D'分别是△ABC∽△A'B'C'的中线,
△ABC∽△ A'B'C',
∵
∴
,∠B=∠B'.
∵
∴
∴
∴
△ABD∽△A'B'D',
∴
∴
C
A
B
D
C'
A'
D'
B'
解决问题一
AD和A'D'分别是△ABC和△A'B'C'的角平分线,
△ABC∽△ A'B'C',
∵
∵
∴
∴
△ABD∽△A'B'D'.
∴
∴
∴∠BAC=∠B'A'C',∠B=∠B'.
解决问题二
A
B
D
C
C'
D'
B'
A'
归纳结论
相似三角形对应中线的比等于相似比.
相似三角形对应角平分线的比等于相似比.
一般地,如果△ABC∽△ A'B'C',相似比为k,点D、D'分别在BC、B'C'上,且 , 那么 .
相似三角形对应线段的比等于相似比.
C
A
B
D
C'
D'
B'
A'
你能类比刚才的方法说理吗?
例1 如图,AF是△ABC的高,点D、E分别在AB、AC上,DE ∥BC,DE交AF于点G .设DE=6,BC=10,GF=5,
求点A到DE、BC的距离.
例题讲解
ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
2.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=3cm ,则 ΔABC与ΔA1B1C1的对应高
之比为 .
8:3
随堂演练
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
相似三角形有哪些性质?
对应中线的比等于相似比
对应角平分线的比等于相似比
相
似
三
角
形
周长比等于相似比
面积比等于相似比的平方
相似三角形对应线段的比等于相似比.
课堂小结
谢谢观看!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
