苏科版数学八年级上册课件:6..2一次函数(共15张ppt)
文档属性
| 名称 | 苏科版数学八年级上册课件:6..2一次函数(共15张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 560.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 12:18:04 | ||
图片预览






文档简介
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
1.什么叫函数?
2.函数有哪些常见的表示方法?
图象法,表格法,代数表达式法(解析式法)
复习:(1分钟)
1.理解一次函数和正比例函数的概念,并会判断一个函数是否是一次函数,
2.能根据所给条件写出简单的一次函数表达式。
学习目标:(1分钟)
认真阅读课本P79中例1上面的的内容,完成下列问题:
1.回答P79的5个问题,特别是两个函数关系式的列法;
2.类比函数关系式:y=2x,y=0.7x-4,y=3(x+1)-5等,你可以发现这些函数关系式有什么共同特点?
3.若两个变量x ,y间的关系式可以表示成_________(k,b为_____且k_____)形式,则称y是x的一次函数(x为_______,y为_______)特别地,当b=___时,y=kx,称y是x的正比例函数。
y=0.5x+3
y=-0.18x+100
自学指导1:(7分钟)
K≠0,b可以为任意实数
y=kx+b
常数
自变量
因变量
0
≠0
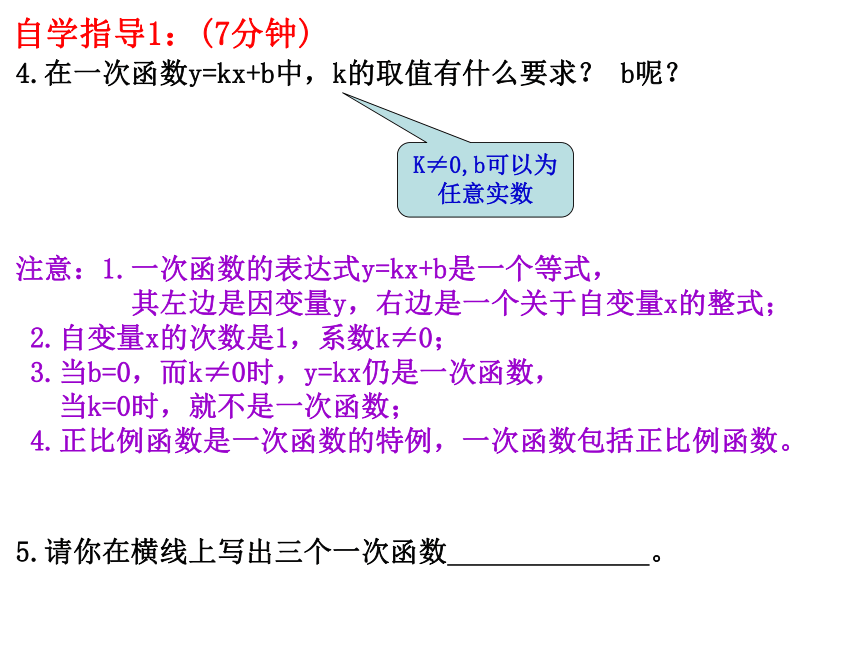
4.在一次函数y=kx+b中,k的取值有什么要求? b呢?
注意:1.一次函数的表达式y=kx+b是一个等式,
其左边是因变量y,右边是一个关于自变量x的整式;
2.自变量x的次数是1,系数k≠0;
3.当b=0,而k≠0时,y=kx仍是一次函数,
当k=0时,就不是一次函数;
4.正比例函数是一次函数的特例,一次函数包括正比例函数。
自学指导1:(7分钟)
5.请你在横线上写出三个一次函数 。
K≠0,b可以为任意实数
1.下列函数中,一次函数的是( )
A.y=8x2 B. y=x+1 C. y= D.y=
2.下列函数中,是一次函数但不是正比例函数的是( )
A.y= B.y= C.y= D.y=
3
x
1
X+2
B
C
3.练习册31页1,2,3题;
自学检测1:(7分钟)
4.一次函数y=-7x+3中,k= ,b= 。
-7
3
5.练习册32页选择题1,2,3题
C
B
A
认真阅读课本P79的例1,思考并完成:
1.根据自己对一次函数和正比例函数的理解,参照书中解答过程,回答下列问题:
①书中是根据什么列出的关系式?跟原来学过的 列方程是否一样?
②所列的函数解析式一般要化成什么形式?
③怎么样判断它是不是一次函数?
2.仿例题完成P80随堂练习-1T、2T,P82知识技能-1T。
自学指导2:(5分钟)
自学检测2(4分钟)
练习册32页解答题1。
认真阅读课本P80的例题2: 并思考:
1.在这个问题中,变量是什么?谁是自变量?谁是因变量?
2.答案(1)中“(x-3500)”是什么?
3.当知道自变量的值的时候,就能求出因变量的值,反之,当知道因变量的取值时是否也能求出自变量的取值?
自学指导3:(4分钟)
1.小明的月收入是1589元,他应缴所得税 元。
2.设月收入为x(元)且3500<x≤5000,则超过3500元的收入部分可表示为 ,超过部分的3﹪可表示为 。
3.仿例题完成课本P82问题解决-3T,4T ,5T。
x - 3500
3﹪( x -3500)
0
自学检测3:(8分钟)
P82问题解决:
3T解:(1)y=12+0.2x;
(2)当x=180时,y=12+0.2x=12+0.2×180=48元
∴当时间为180分时,他应缴费48元;
(3)当y=100时,100=12+0.2x即x=440
∴预交100元的话费,可通话440分钟。
4T解:(1)y=0.25x;
(2)当x=180时,y=0.25x=0.25×180=45元
∴当时间为180分时,他应缴费45元;
(3)当y=100时,100=0.25x即x=400
∴预交200元的话费,可通话400分钟。
P82问题解决:
5T解:(1)时间为300分时A类收费为12+0.2×300=72元;
B类收费为0.25×300=75元, 又75>72
∴若每月平均通话为300分,应选A类收费方式
(2)当12+0.2x=0.25x时, x=240
∴每月通话240分钟时,A、B两类收费相等。
小结:(1分钟)
1.一次函数:
若两个变量 x、y之间的关系可以表示成y=kx+b(k,b为常数,k不等于0)的形式,则称y是x的一次函数。(x为自变量,y为因变量)
当b=0时,称y是x的正比例函数
2.注意:
(1)一次函数的表达式y=kx+b是一个等式,其左边是因变量y,右边是一个关于自变量x的整式;
(2)自变量x的次数是1,系数k≠0,
(3)当b=0,而k≠0时,y=kx仍是一次函数,
当k=0时,就不是一次函数。
(4)正比例函数是一次函数的特例,一次函数包括正比例函数。
1.什么叫函数?
2.函数有哪些常见的表示方法?
图象法,表格法,代数表达式法(解析式法)
复习:(1分钟)
1.理解一次函数和正比例函数的概念,并会判断一个函数是否是一次函数,
2.能根据所给条件写出简单的一次函数表达式。
学习目标:(1分钟)
认真阅读课本P79中例1上面的的内容,完成下列问题:
1.回答P79的5个问题,特别是两个函数关系式的列法;
2.类比函数关系式:y=2x,y=0.7x-4,y=3(x+1)-5等,你可以发现这些函数关系式有什么共同特点?
3.若两个变量x ,y间的关系式可以表示成_________(k,b为_____且k_____)形式,则称y是x的一次函数(x为_______,y为_______)特别地,当b=___时,y=kx,称y是x的正比例函数。
y=0.5x+3
y=-0.18x+100
自学指导1:(7分钟)
K≠0,b可以为任意实数
y=kx+b
常数
自变量
因变量
0
≠0
4.在一次函数y=kx+b中,k的取值有什么要求? b呢?
注意:1.一次函数的表达式y=kx+b是一个等式,
其左边是因变量y,右边是一个关于自变量x的整式;
2.自变量x的次数是1,系数k≠0;
3.当b=0,而k≠0时,y=kx仍是一次函数,
当k=0时,就不是一次函数;
4.正比例函数是一次函数的特例,一次函数包括正比例函数。
自学指导1:(7分钟)
5.请你在横线上写出三个一次函数 。
K≠0,b可以为任意实数
1.下列函数中,一次函数的是( )
A.y=8x2 B. y=x+1 C. y= D.y=
2.下列函数中,是一次函数但不是正比例函数的是( )
A.y= B.y= C.y= D.y=
3
x
1
X+2
B
C
3.练习册31页1,2,3题;
自学检测1:(7分钟)
4.一次函数y=-7x+3中,k= ,b= 。
-7
3
5.练习册32页选择题1,2,3题
C
B
A
认真阅读课本P79的例1,思考并完成:
1.根据自己对一次函数和正比例函数的理解,参照书中解答过程,回答下列问题:
①书中是根据什么列出的关系式?跟原来学过的 列方程是否一样?
②所列的函数解析式一般要化成什么形式?
③怎么样判断它是不是一次函数?
2.仿例题完成P80随堂练习-1T、2T,P82知识技能-1T。
自学指导2:(5分钟)
自学检测2(4分钟)
练习册32页解答题1。
认真阅读课本P80的例题2: 并思考:
1.在这个问题中,变量是什么?谁是自变量?谁是因变量?
2.答案(1)中“(x-3500)”是什么?
3.当知道自变量的值的时候,就能求出因变量的值,反之,当知道因变量的取值时是否也能求出自变量的取值?
自学指导3:(4分钟)
1.小明的月收入是1589元,他应缴所得税 元。
2.设月收入为x(元)且3500<x≤5000,则超过3500元的收入部分可表示为 ,超过部分的3﹪可表示为 。
3.仿例题完成课本P82问题解决-3T,4T ,5T。
x - 3500
3﹪( x -3500)
0
自学检测3:(8分钟)
P82问题解决:
3T解:(1)y=12+0.2x;
(2)当x=180时,y=12+0.2x=12+0.2×180=48元
∴当时间为180分时,他应缴费48元;
(3)当y=100时,100=12+0.2x即x=440
∴预交100元的话费,可通话440分钟。
4T解:(1)y=0.25x;
(2)当x=180时,y=0.25x=0.25×180=45元
∴当时间为180分时,他应缴费45元;
(3)当y=100时,100=0.25x即x=400
∴预交200元的话费,可通话400分钟。
P82问题解决:
5T解:(1)时间为300分时A类收费为12+0.2×300=72元;
B类收费为0.25×300=75元, 又75>72
∴若每月平均通话为300分,应选A类收费方式
(2)当12+0.2x=0.25x时, x=240
∴每月通话240分钟时,A、B两类收费相等。
小结:(1分钟)
1.一次函数:
若两个变量 x、y之间的关系可以表示成y=kx+b(k,b为常数,k不等于0)的形式,则称y是x的一次函数。(x为自变量,y为因变量)
当b=0时,称y是x的正比例函数
2.注意:
(1)一次函数的表达式y=kx+b是一个等式,其左边是因变量y,右边是一个关于自变量x的整式;
(2)自变量x的次数是1,系数k≠0,
(3)当b=0,而k≠0时,y=kx仍是一次函数,
当k=0时,就不是一次函数。
(4)正比例函数是一次函数的特例,一次函数包括正比例函数。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
