湘教版(2012)初中数学八年级上册3.2 立方根 课件(共20张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册3.2 立方根 课件(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览




文档简介
3.2 立方根
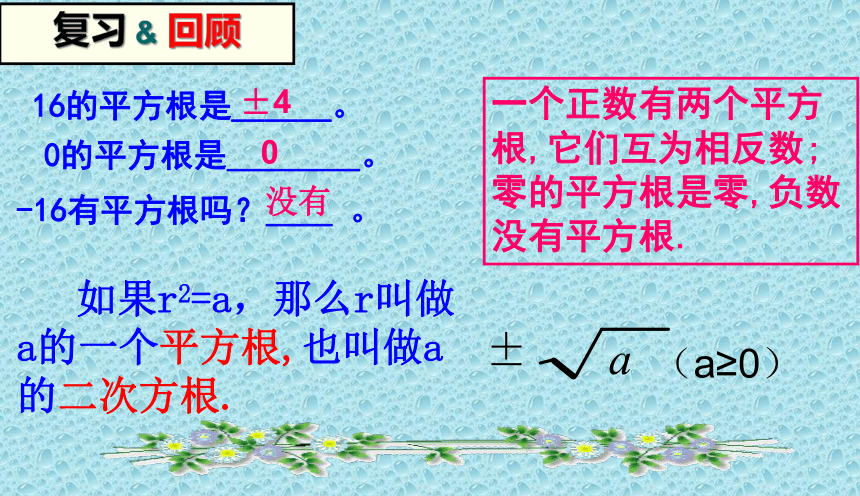
±
(a≥0)
如果r2=a,那么r叫做a的一个平方根,也叫做a的二次方根.
16的平方根是______。
-16有平方根吗?____ 。
0的平方根是________。
没有
0
一个正数有两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.
±4
复习 & 回顾
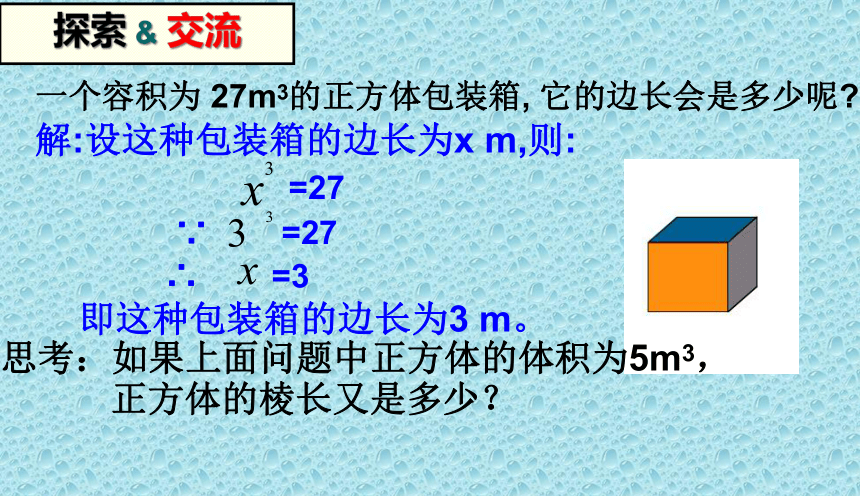
一个容积为 27m3的正方体包装箱, 它的边长会是多少呢?
解:设这种包装箱的边长为x m,则:
=27
∵ =27
∴ =3
即这种包装箱的边长为3 m。
探索 & 交流
思考:如果上面问题中正方体的体积为5m3,
正方体的棱长又是多少?
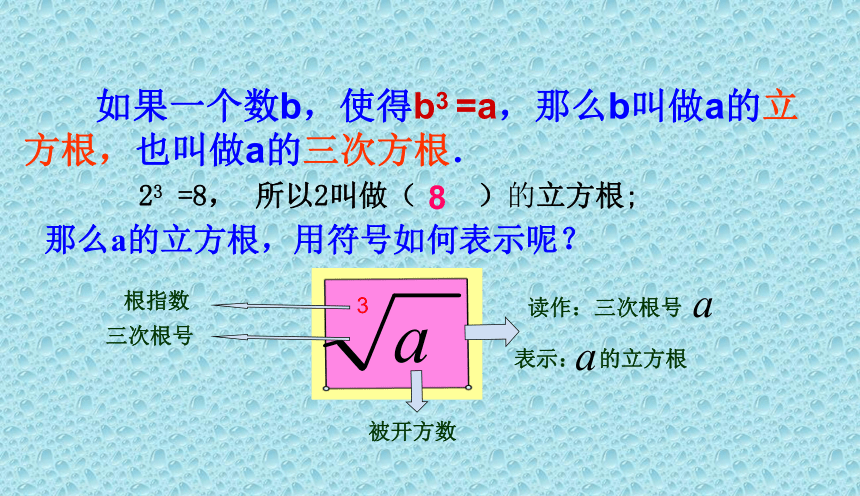
如果一个数b,使得b3 =a,那么b叫做a的立方根,也叫做a的三次方根.
8
23 =8,
所以2叫做( )的立方根;
那么a的立方根,用符号如何表示呢?
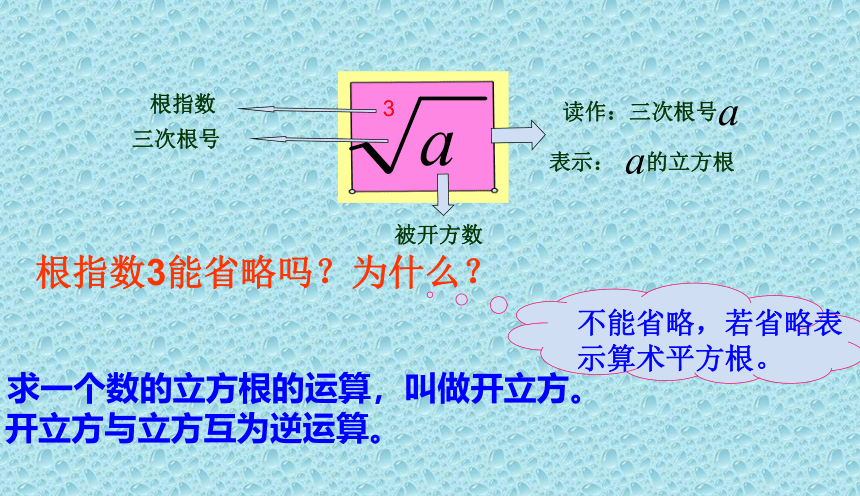
3
三次根号
根指数
被开方数
表示: 的立方根
读作:三次根号
根指数3能省略吗?为什么?
求一个数的立方根的运算,叫做开立方。
开立方与立方互为逆运算。
3
三次根号
根指数
被开方数
表示: 的立方根
读作:三次根号
不能省略,若省略表示算术平方根。
(1)27的立方根是多少?
(2)-27的立方根是多少?
(3)0的立方根是多少?
探索 & 交流
(1)正数的立方根是 数;
(2)负数的立方根是 数;
(3)0的立方根是 。
每一个数有且只有一个立方根
结论
立方根的性质
正
负
0
3
-3
0
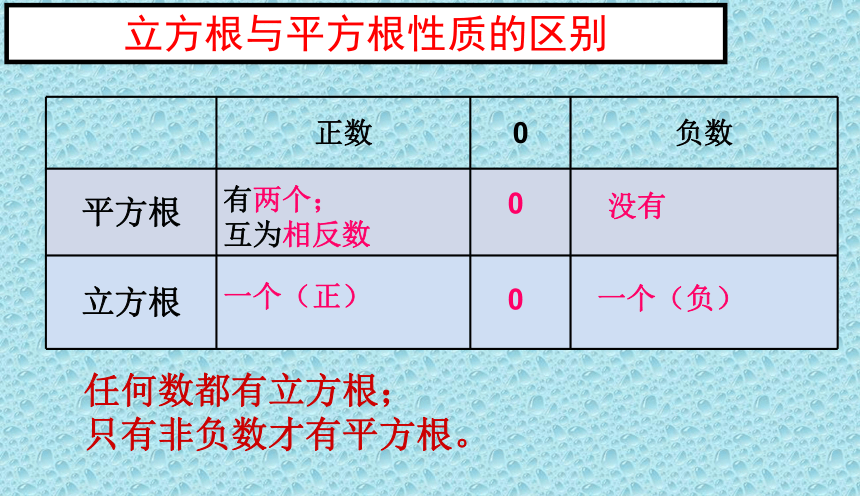
立方根与平方根性质的区别
正数
0
负数
平方根
立方根
任何数都有立方根;
只有非负数才有平方根。
有两个;
互为相反数
一个(正)
0
0
没有
一个(负)
1、5的立方根表示为( )
2、 ( )
3、下列说法正确的是( )
A.1的平方根是1 B.64的立方根是±4
C.-81没有立方根 D.任何数只有一个立方根
-2
D
例1、求下列各数的立方根。
(1)1 (2)- 0.064
(3)0 (4)
求下列各数的立方根
(1) 27 (2)-125
(3) (4)-0.008
例2、求下列各式中x的值。
(1)
(2)
通过这节课的学习,同学们有什么收获?
立方根定义,性质,及表示方法。
求一个数的立方根。
立方根和平方根的区别。
课堂小结:
填空
-2
-3
4.(-3)的立方根是
1. - 8的立方根是
,2的立方根是
3
5.
的立方根是
2. 1的平方根是____;立方根为____;
算术平方根为____ ;
3. 立方根是其本身的数是 ____.
±1
1
0,±1
1
的平方根是:
的立方根是:
±2
2
判断下列说法是否正确,并说明理由
x
√
1. 任何有理数都有立方根,它不是正数就是负数。
2. 0的平方根与立方根都是0。
3. 一个数的立方根有两个,它们互为相反数。
4. 若 ,则 。
x
√
计算:
1、填空
(1)
(2)由(1)猜测:
一个数a先开立方,然后再立方,最后的结果等于 ;
一个数b先立方,然后再求立方根,最后的结果等于 。
64
-64
-2
a
b
2
2、观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍。
反之也成立。
1
10
0.1
1000
10
1000
10
1.1
110
60
0.6
正方体的体积扩大为原来的8倍,则它的边长变为原来的
倍。
2
±
(a≥0)
如果r2=a,那么r叫做a的一个平方根,也叫做a的二次方根.
16的平方根是______。
-16有平方根吗?____ 。
0的平方根是________。
没有
0
一个正数有两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.
±4
复习 & 回顾
一个容积为 27m3的正方体包装箱, 它的边长会是多少呢?
解:设这种包装箱的边长为x m,则:
=27
∵ =27
∴ =3
即这种包装箱的边长为3 m。
探索 & 交流
思考:如果上面问题中正方体的体积为5m3,
正方体的棱长又是多少?
如果一个数b,使得b3 =a,那么b叫做a的立方根,也叫做a的三次方根.
8
23 =8,
所以2叫做( )的立方根;
那么a的立方根,用符号如何表示呢?
3
三次根号
根指数
被开方数
表示: 的立方根
读作:三次根号
根指数3能省略吗?为什么?
求一个数的立方根的运算,叫做开立方。
开立方与立方互为逆运算。
3
三次根号
根指数
被开方数
表示: 的立方根
读作:三次根号
不能省略,若省略表示算术平方根。
(1)27的立方根是多少?
(2)-27的立方根是多少?
(3)0的立方根是多少?
探索 & 交流
(1)正数的立方根是 数;
(2)负数的立方根是 数;
(3)0的立方根是 。
每一个数有且只有一个立方根
结论
立方根的性质
正
负
0
3
-3
0
立方根与平方根性质的区别
正数
0
负数
平方根
立方根
任何数都有立方根;
只有非负数才有平方根。
有两个;
互为相反数
一个(正)
0
0
没有
一个(负)
1、5的立方根表示为( )
2、 ( )
3、下列说法正确的是( )
A.1的平方根是1 B.64的立方根是±4
C.-81没有立方根 D.任何数只有一个立方根
-2
D
例1、求下列各数的立方根。
(1)1 (2)- 0.064
(3)0 (4)
求下列各数的立方根
(1) 27 (2)-125
(3) (4)-0.008
例2、求下列各式中x的值。
(1)
(2)
通过这节课的学习,同学们有什么收获?
立方根定义,性质,及表示方法。
求一个数的立方根。
立方根和平方根的区别。
课堂小结:
填空
-2
-3
4.(-3)的立方根是
1. - 8的立方根是
,2的立方根是
3
5.
的立方根是
2. 1的平方根是____;立方根为____;
算术平方根为____ ;
3. 立方根是其本身的数是 ____.
±1
1
0,±1
1
的平方根是:
的立方根是:
±2
2
判断下列说法是否正确,并说明理由
x
√
1. 任何有理数都有立方根,它不是正数就是负数。
2. 0的平方根与立方根都是0。
3. 一个数的立方根有两个,它们互为相反数。
4. 若 ,则 。
x
√
计算:
1、填空
(1)
(2)由(1)猜测:
一个数a先开立方,然后再立方,最后的结果等于 ;
一个数b先立方,然后再求立方根,最后的结果等于 。
64
-64
-2
a
b
2
2、观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍。
反之也成立。
1
10
0.1
1000
10
1000
10
1.1
110
60
0.6
正方体的体积扩大为原来的8倍,则它的边长变为原来的
倍。
2
同课章节目录
