鲁教版(五四制)九年级上学期 3.6二次函数有关长度、面积最值问题 专项练习(word版无答案)
文档属性
| 名称 | 鲁教版(五四制)九年级上学期 3.6二次函数有关长度、面积最值问题 专项练习(word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 185.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览

文档简介
如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4)
求二次函数的解析式和直线BD的解析式;
点P使直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
在抛物线上存在异于B、D的点Q,使△BDQ中BD边上的高为,请直接写出点Q的坐标。
2、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3)
(1)求这个二次函数的表达式并直接写出顶点坐标;
(2)若P是第一象限内这个二次函数图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC,设点P的横坐标为t.
①求线段PM的最大值;
②S△PBM:S△MHB=1:2时,求t的值;
③当△PCM时等腰三角形时,直接写出点P的坐标。
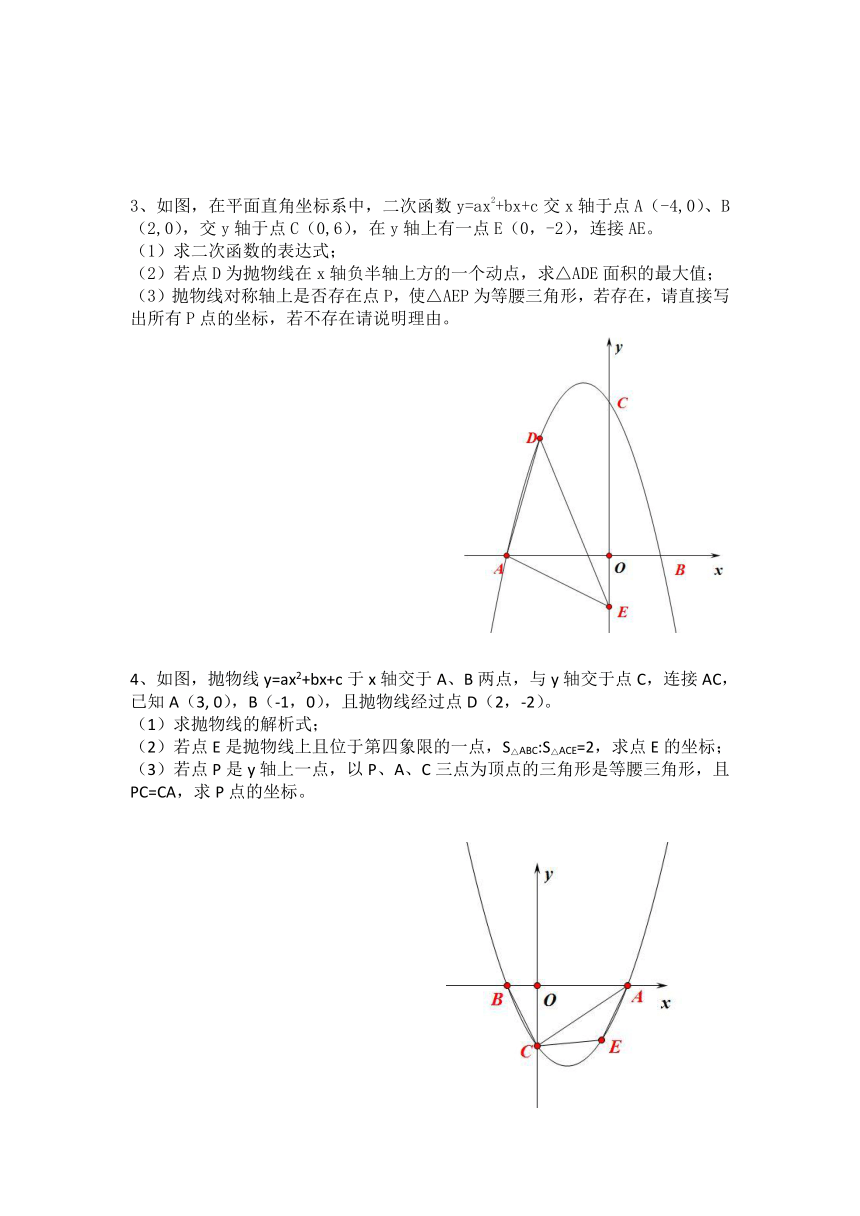
3、如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(-4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE。
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形,若存在,请直接写出所有P点的坐标,若不存在请说明理由。
4、如图,抛物线y=ax2+bx+c于x轴交于A、B两点,与y轴交于点C,连接AC,已知A(3,
0),B(-1,0),且抛物线经过点D(2,-2)。
(1)求抛物线的解析式;
(2)若点E是抛物线上且位于第四象限的一点,S△ABC:S△ACE=2,求点E的坐标;
(3)若点P是y轴上一点,以P、A、C三点为顶点的三角形是等腰三角形,且PC=CA,求P点的坐标。
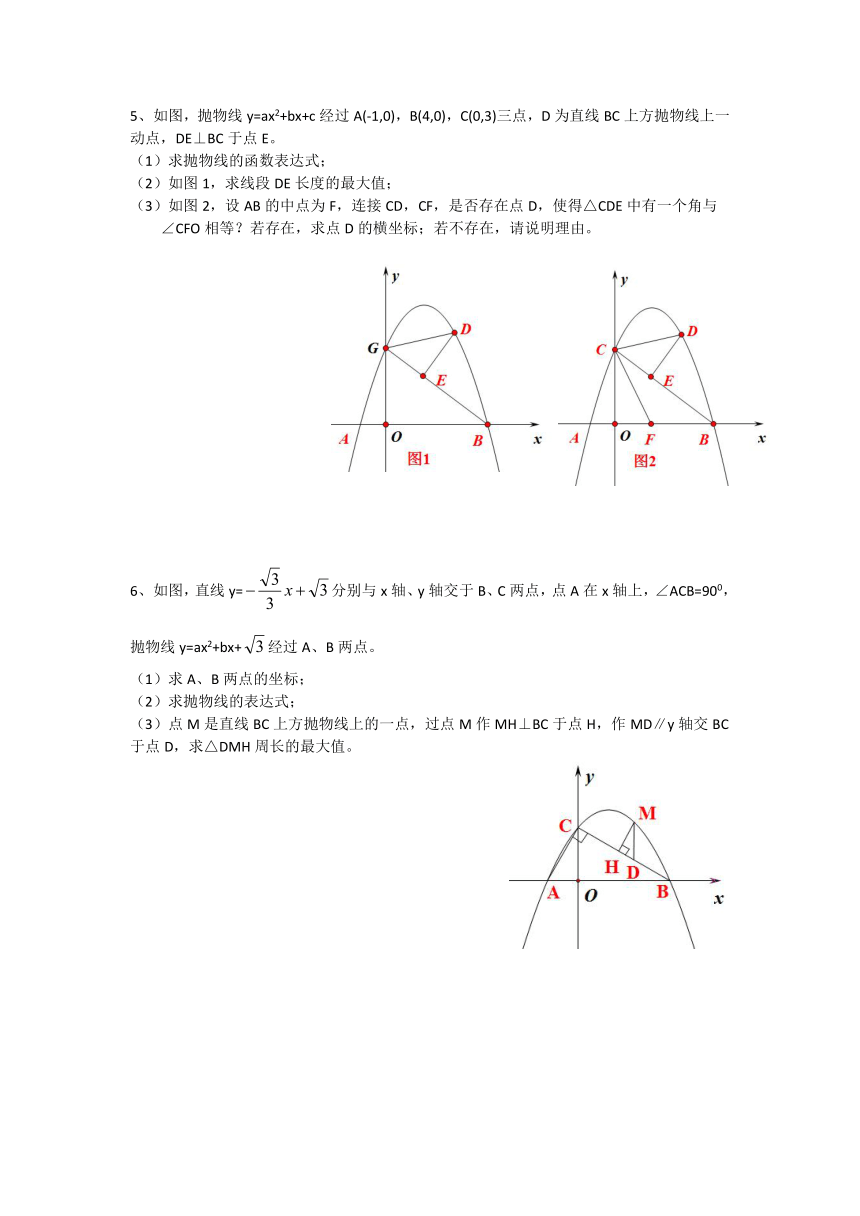
如图,抛物线y=ax2+bx+c经过A(-1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于点E。
求抛物线的函数表达式;
如图1,求线段DE长度的最大值;
如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与
∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由。
如图,直线y=分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=900,抛物线y=ax2+bx+经过A、B两点。
求A、B两点的坐标;
求抛物线的表达式;
点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值。
如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4。直线AD∥x轴,在x轴上有一动点E(t,0),过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P,Q。
求抛物线的表达式;
当0当t>2时,是否存在点P,使以A,P,Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由。
如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限内与直线y=x交于点B(2,t).
求这条抛物线的表达式;
在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB
?
若存在,求出点P的坐标;若不存在,请说明理由。
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(-2,1),交y轴于点M
求抛物线的函数表达式;
点D为抛物线在第二象限部分上的一点,作DE垂直于x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求出此时点D的坐标。
如图,已知抛物线y=ax2+bx+5经过A(-5,0),B(-4,-3)两点,与x轴的另一个交点为C,顶点为D,连接CD.
求抛物线的解析式及点C的坐标;
点P为该抛物线上一动点(与点B,C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求△PBC的面积的最大值;
②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由。
如图1,在平面直角坐标系xOy中,已知A(-2,2),B(-2,0),C(0,2),D(2,0)四点,动点M以每秒个单位长度的速度沿B——C——D运动(M不与点B、D重合),设运动时间为t(秒)
求经过A,C,D三点的抛物线的解析式;
点P在图1中的抛物线上,当M为BC的中点时,若△PAM
≌
△PBM,求点P的坐标;
当M在CD上运动时,如图2,过点M作MF⊥x轴,垂足为点F,ME⊥AB,垂足为点E.
设矩形MEBF与△BCD重叠部分的面积为S,求S与t的函数关系式,并求出S的最大值。
求二次函数的解析式和直线BD的解析式;
点P使直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
在抛物线上存在异于B、D的点Q,使△BDQ中BD边上的高为,请直接写出点Q的坐标。
2、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3)
(1)求这个二次函数的表达式并直接写出顶点坐标;
(2)若P是第一象限内这个二次函数图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC,设点P的横坐标为t.
①求线段PM的最大值;
②S△PBM:S△MHB=1:2时,求t的值;
③当△PCM时等腰三角形时,直接写出点P的坐标。
3、如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(-4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,-2),连接AE。
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形,若存在,请直接写出所有P点的坐标,若不存在请说明理由。
4、如图,抛物线y=ax2+bx+c于x轴交于A、B两点,与y轴交于点C,连接AC,已知A(3,
0),B(-1,0),且抛物线经过点D(2,-2)。
(1)求抛物线的解析式;
(2)若点E是抛物线上且位于第四象限的一点,S△ABC:S△ACE=2,求点E的坐标;
(3)若点P是y轴上一点,以P、A、C三点为顶点的三角形是等腰三角形,且PC=CA,求P点的坐标。
如图,抛物线y=ax2+bx+c经过A(-1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于点E。
求抛物线的函数表达式;
如图1,求线段DE长度的最大值;
如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与
∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由。
如图,直线y=分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=900,抛物线y=ax2+bx+经过A、B两点。
求A、B两点的坐标;
求抛物线的表达式;
点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值。
如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4。直线AD∥x轴,在x轴上有一动点E(t,0),过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P,Q。
求抛物线的表达式;
当0
如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限内与直线y=x交于点B(2,t).
求这条抛物线的表达式;
在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB
?
若存在,求出点P的坐标;若不存在,请说明理由。
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(-2,1),交y轴于点M
求抛物线的函数表达式;
点D为抛物线在第二象限部分上的一点,作DE垂直于x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求出此时点D的坐标。
如图,已知抛物线y=ax2+bx+5经过A(-5,0),B(-4,-3)两点,与x轴的另一个交点为C,顶点为D,连接CD.
求抛物线的解析式及点C的坐标;
点P为该抛物线上一动点(与点B,C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求△PBC的面积的最大值;
②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由。
如图1,在平面直角坐标系xOy中,已知A(-2,2),B(-2,0),C(0,2),D(2,0)四点,动点M以每秒个单位长度的速度沿B——C——D运动(M不与点B、D重合),设运动时间为t(秒)
求经过A,C,D三点的抛物线的解析式;
点P在图1中的抛物线上,当M为BC的中点时,若△PAM
≌
△PBM,求点P的坐标;
当M在CD上运动时,如图2,过点M作MF⊥x轴,垂足为点F,ME⊥AB,垂足为点E.
设矩形MEBF与△BCD重叠部分的面积为S,求S与t的函数关系式,并求出S的最大值。
