湘教版(2012)初中数学八年级上册4.4 一元一次不等式的应用 课件(共15张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册4.4 一元一次不等式的应用 课件(共15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 12:23:43 | ||
图片预览







文档简介
《数学》八年级上册
4.4 一元一次不等式的应用
1.用不等式表示:一辆轿车在公路上的行驶速度是akm/h,已知公路对轿车的限速是100km/h,那么可以表示为
一﹑创设情境,引入新课
a≤100
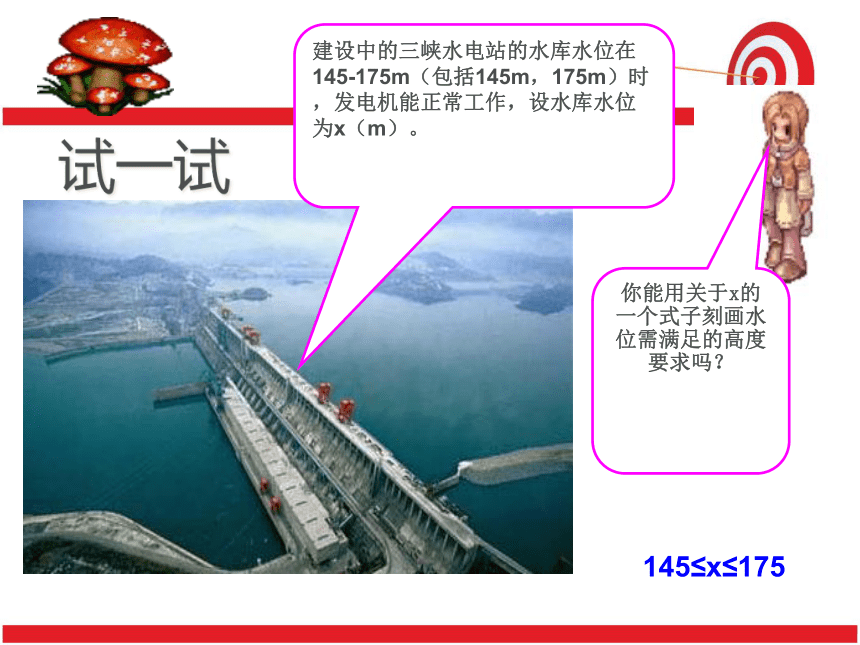
试一试
建设中的三峡水电站的水库水位在145-175m(包括145m,175m)时,发电机能正常工作,设水库水位为x(m)。
你能用关于x的一个式子刻画水位需满足的高度要求吗?
145≤x≤175
热身题:
根据题意列不等式:
1. a的5倍与7的和不大于0: ( )
2.同样一款毛衣,在A,B两店都有卖,A店标价68元,B店不只68元,用x表示B店这种毛衣的标价( )
3.甲有m元钱,乙有150元钱,甲的钱数不足乙的钱数的一半,则m满足的关系式是( )
4.某班有学生60人,学校规定参加运动会的人数至少是总人数的四分之一,若该班有x人参加,则x满足的关系式是( )。
5a+7≤0
x>68
m< ×150
x≥ 15
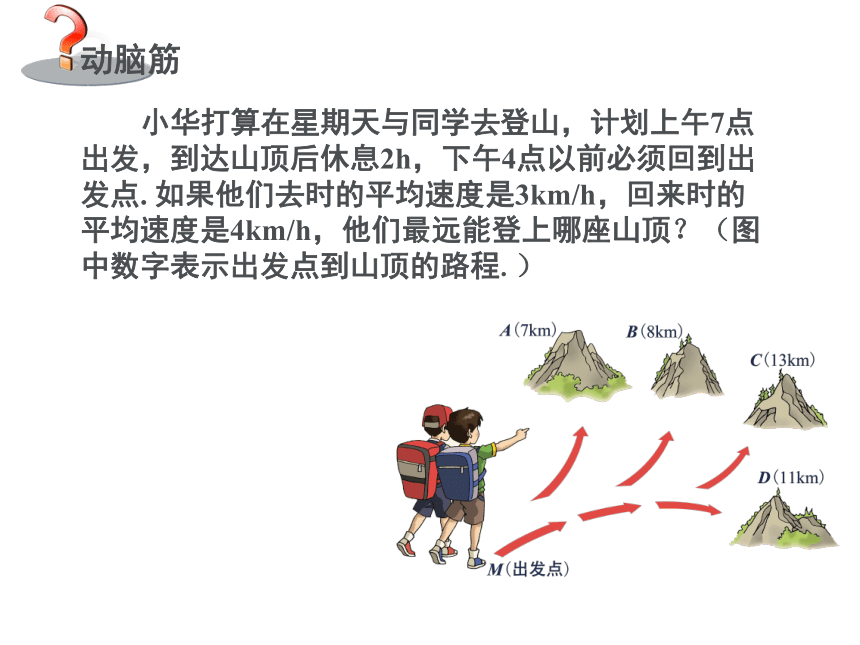
动脑筋
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶?(图中数字表示出发点到山顶的路程.)
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应少于或等于9 h.
所以有 +2+ ≤9.
解这个不等式,得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
二﹑师生合作,共探新知
探究(一):
1. 已知代数式 的值不小于代数式 +1的
值,试 确定x的最小整数值。
练习:若关于x的方程3x-m=3+x的解为非正数,求 m的取值范围 ?
举
例
例2
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
举
例
设每套童装的售价是x元.
解
则 40·x-90×40-40·x·10%≥900.
解这个不等式,得
x ≥ 125.
答:每套童装的售价至少是125元.
分析 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
探究(二):
应用一元一次不等式解决实际问题的步骤有哪些?
议一议
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
三﹑小组合作探究:
当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
设小明应搬动x本记事本,则
解
解这个不等式,得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
分析 本题涉及的数量关系是:
画册的总重+记事本的总重≤4.5 kg.
四﹑当堂检测,效果反馈
1. 小刚用100元钱去购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元,那么小刚最多能买钢笔( )
A.12 支 B.13 支 C.14 支 D.15支
2. 某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打( ) A.6 折 B.7 折 C. 8折 D.9折
3. 若x的6倍加上1小于x的3倍减去5,则x的取值范围是 ( )
4.某采石场爆破时,点燃导火线的甲工人要在爆破前转移到400米以外的安全区域。甲工人在转移过程中,前40米只能步行,之后骑自行车,已知导火线燃烧的速度为每秒0.01米 ,步行的速度为每秒1米,骑车的速度为每秒4米,为了确保甲工人的安全,则导火线的长度要大于 ( )
5.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解
设需要购买x块地板砖,则有
5×4≤x·0.6×0.6
解这个不等式,得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明至少要购买56块地板砖.
﹑
﹑
练习
6 . 某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解
设小琴最多打了x分钟的电话,则有
0.22+ (x-3) ×0.11<0.5
解这个不等式,得 x <5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5分钟的电话.
中考 链接
某学校要印刷一批宣传材料,甲印务公司提出收制版费900元,另外每份材料收印刷费0.5元;乙印务公司提出不收制版费,每份材料收印刷费0.8元.
(1)分别写出两家印务公司的收费y(元)与印刷材料的份数x(份)之间的函数关系式.
(2)若学校预计要印刷5000份以内的宣传材料,请问学校应选择哪一家印务公司更合算?
解
(1)y甲=900+0.5x,y乙=0.8x.
(2)令y甲>y乙,则900+0.5x>0.8x. 解之,得x<3000.
所以,当印刷3000份以内的宣传材料时选乙公司合算;
当印刷3000份以上5000份以内时,应选甲公司更合算.
五﹑课时小结,拓展升华;
1. 本课时学习了什么内容?有何收获?你还存在哪些方面的问题?如何改正?
2.某校组织师生春游,如果单独租用45座客车,刚好坐满,如果单独租用60座客车,可少租一辆,且余30个座位。(1)求该校参加春游的人数;(2)已知45座客车的租金为每辆250元,60座客车的租金为每辆300元,这次春游同时租用这两种客车,其中60座客车比45座客车多租一辆,所用租金比单独租用一种客车要节省,按照这种方案需租金多少元?
五﹑作业布置:
A组:1.篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队预计在2015~2016赛季全部32场比赛中最少得到48分,才有希望进入季后赛,假设这个对在将要举行的比赛中胜x场,要达到目标,x应满足的关系式是( )
A 2x+(32-x)≥48 B 2x-(32-x)≥48 C 2x+(32-x)≤48 D 2x≥48
2. 某出租车收费标准是起步价6元(3公里内6元),超过3千米后,每增加1千米加收1.4元(不足1千米按1千米计),某人乘这种出租车从甲地到乙地共付车费17.2元,设此人从甲地到乙地经过的路程为x千米,则x的最大值是( )
A 13 B 11 C 9 D 7
3.现用甲,乙两种运输车将56吨救灾物资运往灾区,甲种车载重为6吨,乙种运输车载重为5吨,案排车辆不超过10辆,则甲种运输车至少安排( ) A。4辆 B。5辆 C。6辆 D。7辆
填空题:
4.小刚在开学后,第一次测试数学得了70分,语文得了84分,则英语至少得 ( )分,才能使三科平均分不低于80分。
5.一个长方形的长为x米,宽为50米,如果它的周长不小于280米,那么 x应满足的不等式为 ( )。
6.一位老师说,她班学生的一半在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足6名学生在操场上踢足球,则这个班的学生最多有 ( )人。
B组 7. 某次个人象棋赛规定,赢1局得2分,平局得0分,负1局得 -1分。在12局比赛中,积分超过15分,就可晋升到下一轮比赛。王明进了下一轮比赛,而且在全部12局比赛中,没有出现平局,问王明可能输了几局比赛?
8. 宾馆里有一座电梯的最大载量为1000千克。两名宾馆服务员要用电梯把一批重物从底层搬到顶层,这两名服务员的身体质量分别为60千克和80千克,货物每箱的质量为50千克,问他们每次最多只能搬运重物多少箱?
建议讨论以下问题:
(1)选择哪一种数学模型?是列方程,还是列不等式?
(2)问题中有哪些相等的数量关系和不等的数量关系?
解:设他们每次能搬运重物X箱,根据题意得:
60+80+50X≤1000
解得 X≤17.2
答:他们每次最多能搬运重物17箱。
C组: 有一家庭工厂投资2万元购进一台机器,生产某种商品。这种商品每个的成本是3元,出售价是5元,应付的税款和其他费用是销售收入的10%。问至少需要生产、销售多少个这种商品,才能使所获利润(毛利润减去税款和其他费用)超过投资购买机器的费用?
(1)先从所求出发考虑问题,至少需要生产、销售多少个商品,使所获利润>购买机器款?
分析
(2)每生产、销售一个这样商品的利润是多少元?
生产、销售x个这样的商品的利润是多少元?这样
我们只要设生产、销售这种商品x个就可以了。
六﹑教学(学习)反思:
4.4 一元一次不等式的应用
1.用不等式表示:一辆轿车在公路上的行驶速度是akm/h,已知公路对轿车的限速是100km/h,那么可以表示为
一﹑创设情境,引入新课
a≤100
试一试
建设中的三峡水电站的水库水位在145-175m(包括145m,175m)时,发电机能正常工作,设水库水位为x(m)。
你能用关于x的一个式子刻画水位需满足的高度要求吗?
145≤x≤175
热身题:
根据题意列不等式:
1. a的5倍与7的和不大于0: ( )
2.同样一款毛衣,在A,B两店都有卖,A店标价68元,B店不只68元,用x表示B店这种毛衣的标价( )
3.甲有m元钱,乙有150元钱,甲的钱数不足乙的钱数的一半,则m满足的关系式是( )
4.某班有学生60人,学校规定参加运动会的人数至少是总人数的四分之一,若该班有x人参加,则x满足的关系式是( )。
5a+7≤0
x>68
m< ×150
x≥ 15
动脑筋
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶?(图中数字表示出发点到山顶的路程.)
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应少于或等于9 h.
所以有 +2+ ≤9.
解这个不等式,得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
二﹑师生合作,共探新知
探究(一):
1. 已知代数式 的值不小于代数式 +1的
值,试 确定x的最小整数值。
练习:若关于x的方程3x-m=3+x的解为非正数,求 m的取值范围 ?
举
例
例2
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
举
例
设每套童装的售价是x元.
解
则 40·x-90×40-40·x·10%≥900.
解这个不等式,得
x ≥ 125.
答:每套童装的售价至少是125元.
分析 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
探究(二):
应用一元一次不等式解决实际问题的步骤有哪些?
议一议
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
三﹑小组合作探究:
当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
设小明应搬动x本记事本,则
解
解这个不等式,得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
分析 本题涉及的数量关系是:
画册的总重+记事本的总重≤4.5 kg.
四﹑当堂检测,效果反馈
1. 小刚用100元钱去购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元,那么小刚最多能买钢笔( )
A.12 支 B.13 支 C.14 支 D.15支
2. 某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打( ) A.6 折 B.7 折 C. 8折 D.9折
3. 若x的6倍加上1小于x的3倍减去5,则x的取值范围是 ( )
4.某采石场爆破时,点燃导火线的甲工人要在爆破前转移到400米以外的安全区域。甲工人在转移过程中,前40米只能步行,之后骑自行车,已知导火线燃烧的速度为每秒0.01米 ,步行的速度为每秒1米,骑车的速度为每秒4米,为了确保甲工人的安全,则导火线的长度要大于 ( )
5.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解
设需要购买x块地板砖,则有
5×4≤x·0.6×0.6
解这个不等式,得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明至少要购买56块地板砖.
﹑
﹑
练习
6 . 某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解
设小琴最多打了x分钟的电话,则有
0.22+ (x-3) ×0.11<0.5
解这个不等式,得 x <5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5分钟的电话.
中考 链接
某学校要印刷一批宣传材料,甲印务公司提出收制版费900元,另外每份材料收印刷费0.5元;乙印务公司提出不收制版费,每份材料收印刷费0.8元.
(1)分别写出两家印务公司的收费y(元)与印刷材料的份数x(份)之间的函数关系式.
(2)若学校预计要印刷5000份以内的宣传材料,请问学校应选择哪一家印务公司更合算?
解
(1)y甲=900+0.5x,y乙=0.8x.
(2)令y甲>y乙,则900+0.5x>0.8x. 解之,得x<3000.
所以,当印刷3000份以内的宣传材料时选乙公司合算;
当印刷3000份以上5000份以内时,应选甲公司更合算.
五﹑课时小结,拓展升华;
1. 本课时学习了什么内容?有何收获?你还存在哪些方面的问题?如何改正?
2.某校组织师生春游,如果单独租用45座客车,刚好坐满,如果单独租用60座客车,可少租一辆,且余30个座位。(1)求该校参加春游的人数;(2)已知45座客车的租金为每辆250元,60座客车的租金为每辆300元,这次春游同时租用这两种客车,其中60座客车比45座客车多租一辆,所用租金比单独租用一种客车要节省,按照这种方案需租金多少元?
五﹑作业布置:
A组:1.篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分。某队预计在2015~2016赛季全部32场比赛中最少得到48分,才有希望进入季后赛,假设这个对在将要举行的比赛中胜x场,要达到目标,x应满足的关系式是( )
A 2x+(32-x)≥48 B 2x-(32-x)≥48 C 2x+(32-x)≤48 D 2x≥48
2. 某出租车收费标准是起步价6元(3公里内6元),超过3千米后,每增加1千米加收1.4元(不足1千米按1千米计),某人乘这种出租车从甲地到乙地共付车费17.2元,设此人从甲地到乙地经过的路程为x千米,则x的最大值是( )
A 13 B 11 C 9 D 7
3.现用甲,乙两种运输车将56吨救灾物资运往灾区,甲种车载重为6吨,乙种运输车载重为5吨,案排车辆不超过10辆,则甲种运输车至少安排( ) A。4辆 B。5辆 C。6辆 D。7辆
填空题:
4.小刚在开学后,第一次测试数学得了70分,语文得了84分,则英语至少得 ( )分,才能使三科平均分不低于80分。
5.一个长方形的长为x米,宽为50米,如果它的周长不小于280米,那么 x应满足的不等式为 ( )。
6.一位老师说,她班学生的一半在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足6名学生在操场上踢足球,则这个班的学生最多有 ( )人。
B组 7. 某次个人象棋赛规定,赢1局得2分,平局得0分,负1局得 -1分。在12局比赛中,积分超过15分,就可晋升到下一轮比赛。王明进了下一轮比赛,而且在全部12局比赛中,没有出现平局,问王明可能输了几局比赛?
8. 宾馆里有一座电梯的最大载量为1000千克。两名宾馆服务员要用电梯把一批重物从底层搬到顶层,这两名服务员的身体质量分别为60千克和80千克,货物每箱的质量为50千克,问他们每次最多只能搬运重物多少箱?
建议讨论以下问题:
(1)选择哪一种数学模型?是列方程,还是列不等式?
(2)问题中有哪些相等的数量关系和不等的数量关系?
解:设他们每次能搬运重物X箱,根据题意得:
60+80+50X≤1000
解得 X≤17.2
答:他们每次最多能搬运重物17箱。
C组: 有一家庭工厂投资2万元购进一台机器,生产某种商品。这种商品每个的成本是3元,出售价是5元,应付的税款和其他费用是销售收入的10%。问至少需要生产、销售多少个这种商品,才能使所获利润(毛利润减去税款和其他费用)超过投资购买机器的费用?
(1)先从所求出发考虑问题,至少需要生产、销售多少个商品,使所获利润>购买机器款?
分析
(2)每生产、销售一个这样商品的利润是多少元?
生产、销售x个这样的商品的利润是多少元?这样
我们只要设生产、销售这种商品x个就可以了。
六﹑教学(学习)反思:
同课章节目录
