湘教版数学八年级上册课件:2.5全等三角形的判定(AAS)(共15张ppt)
文档属性
| 名称 | 湘教版数学八年级上册课件:2.5全等三角形的判定(AAS)(共15张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 722.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 12:30:19 | ||
图片预览





文档简介
学习目标:
1.探索三角形的判定定理“角角边”定理
2.会用“角角边定理”和全等三角形的性质综合应用进行推理论证
知识回顾:
我们学习了几条判定三角形全等的定理?分别是那几条?
自主探究:
阅读课本第78至79页内容,并自主探究下列几个问题:
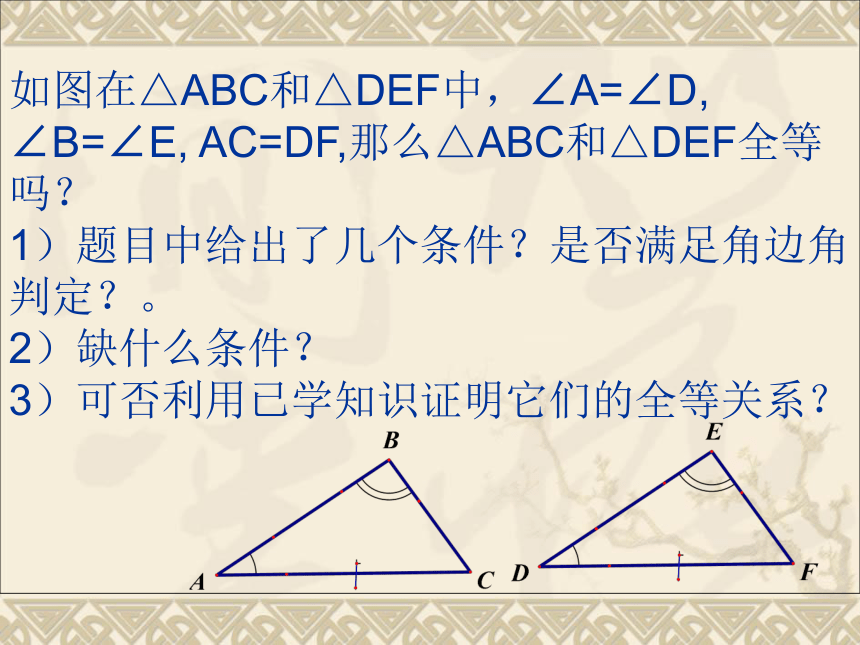
1.如图在△ABC和△DEF中,∠A=∠D, ∠B=∠E, AC=DF,那么△ABC和△DEF全等吗?
如图在△ABC和△DEF中,∠A=∠D, ∠B=∠E, AC=DF,那么△ABC和△DEF全等吗?
1)题目中给出了几个条件?是否满足角边角判定?。
2)缺什么条件?
3)可否利用已学知识证明它们的全等关系?
证明:
∵ ∠A=∠D,∠B=∠E
∴ -( ∠A + ∠B )= -( ∠D + ∠E )
即∠C=∠F
在△ABC和△DEF中
∵ ∠A=∠D
∠C=∠F
AC=DF
∴ △ABC≌ △DEF
(ASA)
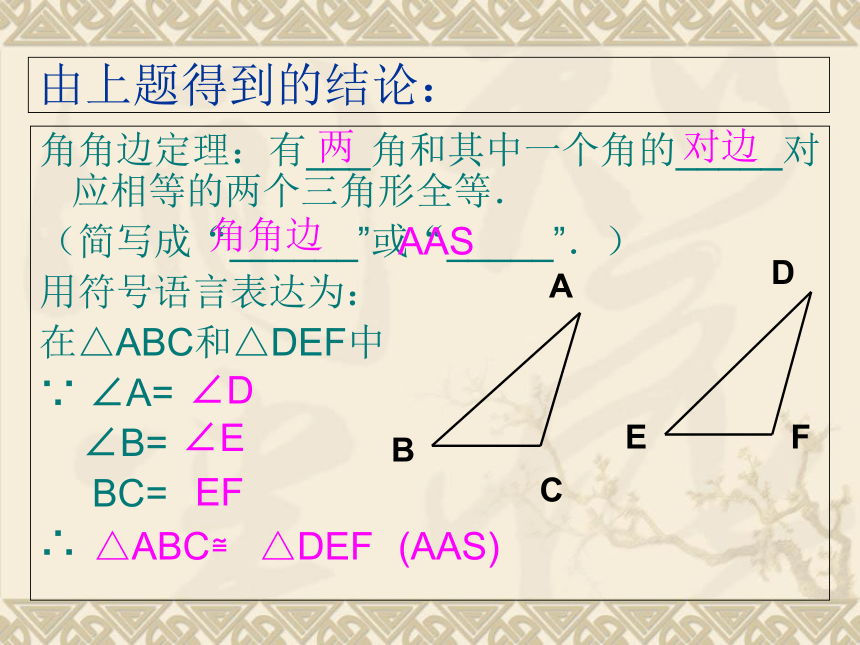
由上题得到的结论:
角角边定理:有___角和其中一个角的_____对应相等的两个三角形全等.
(简写成“______”或“_____”.)
用符号语言表达为:
在△ABC和△DEF中
∵ ∠A=
∠B=
BC=
∴
A
B
C
D
E
F
两
对边
角角边
AAS
∠D
∠E
EF
△ABC≌ △DEF
(AAS)
2.已知,如图,∠A=∠D, ∠1=∠2, 那么△ABC≌△DBC吗?
证明:
在△ABC和△DBC中
∠A=∠D
∠1=∠2
BC=BC
∵
∴
△ABC≌△DBC
(AAS)
合作交流:
已知,如图,AH=CM, ∠B=∠ K, AB∥HK,
求证:△ABC≌△HKM
证明:
∵AH=CM
∴AH+HC=CM+HC
即AC=HM
又∵ AB∥HK
∴∠A=∠KHM
(两直线平行,同位角相等)
在△ABC和△HKM中
∵ ∠B=∠ K
∠A=∠KHM
AC=HM
∴ △ABC≌△HKM
(AAS)
能力提升:
已知,AC=DC, AR⊥DC, DN⊥AC, AR和DN相等吗?为什么?
证明:
∵ AR⊥DC, DN⊥AC
∴∠ARC=∠DNC=
在△ARC和△DNC中
∠C= ∠C
∵∠ARC=∠DNC
AC=DC
∴ △ARC≌ △DNC
(AAS)
∴AR=DN
(全等三角形的对应边相等)
学习小结:
我们今天学到了什么?你现在学了哪几条三角形全等判定的方法?
作业:
如图,∠B=∠ E, AB=DE,
求证: AC= DC
选做题
如图,已知,AE=AC,∠1=∠2=∠3.
求证:BC=DE.
A
B
D
C
E
O
1
2
3
证明:
∵ ∠1=∠2
∴ ∠1+∠DAC=∠2+ ∠DAC
即∠BAC=∠DAE
又∵∠ADC=∠1+∠B
∠ ADC=∠ADE+∠3,, ∠1=∠3
∴∠B=∠ADE
在△ABC和△ADE中
∵∠B=∠ADE
∠BAC=∠DAE
AE=AC
∴△ABC≌△ADE
(AAS)
∴ BC=DE
(全等三角形的对应边相等)
小结
本节课你学了哪些知识?
下课
1.探索三角形的判定定理“角角边”定理
2.会用“角角边定理”和全等三角形的性质综合应用进行推理论证
知识回顾:
我们学习了几条判定三角形全等的定理?分别是那几条?
自主探究:
阅读课本第78至79页内容,并自主探究下列几个问题:
1.如图在△ABC和△DEF中,∠A=∠D, ∠B=∠E, AC=DF,那么△ABC和△DEF全等吗?
如图在△ABC和△DEF中,∠A=∠D, ∠B=∠E, AC=DF,那么△ABC和△DEF全等吗?
1)题目中给出了几个条件?是否满足角边角判定?。
2)缺什么条件?
3)可否利用已学知识证明它们的全等关系?
证明:
∵ ∠A=∠D,∠B=∠E
∴ -( ∠A + ∠B )= -( ∠D + ∠E )
即∠C=∠F
在△ABC和△DEF中
∵ ∠A=∠D
∠C=∠F
AC=DF
∴ △ABC≌ △DEF
(ASA)
由上题得到的结论:
角角边定理:有___角和其中一个角的_____对应相等的两个三角形全等.
(简写成“______”或“_____”.)
用符号语言表达为:
在△ABC和△DEF中
∵ ∠A=
∠B=
BC=
∴
A
B
C
D
E
F
两
对边
角角边
AAS
∠D
∠E
EF
△ABC≌ △DEF
(AAS)
2.已知,如图,∠A=∠D, ∠1=∠2, 那么△ABC≌△DBC吗?
证明:
在△ABC和△DBC中
∠A=∠D
∠1=∠2
BC=BC
∵
∴
△ABC≌△DBC
(AAS)
合作交流:
已知,如图,AH=CM, ∠B=∠ K, AB∥HK,
求证:△ABC≌△HKM
证明:
∵AH=CM
∴AH+HC=CM+HC
即AC=HM
又∵ AB∥HK
∴∠A=∠KHM
(两直线平行,同位角相等)
在△ABC和△HKM中
∵ ∠B=∠ K
∠A=∠KHM
AC=HM
∴ △ABC≌△HKM
(AAS)
能力提升:
已知,AC=DC, AR⊥DC, DN⊥AC, AR和DN相等吗?为什么?
证明:
∵ AR⊥DC, DN⊥AC
∴∠ARC=∠DNC=
在△ARC和△DNC中
∠C= ∠C
∵∠ARC=∠DNC
AC=DC
∴ △ARC≌ △DNC
(AAS)
∴AR=DN
(全等三角形的对应边相等)
学习小结:
我们今天学到了什么?你现在学了哪几条三角形全等判定的方法?
作业:
如图,∠B=∠ E, AB=DE,
求证: AC= DC
选做题
如图,已知,AE=AC,∠1=∠2=∠3.
求证:BC=DE.
A
B
D
C
E
O
1
2
3
证明:
∵ ∠1=∠2
∴ ∠1+∠DAC=∠2+ ∠DAC
即∠BAC=∠DAE
又∵∠ADC=∠1+∠B
∠ ADC=∠ADE+∠3,, ∠1=∠3
∴∠B=∠ADE
在△ABC和△ADE中
∵∠B=∠ADE
∠BAC=∠DAE
AE=AC
∴△ABC≌△ADE
(AAS)
∴ BC=DE
(全等三角形的对应边相等)
小结
本节课你学了哪些知识?
下课
同课章节目录
