16.1轴对称-冀教版八年级数学上册课件(共28张ppt)
文档属性
| 名称 | 16.1轴对称-冀教版八年级数学上册课件(共28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览







文档简介
16.1 轴对称
第十六章 轴对称和中心对称
冀教版八上
学 习 目 标
冀教版八上
1.认识轴对称图形,能够识别简单的轴对称图形.
2.理解两个图形成轴对称的概念,能够运用轴对称的性质作图.
3.理解线段垂直平分线的意义和线段的轴对称性并用其作图.
创设情境,引入新课
古代的建筑师、设计师在设计建筑或物品时,喜欢运用轴对称的元素,请欣赏......
创设情境,引入新课
天安门城楼给我们以什么样的印象?
庄严
创设情境,引入新课
故宫的建筑布局给我们以什么样的印象?
磅礴、大气
创设情境,引入新课
不只是在古代,在现在的生活中,也存在着各种各样的轴对称图形......
轴对称图形有什么共同特征呢?我们一起来学习吧...
新课学习
a
m
一、轴对称图形与轴对称的概念
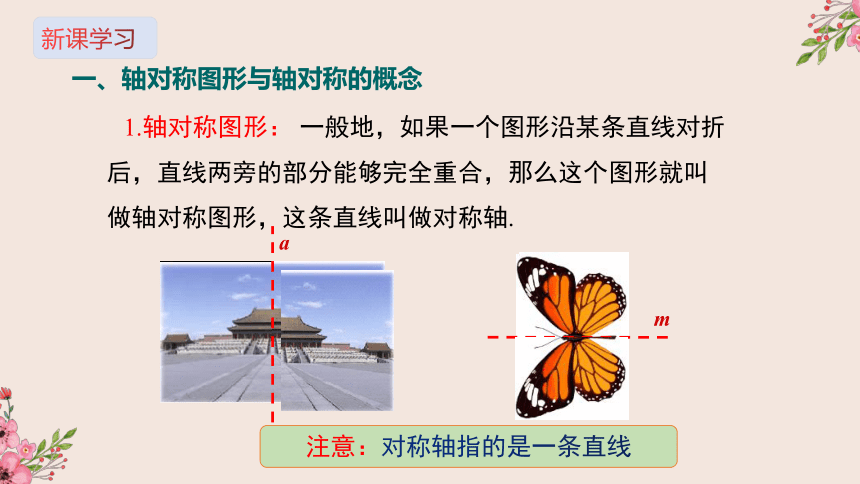
1.轴对称图形: 一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴.
注意:对称轴指的是一条直线
新课学习
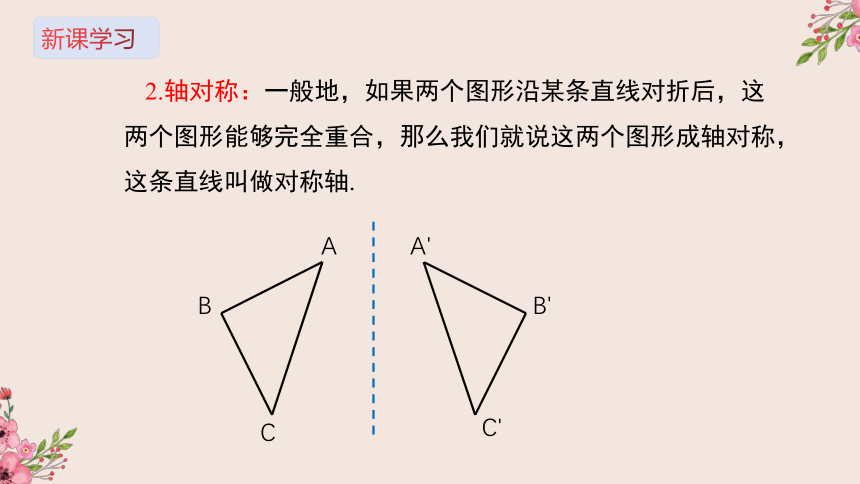
2.轴对称:一般地,如果两个图形沿某条直线对折后,这两个图形能够完全重合,那么我们就说这两个图形成轴对称,这条直线叫做对称轴.
A
C'
B'
A'
C
B
新课学习
3.轴对称图形与轴对称的区别与联系
如图,当我们把两扇门看做一个图形的时候,整个图形是一个轴对称图形,当我们把两扇门看做两个图形的时候,这两个扇门关于中间的一条线成轴对称.
新课学习
轴对称图形
两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
巩固练习
1.下列说法正确的是( ).
A.能够完全重合的两个图形成轴对称.
B.全等的两个图形成轴对称.
C.形状一样的两个图形成轴对称.
D.沿着一条直线对折能够重合的两个图形成轴对称.
D
巩固练习
2.如图,观察这几张图片,它们是不是轴对称图形?
√
√
×
判断方法:沿某直线对折看两旁是否重合.
新课学习
二、轴对称的性质
C
A'
A
B
B'
C'
l
如图,△ABC与△A'B'C'关于直线l是成轴对称.
注:关于对称轴对称的点、线段、角分别叫做对应点、对应线段、对应角.
新课学习
二、轴对称的性质
C
A'
A
B
B'
C'
l
(1)△ABC与△A'B'C'的关系是_______.
(2)对应线段的关系是______.
(3)对应角的关系是_______.
全等
相等
相等
新课学习
二、轴对称的性质
C
A'
A
B
B'
C'
l
(4)AA',BB',CC'之间的位置关系是_______.
(5)AA',BB',CC'与对称轴l的关系是___________________.
平行
被对称轴垂直平分
新课学习
二、轴对称的性质
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段平行,并且被对称轴垂直平分.
结论:
巩固练习
1.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN与点O,则下列说法不一定正确的是( ).
C
A'
A
B
B'
C'
O
N
M
A.AC=A'C' B.BO=B'O C.AA'⊥MN D.AB∥B'C'
D
巩固练习
2.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列说法错误的是( ).
A.AM=BM B.AP=BN C.∠MAP=∠MBP D.∠ANM=∠B
N
M
P
B
A
B
新课学习
1.定义:垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
三、线段的垂直平分线
线段是轴对称图形,线段的中垂线是它的对称轴.
新课学习
2.线段中垂线的用法
A
B
O
l
如图,直线l垂直平分AB,垂足为O.
①用于性质
∵直线l垂直平分AB.
∴OA=OB,l⊥AB.
②用于判定
∴直线l垂直平分AB.
∵OA=OB,l⊥AB.
典例精析
例题.已知线段AB和直线l,画出线段AB关于直线l的对称线段.
(3)用同样的方法画出点B的对称点B'
(2)延长AO到A',使A'O=AO.
解:(1)过点A画直线l的垂线段AO,垂足是O.
(4)连接线段A'B'.
线段A'B'即为所求.
所用知识点:
对应点所连的线段被对称轴垂直平分.
O
B
A
B'
A'
巩固总结
应用这种方法,只要给出对称轴,我们可以画任意多边形的对称图形.
对称轴的常见位置:
发现:对应线段所在的直线如果相交,交点一定在对称轴上.
课堂小测
1.在下列说法中,正确的是( ).
A.两个全等的三角形一定关于某条直线对称.
B.两个图形关于某条直线对称,对应点一定在直线两旁.
C.两个图形的对应点练习的垂线,就是它们的对称轴.
D.两个关于某直线对称的三角形是全等三角形.
D
课堂小测
2.如图,正方形ABCD的边长为5cm,则图中阴影部分的面积为__________.
12.5cm?
课堂小测
3.如图,在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,则符合条件的小正方形共有____个.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3
课堂小测
4.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C'处,折痕为EF,若AB=1,BC=2,则△ABE与△BC'F的周长之和为_______.
C
A
B
C'
D
E
F
6
课堂小结
轴对称
轴对称
轴对称图形
定义
性质
定义
性质
轴对称与
轴对称图形
联系
区别
同学们再见
第十六章 轴对称和中心对称
冀教版八上
学 习 目 标
冀教版八上
1.认识轴对称图形,能够识别简单的轴对称图形.
2.理解两个图形成轴对称的概念,能够运用轴对称的性质作图.
3.理解线段垂直平分线的意义和线段的轴对称性并用其作图.
创设情境,引入新课
古代的建筑师、设计师在设计建筑或物品时,喜欢运用轴对称的元素,请欣赏......
创设情境,引入新课
天安门城楼给我们以什么样的印象?
庄严
创设情境,引入新课
故宫的建筑布局给我们以什么样的印象?
磅礴、大气
创设情境,引入新课
不只是在古代,在现在的生活中,也存在着各种各样的轴对称图形......
轴对称图形有什么共同特征呢?我们一起来学习吧...
新课学习
a
m
一、轴对称图形与轴对称的概念
1.轴对称图形: 一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴.
注意:对称轴指的是一条直线
新课学习
2.轴对称:一般地,如果两个图形沿某条直线对折后,这两个图形能够完全重合,那么我们就说这两个图形成轴对称,这条直线叫做对称轴.
A
C'
B'
A'
C
B
新课学习
3.轴对称图形与轴对称的区别与联系
如图,当我们把两扇门看做一个图形的时候,整个图形是一个轴对称图形,当我们把两扇门看做两个图形的时候,这两个扇门关于中间的一条线成轴对称.
新课学习
轴对称图形
两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
巩固练习
1.下列说法正确的是( ).
A.能够完全重合的两个图形成轴对称.
B.全等的两个图形成轴对称.
C.形状一样的两个图形成轴对称.
D.沿着一条直线对折能够重合的两个图形成轴对称.
D
巩固练习
2.如图,观察这几张图片,它们是不是轴对称图形?
√
√
×
判断方法:沿某直线对折看两旁是否重合.
新课学习
二、轴对称的性质
C
A'
A
B
B'
C'
l
如图,△ABC与△A'B'C'关于直线l是成轴对称.
注:关于对称轴对称的点、线段、角分别叫做对应点、对应线段、对应角.
新课学习
二、轴对称的性质
C
A'
A
B
B'
C'
l
(1)△ABC与△A'B'C'的关系是_______.
(2)对应线段的关系是______.
(3)对应角的关系是_______.
全等
相等
相等
新课学习
二、轴对称的性质
C
A'
A
B
B'
C'
l
(4)AA',BB',CC'之间的位置关系是_______.
(5)AA',BB',CC'与对称轴l的关系是___________________.
平行
被对称轴垂直平分
新课学习
二、轴对称的性质
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段平行,并且被对称轴垂直平分.
结论:
巩固练习
1.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN与点O,则下列说法不一定正确的是( ).
C
A'
A
B
B'
C'
O
N
M
A.AC=A'C' B.BO=B'O C.AA'⊥MN D.AB∥B'C'
D
巩固练习
2.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列说法错误的是( ).
A.AM=BM B.AP=BN C.∠MAP=∠MBP D.∠ANM=∠B
N
M
P
B
A
B
新课学习
1.定义:垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
三、线段的垂直平分线
线段是轴对称图形,线段的中垂线是它的对称轴.
新课学习
2.线段中垂线的用法
A
B
O
l
如图,直线l垂直平分AB,垂足为O.
①用于性质
∵直线l垂直平分AB.
∴OA=OB,l⊥AB.
②用于判定
∴直线l垂直平分AB.
∵OA=OB,l⊥AB.
典例精析
例题.已知线段AB和直线l,画出线段AB关于直线l的对称线段.
(3)用同样的方法画出点B的对称点B'
(2)延长AO到A',使A'O=AO.
解:(1)过点A画直线l的垂线段AO,垂足是O.
(4)连接线段A'B'.
线段A'B'即为所求.
所用知识点:
对应点所连的线段被对称轴垂直平分.
O
B
A
B'
A'
巩固总结
应用这种方法,只要给出对称轴,我们可以画任意多边形的对称图形.
对称轴的常见位置:
发现:对应线段所在的直线如果相交,交点一定在对称轴上.
课堂小测
1.在下列说法中,正确的是( ).
A.两个全等的三角形一定关于某条直线对称.
B.两个图形关于某条直线对称,对应点一定在直线两旁.
C.两个图形的对应点练习的垂线,就是它们的对称轴.
D.两个关于某直线对称的三角形是全等三角形.
D
课堂小测
2.如图,正方形ABCD的边长为5cm,则图中阴影部分的面积为__________.
12.5cm?
课堂小测
3.如图,在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,则符合条件的小正方形共有____个.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3
课堂小测
4.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C'处,折痕为EF,若AB=1,BC=2,则△ABE与△BC'F的周长之和为_______.
C
A
B
C'
D
E
F
6
课堂小结
轴对称
轴对称
轴对称图形
定义
性质
定义
性质
轴对称与
轴对称图形
联系
区别
同学们再见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
