1 平行四边形的性质 第2课时(考点突破+题组训练+巩固练习)(含答案)
文档属性
| 名称 | 1 平行四边形的性质 第2课时(考点突破+题组训练+巩固练习)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 17:58:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
1 平行四边形的性质
第2课时
考点突破
考点1 平行四边形的对角线的性质
例1 (凉山州)如图, ABCD的对角线AC,BD交于点O,EF过点O且与BC,AD分别交于点E,F.试猜想线段AE,CF的关系,并说明理由。
思路导引: 根据平行四边形的性质得到OA=OC,AD∥BC,进而有∠AFE与∠CEF相等,再结合对顶角得出△AOF与△COE全等,得到OE与OF相等,再证明△AOE与△COF全等,从而得到AE与CF的关系。
方法归纳
1.本题利用全等知识也可以使结论获证,但相比而言,应用平行四边形对角线的性质求证更简洁明快因此,在学习了新知识后,要善于运用它,不受旧知识的限制与干扰,另辟蹊径,获取最佳解题方法。
2.平行四边形的性质是解决线段、角的有关问题的重要方法.过平行四边形对角线的交点的任意一条线平分平行四边形的面积。
题组训练
1.(泸州)如图, ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
第1题图 第2题图
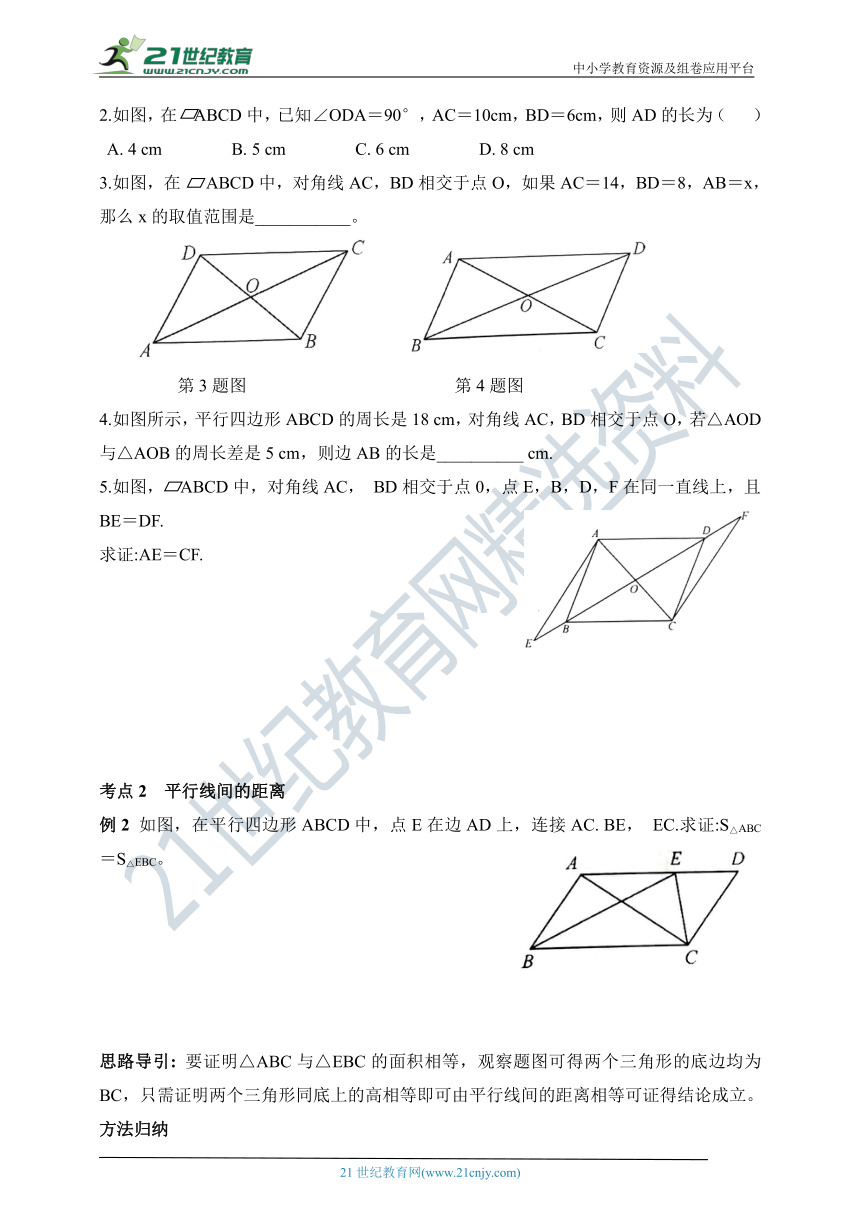
2.如图,在 ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A. 4 cm B. 5 cm C. 6 cm D. 8 cm
3.如图,在 ABCD中,对角线AC,BD相交于点O,如果AC=14,BD=8,AB=x,那么x的取值范围是___________。
第3题图 第4题图
4.如图所示,平行四边形ABCD的周长是18 cm,对角线AC,BD相交于点O,若△AOD与△AOB的周长差是5 cm,则边AB的长是__________ cm.
5.如图, ABCD中,对角线AC, BD相交于点0,点E,B,D,F在同一直线上,且BE=DF.
求证:AE=CF.
考点2 平行线间的距离
例2 如图,在平行四边形ABCD中,点E在边AD上,连接AC. BE, EC.求证:S△ABC=S△EBC。
思路导引: 要证明△ABC与△EBC的面积相等,观察题图可得两个三角形的底边均为BC,只需证明两个三角形同底上的高相等即可由平行线间的距离相等可证得结论成立。
方法归纳
点与点之间的距离是点到直线的距离、两条平行线之间的距离的基础,两条平行线之间的任何两条平行线段都相等,因为两条平行线与它们之间的平行线段构成平行四边形。
题组训练
6.如图所示,在平行四边形ABCD中,若∠A=45°,AD=,则AB与CD之间的距离为( )
A. B. C. D. 1
第6题图 第7题图
7.如图,AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于E,且OE=2,则AB与CD间的距离为_____________。
巩固练习
1. 平行四边形不一定具有的性质是( )
A.对角线互相平分 B.对角相等,邻角互补
C.对角线相等 D.对边平行且相等
2.(福州)平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B( 2,-1),C(-m,-n),则点D的坐标是( )
A.(-2,1) B. (-2,-1) C.(-1,-2) D. (-1,2)
3. 如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论正确的是 ( )
A. S平行四边形ABCD=4S△AOB B.AC=BD
C.AC⊥BD D.平行四边形ABCD是轴对称图形
第3题图 第4题图
4.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△OCD的周长为___________。
5.如图,已知直线a∥b,点C,D在直线a上,点A,B在直线b上,线段BC,AD相交于点E,写出图中所有面积相等的三角形:______________________________________
___________________________________________________________________。
第5题图 第6题图
(大连)如图,在平行四边形ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,
AC⊥BC,则OB=___________ cm.
7.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F.已知AB=4,BC=5,OE=1.
(1)求四边形EFCD的周长;
(2)若AB⊥AC,求四边形EFCD的面积。
8.如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形.请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由。
9.(广安)在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O.求证:OA=OE.
10.(宁波)如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…经过第2017次操作后得到的折痕D2016E2016到BC的距离记为h2017。若h1=1,则h2017的值为( )
A. B. C. 1- D. 2-
参考答案
考点突破
例1 解:AE∥CF且AE=CF.∵四边形ABCD为平行四边形,
∴OA=OC,AD∥BC∴∠AFE=∠CEF.
在△AOF和△COE中,∴△AOF≌△COE(AAS)∴OF=OE。
在△AOE和△COF中∴△AOE≌△COF(SAS).
∴AE=CF,∠OAE=∠OCF。∴AE∥CF.∴A∥CF且AE=CF.
题组训练
B 2. A 3. 3 < x < 11 4. 2
5.证明:(方法1)四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵BE=DF,∴OE=OF又∵∠AOE=∠COF,∴△AOE≌∠COF(SAS)∴AE=CF
(方法2)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠ABD=∠CDB.又∵∠ABE+∠ABD=180°,∠CDB+∠CDF=180°,∴∠ABE=∠CDF.在△ABE与△CDF中,AB=CD,∠ABE=∠CDF,BE=DF,∴△ABE≌△CDF(SAS).
∴AE=CF.
例2 证明:∵四边形ABCD是平行四边形,∴AD∥BC.作AM⊥BC于点C,EN⊥BC于点N(图略)∵AD∥BC,∴AM=EN.∵S△ABC=BC·AM,S△EBC=BC·EN,
∴S△ABC=S△EBC.
题组训练
6. B 7. 4
巩固练习
C 2. A 3. A 4. 21
△BAC与△ABD,△ACD与△BDC,△AEC与△BED
7.解:(1)∵四边形ABCD是平行四边形,∴OA=OC,CD=AB=4,AD∥BC.∴∠DAC=∠BCA.又∵∠AOE=∠COF,∴△AOE≌△COF.∴OE=OF,AE=CF.∴四边形EFCD的周长为EF+CF+CD+DE=2+AD+4=6+5=11.
(2)同理,可证△EOD≌△FOB,△COD≌△AOB.∴四边形EFCD的面积为四边形ABCD的面积一半.∵AB⊥AC,∴AC=√BC2-AB2=3∴ ABCD=AB·AC=12.∴四边形EFCD的面积为6.
8.解:连接AB,EF相交于点C,则射线OC就是所求的角平分线.
证明:∵四边形AEBF是平行四边形,∴AC=BC.∵OA=OB,∴OC平分∠AOB。
9.证明:(方法1)∵四边形ABCD为平行四边形,∴AD∥BC,且AD=BC∴∠ADB=∠CBD.由折叠可知∠EBD=∠CBD,BE=BC,∴∠EBD=∠ADB.∴BO=DO.∵AD=BE,∴AD-DO=BE-BO,即OA=OE.
(方法2)∵四边形ABCD为平行四边形,∴∠A=∠C,且AB=DC.由折叠可知∠E=∠C,DE=DC,∴∠A=∠E,AB=DE.又∵∠AOB=∠EOD,∴△AOB≌△EOD.
∴OA =OE.
D
_21?????????è?????(www.21cnjy.com)_
第五章 平行四边形
1 平行四边形的性质
第2课时
考点突破
考点1 平行四边形的对角线的性质
例1 (凉山州)如图, ABCD的对角线AC,BD交于点O,EF过点O且与BC,AD分别交于点E,F.试猜想线段AE,CF的关系,并说明理由。
思路导引: 根据平行四边形的性质得到OA=OC,AD∥BC,进而有∠AFE与∠CEF相等,再结合对顶角得出△AOF与△COE全等,得到OE与OF相等,再证明△AOE与△COF全等,从而得到AE与CF的关系。
方法归纳
1.本题利用全等知识也可以使结论获证,但相比而言,应用平行四边形对角线的性质求证更简洁明快因此,在学习了新知识后,要善于运用它,不受旧知识的限制与干扰,另辟蹊径,获取最佳解题方法。
2.平行四边形的性质是解决线段、角的有关问题的重要方法.过平行四边形对角线的交点的任意一条线平分平行四边形的面积。
题组训练
1.(泸州)如图, ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
第1题图 第2题图
2.如图,在 ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A. 4 cm B. 5 cm C. 6 cm D. 8 cm
3.如图,在 ABCD中,对角线AC,BD相交于点O,如果AC=14,BD=8,AB=x,那么x的取值范围是___________。
第3题图 第4题图
4.如图所示,平行四边形ABCD的周长是18 cm,对角线AC,BD相交于点O,若△AOD与△AOB的周长差是5 cm,则边AB的长是__________ cm.
5.如图, ABCD中,对角线AC, BD相交于点0,点E,B,D,F在同一直线上,且BE=DF.
求证:AE=CF.
考点2 平行线间的距离
例2 如图,在平行四边形ABCD中,点E在边AD上,连接AC. BE, EC.求证:S△ABC=S△EBC。
思路导引: 要证明△ABC与△EBC的面积相等,观察题图可得两个三角形的底边均为BC,只需证明两个三角形同底上的高相等即可由平行线间的距离相等可证得结论成立。
方法归纳
点与点之间的距离是点到直线的距离、两条平行线之间的距离的基础,两条平行线之间的任何两条平行线段都相等,因为两条平行线与它们之间的平行线段构成平行四边形。
题组训练
6.如图所示,在平行四边形ABCD中,若∠A=45°,AD=,则AB与CD之间的距离为( )
A. B. C. D. 1
第6题图 第7题图
7.如图,AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于E,且OE=2,则AB与CD间的距离为_____________。
巩固练习
1. 平行四边形不一定具有的性质是( )
A.对角线互相平分 B.对角相等,邻角互补
C.对角线相等 D.对边平行且相等
2.(福州)平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B( 2,-1),C(-m,-n),则点D的坐标是( )
A.(-2,1) B. (-2,-1) C.(-1,-2) D. (-1,2)
3. 如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论正确的是 ( )
A. S平行四边形ABCD=4S△AOB B.AC=BD
C.AC⊥BD D.平行四边形ABCD是轴对称图形
第3题图 第4题图
4.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△OCD的周长为___________。
5.如图,已知直线a∥b,点C,D在直线a上,点A,B在直线b上,线段BC,AD相交于点E,写出图中所有面积相等的三角形:______________________________________
___________________________________________________________________。
第5题图 第6题图
(大连)如图,在平行四边形ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,
AC⊥BC,则OB=___________ cm.
7.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F.已知AB=4,BC=5,OE=1.
(1)求四边形EFCD的周长;
(2)若AB⊥AC,求四边形EFCD的面积。
8.如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形.请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由。
9.(广安)在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O.求证:OA=OE.
10.(宁波)如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…经过第2017次操作后得到的折痕D2016E2016到BC的距离记为h2017。若h1=1,则h2017的值为( )
A. B. C. 1- D. 2-
参考答案
考点突破
例1 解:AE∥CF且AE=CF.∵四边形ABCD为平行四边形,
∴OA=OC,AD∥BC∴∠AFE=∠CEF.
在△AOF和△COE中,∴△AOF≌△COE(AAS)∴OF=OE。
在△AOE和△COF中∴△AOE≌△COF(SAS).
∴AE=CF,∠OAE=∠OCF。∴AE∥CF.∴A∥CF且AE=CF.
题组训练
B 2. A 3. 3 < x < 11 4. 2
5.证明:(方法1)四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵BE=DF,∴OE=OF又∵∠AOE=∠COF,∴△AOE≌∠COF(SAS)∴AE=CF
(方法2)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠ABD=∠CDB.又∵∠ABE+∠ABD=180°,∠CDB+∠CDF=180°,∴∠ABE=∠CDF.在△ABE与△CDF中,AB=CD,∠ABE=∠CDF,BE=DF,∴△ABE≌△CDF(SAS).
∴AE=CF.
例2 证明:∵四边形ABCD是平行四边形,∴AD∥BC.作AM⊥BC于点C,EN⊥BC于点N(图略)∵AD∥BC,∴AM=EN.∵S△ABC=BC·AM,S△EBC=BC·EN,
∴S△ABC=S△EBC.
题组训练
6. B 7. 4
巩固练习
C 2. A 3. A 4. 21
△BAC与△ABD,△ACD与△BDC,△AEC与△BED
7.解:(1)∵四边形ABCD是平行四边形,∴OA=OC,CD=AB=4,AD∥BC.∴∠DAC=∠BCA.又∵∠AOE=∠COF,∴△AOE≌△COF.∴OE=OF,AE=CF.∴四边形EFCD的周长为EF+CF+CD+DE=2+AD+4=6+5=11.
(2)同理,可证△EOD≌△FOB,△COD≌△AOB.∴四边形EFCD的面积为四边形ABCD的面积一半.∵AB⊥AC,∴AC=√BC2-AB2=3∴ ABCD=AB·AC=12.∴四边形EFCD的面积为6.
8.解:连接AB,EF相交于点C,则射线OC就是所求的角平分线.
证明:∵四边形AEBF是平行四边形,∴AC=BC.∵OA=OB,∴OC平分∠AOB。
9.证明:(方法1)∵四边形ABCD为平行四边形,∴AD∥BC,且AD=BC∴∠ADB=∠CBD.由折叠可知∠EBD=∠CBD,BE=BC,∴∠EBD=∠ADB.∴BO=DO.∵AD=BE,∴AD-DO=BE-BO,即OA=OE.
(方法2)∵四边形ABCD为平行四边形,∴∠A=∠C,且AB=DC.由折叠可知∠E=∠C,DE=DC,∴∠A=∠E,AB=DE.又∵∠AOB=∠EOD,∴△AOB≌△EOD.
∴OA =OE.
D
_21?????????è?????(www.21cnjy.com)_
