19.2.3 一次函数与方程、不等式(共16张ppt)
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 12:47:48 | ||
图片预览






文档简介
(共15张PPT)
19.2.3
一次函数与方程、不等式
人教版·八年级数学·下册
1.理解一次函数与一次方程、一次不等式的关系.
2.会用图象法解一元一次方程、不等式及方程组.
重点:理解函数与一次方程、一次不等式的关系.
难点:根据函数图象求一元一次方程的解和一次不等式的解集,发展学生数形结合的思想和辩证思维能力.
阅读课本第96-98页内容,学习本节主要内容.
小于0
大于0
x
横
0
方程、不等式与函数有着密切的联系.现在我们一起来探究一下怎样利用函数解方程和不等式.
1.(1)从“数”上看:求ax+b=0(a,b是常数,a≠0)的解,就是x为何值时,函数y=ax+b的值为_____;从“形”上看,求ax+b=0(a,b是常数,a≠0)的解,就是求直线y=ax+b与x轴交点的_______;
(2)解关于x的不等式kx+b>0或kx+b<0的转化思想:①kx+b>0可以转化为直线y=kx+b在x轴的_____方的点所对应的_____的取值;②kx+b<0可以转化为直线y=kx+b在x轴的_____方的点所对应的_____的值;
(3)解关于x、y的方程组
横坐标
0
上
相当于考虑当_____为何值时,两个函数的值相等以及这个_____为多少;从“形”的角度看,相当于确定两条直线y=kx+b与y=mx+n的交点.
y=kx+b
y=mx+n,
从“数”的角度看,
x
下
x
x
y
2.已知一次函数y=2x+6的图象如图所示,根据图象解答下列问题:
(1)求方程2x+6=0的解.
(2)求不等式2x+6>0,2x+6<0的解集.
(1)x=-3;
y
x
2
4
3
1
-2
-3
-1
-1
-2
4
5
6
0
1
2
3
y=2x+6
解:
(2)x>-3,x<-3.
观察图象,注意图象与x轴交点的横坐标.
教师点拨:
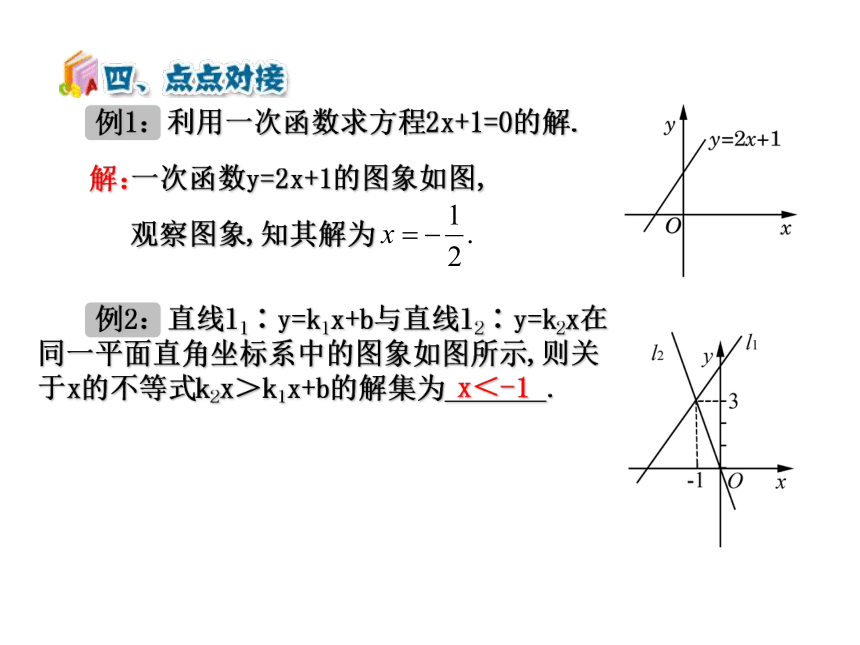
例1:利用一次函数求方程2x+1=0的解.
一次函数y=2x+1的图象如图,
解:
观察图象,知其解为
例2:直线l1∶y=k1x+b与直线l2∶y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为_______.
x<-1
例3:如图,直线l1经过点(2,2),直线l2经过点(0,5)、(1,3),求直线l1和l2交点A的坐标.
解:
设直线l1和l2的解析式分别为
y1=k1x(k1≠0),
y2=k2x+b(k2≠0),
由图象得:2k1=2,
根据条件确定两个一次函数解析式,然后解二元一次方程组,求得A点的坐标.
教师点拨:
k2+b=3,
b=5,
∴k1=1.
k2=-2
b=5,
∴l1的解析式为y=x,
l2的解析式为y=-2x+5.
∴点A的坐标为
1.如图所示,一次函数y=2x+m的图象过A、B两点,则方程2x+m=0的解是(
)
A.x=2
B.x=-1
C.x=0
D.无法确定
B
直接观察图象,找出与其x轴的交点横坐标即得到答案.
教师点拨:
2.已知关于x的不等式ax+1>0(a≠0)的解集是x<1,则直线y=ax+1与x轴的交点坐标是(
)
A.(0,1)
B.(1,0)
C.(0,-1)
D.(-1,0)
B
逆用图象法解不等式,即可求出点的坐标.
教师点拨:
3.求直线y=2x+4和y=-2x-2与y轴围成的三角形面积.
解:
设直线y=2x+4交y轴于点A(0,4),
∴
y=2x+4
y=-2x-2,
∴三角形的面积
交直线y=-2x-2于点B(x,y),
直线y=-2x-2交y轴于点C(0,-2),
求出两直线与y轴的交点坐标及两直线的交点坐标即可求三角形中相应线段及高的长,从而求得面积.
教师点拨:
x=1
C
(-5,0)
B
C
x
y
O
1
2
2
1
-1
-2
-1
-2
-3
解:
(3)由图象知,当x<0时,y>-1.
11.画出函数y=-2x-1的图象,并利用图象求:
(1)方程-2x-1=0的解;
(2)不等式-2x-1≥0的解集;
(3)当x<0时,y的取值范围;
(4)当y≤3时,x的取值范围.
1.列表:
2.描点、连线,如图所示:
x
0
1
y
-1
-3
y=-2x-1
(4)当y≤3时,
-2x-1
≤3
即:x≥-2.
1.利用函数直接得出方程、不等式及方程组的解.
2.数形结合思想的进一步体现及应用.
19.2.3
一次函数与方程、不等式
人教版·八年级数学·下册
1.理解一次函数与一次方程、一次不等式的关系.
2.会用图象法解一元一次方程、不等式及方程组.
重点:理解函数与一次方程、一次不等式的关系.
难点:根据函数图象求一元一次方程的解和一次不等式的解集,发展学生数形结合的思想和辩证思维能力.
阅读课本第96-98页内容,学习本节主要内容.
小于0
大于0
x
横
0
方程、不等式与函数有着密切的联系.现在我们一起来探究一下怎样利用函数解方程和不等式.
1.(1)从“数”上看:求ax+b=0(a,b是常数,a≠0)的解,就是x为何值时,函数y=ax+b的值为_____;从“形”上看,求ax+b=0(a,b是常数,a≠0)的解,就是求直线y=ax+b与x轴交点的_______;
(2)解关于x的不等式kx+b>0或kx+b<0的转化思想:①kx+b>0可以转化为直线y=kx+b在x轴的_____方的点所对应的_____的取值;②kx+b<0可以转化为直线y=kx+b在x轴的_____方的点所对应的_____的值;
(3)解关于x、y的方程组
横坐标
0
上
相当于考虑当_____为何值时,两个函数的值相等以及这个_____为多少;从“形”的角度看,相当于确定两条直线y=kx+b与y=mx+n的交点.
y=kx+b
y=mx+n,
从“数”的角度看,
x
下
x
x
y
2.已知一次函数y=2x+6的图象如图所示,根据图象解答下列问题:
(1)求方程2x+6=0的解.
(2)求不等式2x+6>0,2x+6<0的解集.
(1)x=-3;
y
x
2
4
3
1
-2
-3
-1
-1
-2
4
5
6
0
1
2
3
y=2x+6
解:
(2)x>-3,x<-3.
观察图象,注意图象与x轴交点的横坐标.
教师点拨:
例1:利用一次函数求方程2x+1=0的解.
一次函数y=2x+1的图象如图,
解:
观察图象,知其解为
例2:直线l1∶y=k1x+b与直线l2∶y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为_______.
x<-1
例3:如图,直线l1经过点(2,2),直线l2经过点(0,5)、(1,3),求直线l1和l2交点A的坐标.
解:
设直线l1和l2的解析式分别为
y1=k1x(k1≠0),
y2=k2x+b(k2≠0),
由图象得:2k1=2,
根据条件确定两个一次函数解析式,然后解二元一次方程组,求得A点的坐标.
教师点拨:
k2+b=3,
b=5,
∴k1=1.
k2=-2
b=5,
∴l1的解析式为y=x,
l2的解析式为y=-2x+5.
∴点A的坐标为
1.如图所示,一次函数y=2x+m的图象过A、B两点,则方程2x+m=0的解是(
)
A.x=2
B.x=-1
C.x=0
D.无法确定
B
直接观察图象,找出与其x轴的交点横坐标即得到答案.
教师点拨:
2.已知关于x的不等式ax+1>0(a≠0)的解集是x<1,则直线y=ax+1与x轴的交点坐标是(
)
A.(0,1)
B.(1,0)
C.(0,-1)
D.(-1,0)
B
逆用图象法解不等式,即可求出点的坐标.
教师点拨:
3.求直线y=2x+4和y=-2x-2与y轴围成的三角形面积.
解:
设直线y=2x+4交y轴于点A(0,4),
∴
y=2x+4
y=-2x-2,
∴三角形的面积
交直线y=-2x-2于点B(x,y),
直线y=-2x-2交y轴于点C(0,-2),
求出两直线与y轴的交点坐标及两直线的交点坐标即可求三角形中相应线段及高的长,从而求得面积.
教师点拨:
x=1
C
(-5,0)
B
C
x
y
O
1
2
2
1
-1
-2
-1
-2
-3
解:
(3)由图象知,当x<0时,y>-1.
11.画出函数y=-2x-1的图象,并利用图象求:
(1)方程-2x-1=0的解;
(2)不等式-2x-1≥0的解集;
(3)当x<0时,y的取值范围;
(4)当y≤3时,x的取值范围.
1.列表:
2.描点、连线,如图所示:
x
0
1
y
-1
-3
y=-2x-1
(4)当y≤3时,
-2x-1
≤3
即:x≥-2.
1.利用函数直接得出方程、不等式及方程组的解.
2.数形结合思想的进一步体现及应用.
