小学数学人教版五年级上6谁的面积最大教案
图片预览

文档简介
《谁的面积最大》项目化教学设计
学习目标
引导学生基于真实的情境任务——猪圈围成什么形状既能节省成本,又能围的面积最大呢?针对这一驱动性问题,展开讨论探究。使学生发现解决这一驱动性问题也就是解决“周长相等的平面图形,谁的面积最大?”这一问题。接下来,引导学生们借助已有的知识经验、生活经验经历从发现问题、分析问题、合作探究、解决问题的过程。在这一过程中融合各学科的知识,充分发挥小组合作的能力、动手操作能力,培养了学生们综合运用各学科知识与方法解决实际问题的能力。与此同时,培养了学生们的问题意识、应用意识和创新意识,为今后的学习积累活动经验,不断提高解决现实问题的能力。
驱动性问题
猪圈围成什么形状既能节省成本,又能围的面积最大呢?
学习任务设计与实施
学习任务设计:
这节课首先结合“由于当前猪肉等农产品大幅上涨,农场主想扩大自己的养殖规模。”这一真实情景,提出驱动性问题“猪圈围成什么形状既能节省成本,又能围的面积最大呢?”首先引导学生将驱动性问题转化成数学问题“周长相等的平面图形,谁的面积最大?”然后,引导学生们结合自己的各学科知识经验展开思考、讨论,并且小组合作选取材料、工具进行探究、操作,然后得出结论、汇报,最后进行评价。在整个的过程中,培养了学生们的问题意识、应用意识和创新意识,为今后的学习积累活动经验,不断提高解决现实问题的能力。
项目实施:
一. 情境导入,引出驱动性问题
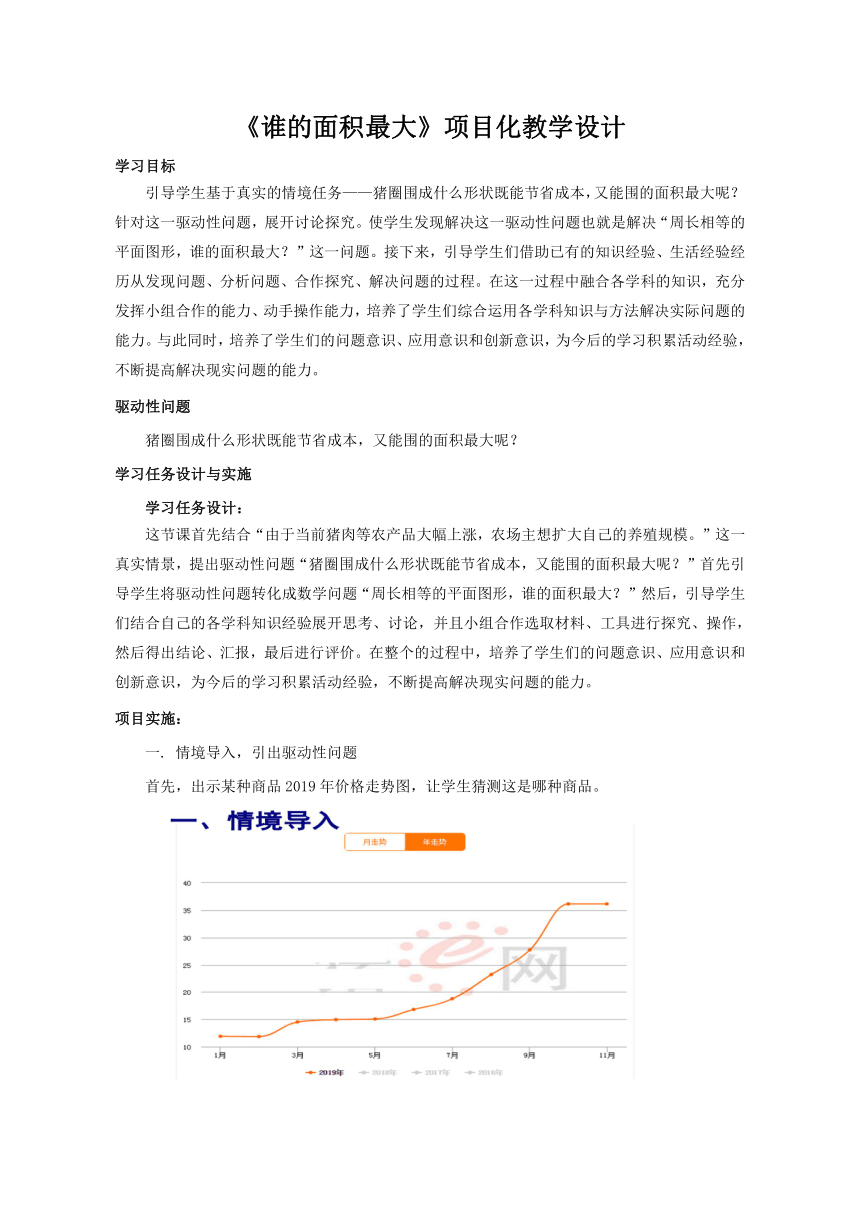
首先,出示某种商品2019年价格走势图,让学生猜测这是哪种商品。
引出答案,这是2019年猪肉价格的年走势图。
师:看到这个走势图,你有什么想法?学生各抒己见。
师:由于当前猪肉等农产品大幅上涨,农场主想扩大自己的养殖规模。所以就需要盖猪圈,猪圈围成什么形状既能节省成本,又能围的面积最大呢?
教师引导学生将这一问题转化成数学问题“周长相等的平面图形,谁的面积最大?”
二. 头脑风暴
在没有任何约束条件限制的情况下学生头脑风暴,提出了各种多样化的方法并及时探讨方法的可行性。有的同学会想到猪圈的材料选择、高度、围成的形状等问题。为了缩短项目的时间,教师加上条件限制,如果猪圈的高度和材料一定的情况下,我们怎么样满足农场主的要求。从而引导学生将农场主的问题转化成数学问题“周长相等的平面图形,谁的面积最大?”针对这样一个问题,有的同学认为,把图形的周长假设成一个固定的值,求出面积就可以,但是发现假设数据只能求出圆和正方形的面积。所以,最后统一思路,要想解决这个问题,必须通过在操作中实际测量数据求面积,也就是利用一根固定长度的铁丝,围成平面图形,然后计算平面图形面积,并对比各种图形面积的大小。
各小组继续讨论交流,并猜测围成哪一种平面图形面积最大。
教师课件学过求面积的图形。
(三角形、正方形、长方形、平行四边形、梯形、圆形。)
当猜测到圆的面积时,教师可以结合翻转课堂的小视频给学生们进行学习。
接下来各小组选择自己小组要验证的图形,进行操作。
师:如果要围成三角形,你认为围成什么三角形更有优势?
生:等边三角形!师:那就需要我们操作验证了。
师:那么,对于四边形我们是不是都要验证?
通过平行四边形扣条学具和课件演示,引导学生发现平行四边形和梯形都没有长方形有优势,所以只需要验证正方形和长方形就行了。
所以,我们只需要验证:
周长相等的三角形里等边三角形的面积最大。
周长相等的四边形里正方形的面积最大。
周长相等的圆和半圆、扇形等比较,圆的面积最大。
为了使验证的数据,更有说服力,再增加正五边形和正六边形的验证。
让五个小组分别选择任务,并问学生们,要想完成你们组的任务需要那些材料?
教师出示准备的各种材料:长62.8厘米的铁丝若干,钳子、卷尺、计算器各若干个。
让各小组组长上台选材,完成任务单并讨论方案。
三.制定方案、合作实施
2.分工合作、完成任务
学生开展小组活动,教师巡回并在必要的时候提供指导性帮助,并关注合理分工。
预估方案:
(1)验证:周长相等的三角形里等边三角形的面积最大。
(2)验证:周长相等的四边形里正方形的面积最大。
(3)验证周长相等的圆和半圆、扇形等比较,圆的面积最大。
(4)验证:周长相等的五边形里正五边形的面积最大。
(5)验证:周长相等的六边形里正六边形的面积最大。
四.小组汇报、得出结论
1.各小组上台展示、汇报交流并互相评价,最终得出结论。
通过汇报比较,得出结论。
(1)周长相等的三角形里等边三角形的面积最大。
(2)周长相等的四边形里正方形的面积最大。
(3)周长相等的圆和半圆、扇形等比较,圆的面积最大。
(4)周长相等的五边形里正五边形的面积最大。
(5)周长相等的六边形里正六边形的面积最大。
即:周长一定, 1.在边数相等的情况下正多边形的面积最大。
2.正多边形的面积随着边数的增加而增加,当边数趋近于正无穷时面积最大值,即为圆。
五.知识应用
根据得出的规律,引导学生解释生活中的问题或者一些自然规律。例如,蒙古包的底部为什么是圆形的?为什么绝大数根和茎的横截面是圆形的?
六.课堂小结
教师小结。启发学生运用所学知识解决生活中的更多的问题,让数学知识应用于生活。
学习目标
引导学生基于真实的情境任务——猪圈围成什么形状既能节省成本,又能围的面积最大呢?针对这一驱动性问题,展开讨论探究。使学生发现解决这一驱动性问题也就是解决“周长相等的平面图形,谁的面积最大?”这一问题。接下来,引导学生们借助已有的知识经验、生活经验经历从发现问题、分析问题、合作探究、解决问题的过程。在这一过程中融合各学科的知识,充分发挥小组合作的能力、动手操作能力,培养了学生们综合运用各学科知识与方法解决实际问题的能力。与此同时,培养了学生们的问题意识、应用意识和创新意识,为今后的学习积累活动经验,不断提高解决现实问题的能力。
驱动性问题
猪圈围成什么形状既能节省成本,又能围的面积最大呢?
学习任务设计与实施
学习任务设计:
这节课首先结合“由于当前猪肉等农产品大幅上涨,农场主想扩大自己的养殖规模。”这一真实情景,提出驱动性问题“猪圈围成什么形状既能节省成本,又能围的面积最大呢?”首先引导学生将驱动性问题转化成数学问题“周长相等的平面图形,谁的面积最大?”然后,引导学生们结合自己的各学科知识经验展开思考、讨论,并且小组合作选取材料、工具进行探究、操作,然后得出结论、汇报,最后进行评价。在整个的过程中,培养了学生们的问题意识、应用意识和创新意识,为今后的学习积累活动经验,不断提高解决现实问题的能力。
项目实施:
一. 情境导入,引出驱动性问题
首先,出示某种商品2019年价格走势图,让学生猜测这是哪种商品。
引出答案,这是2019年猪肉价格的年走势图。
师:看到这个走势图,你有什么想法?学生各抒己见。
师:由于当前猪肉等农产品大幅上涨,农场主想扩大自己的养殖规模。所以就需要盖猪圈,猪圈围成什么形状既能节省成本,又能围的面积最大呢?
教师引导学生将这一问题转化成数学问题“周长相等的平面图形,谁的面积最大?”
二. 头脑风暴
在没有任何约束条件限制的情况下学生头脑风暴,提出了各种多样化的方法并及时探讨方法的可行性。有的同学会想到猪圈的材料选择、高度、围成的形状等问题。为了缩短项目的时间,教师加上条件限制,如果猪圈的高度和材料一定的情况下,我们怎么样满足农场主的要求。从而引导学生将农场主的问题转化成数学问题“周长相等的平面图形,谁的面积最大?”针对这样一个问题,有的同学认为,把图形的周长假设成一个固定的值,求出面积就可以,但是发现假设数据只能求出圆和正方形的面积。所以,最后统一思路,要想解决这个问题,必须通过在操作中实际测量数据求面积,也就是利用一根固定长度的铁丝,围成平面图形,然后计算平面图形面积,并对比各种图形面积的大小。
各小组继续讨论交流,并猜测围成哪一种平面图形面积最大。
教师课件学过求面积的图形。
(三角形、正方形、长方形、平行四边形、梯形、圆形。)
当猜测到圆的面积时,教师可以结合翻转课堂的小视频给学生们进行学习。
接下来各小组选择自己小组要验证的图形,进行操作。
师:如果要围成三角形,你认为围成什么三角形更有优势?
生:等边三角形!师:那就需要我们操作验证了。
师:那么,对于四边形我们是不是都要验证?
通过平行四边形扣条学具和课件演示,引导学生发现平行四边形和梯形都没有长方形有优势,所以只需要验证正方形和长方形就行了。
所以,我们只需要验证:
周长相等的三角形里等边三角形的面积最大。
周长相等的四边形里正方形的面积最大。
周长相等的圆和半圆、扇形等比较,圆的面积最大。
为了使验证的数据,更有说服力,再增加正五边形和正六边形的验证。
让五个小组分别选择任务,并问学生们,要想完成你们组的任务需要那些材料?
教师出示准备的各种材料:长62.8厘米的铁丝若干,钳子、卷尺、计算器各若干个。
让各小组组长上台选材,完成任务单并讨论方案。
三.制定方案、合作实施
2.分工合作、完成任务
学生开展小组活动,教师巡回并在必要的时候提供指导性帮助,并关注合理分工。
预估方案:
(1)验证:周长相等的三角形里等边三角形的面积最大。
(2)验证:周长相等的四边形里正方形的面积最大。
(3)验证周长相等的圆和半圆、扇形等比较,圆的面积最大。
(4)验证:周长相等的五边形里正五边形的面积最大。
(5)验证:周长相等的六边形里正六边形的面积最大。
四.小组汇报、得出结论
1.各小组上台展示、汇报交流并互相评价,最终得出结论。
通过汇报比较,得出结论。
(1)周长相等的三角形里等边三角形的面积最大。
(2)周长相等的四边形里正方形的面积最大。
(3)周长相等的圆和半圆、扇形等比较,圆的面积最大。
(4)周长相等的五边形里正五边形的面积最大。
(5)周长相等的六边形里正六边形的面积最大。
即:周长一定, 1.在边数相等的情况下正多边形的面积最大。
2.正多边形的面积随着边数的增加而增加,当边数趋近于正无穷时面积最大值,即为圆。
五.知识应用
根据得出的规律,引导学生解释生活中的问题或者一些自然规律。例如,蒙古包的底部为什么是圆形的?为什么绝大数根和茎的横截面是圆形的?
六.课堂小结
教师小结。启发学生运用所学知识解决生活中的更多的问题,让数学知识应用于生活。
