北师大版高中数学必修三 3.3模拟方法――概率的应用 第二课时教案
文档属性
| 名称 | 北师大版高中数学必修三 3.3模拟方法――概率的应用 第二课时教案 | 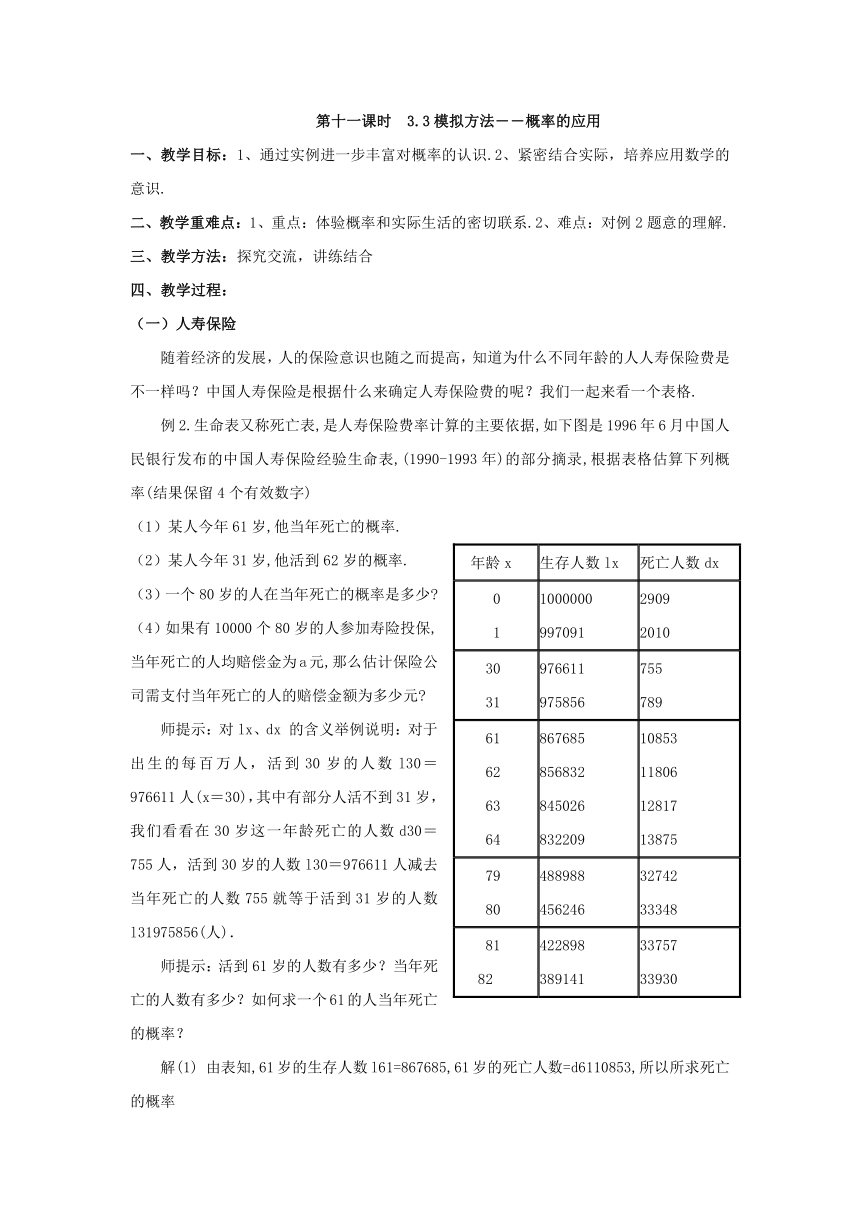 | |
| 格式 | zip | ||
| 文件大小 | 25.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 17:04:34 | ||
图片预览

文档简介
第十一课时
3.3模拟方法――概率的应用
一、教学目标:1、通过实例进一步丰富对概率的认识.2、紧密结合实际,培养应用数学的意识.
二、教学重难点:1、重点:体验概率和实际生活的密切联系.2、难点:对例2题意的理解.
三、教学方法:探究交流,讲练结合
四、教学过程:
(一)人寿保险
随着经济的发展,人的保险意识也随之而提高,知道为什么不同年龄的人人寿保险费是不一样吗?中国人寿保险是根据什么来确定人寿保险费的呢?我们一起来看一个表格.
例2.生命表又称死亡表,是人寿保险费率计算的主要依据,如下图是1996年6月中国人民银行发布的中国人寿保险经验生命表,(1990-1993年)的部分摘录,根据表格估算下列概率(结果保留4个有效数字)
年龄x
生存人数lx
死亡人数dx
0
1
1000000
997091
2909
2010
30
31
976611
975856
755
789
61
62
63
64
867685
856832
845026
832209
10853
11806
12817
13875
79
80
488988
456246
32742
33348
81
82
422898
389141
33757
33930
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
(3)一个80岁的人在当年死亡的概率是多少?
(4)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?
师提示:对lx、dx
的含义举例说明:对于出生的每百万人,活到30岁的人数l30=976611人(x=30),其中有部分人活不到31岁,我们看看在30岁这一年龄死亡的人数d30=755人,活到30岁的人数l30=976611人减去当年死亡的人数755就等于活到31岁的人数l31975856(人).
师提示:活到61岁的人数有多少?当年死亡的人数有多少?如何求一个61的人当年死亡的概率?
解(1)
由表知,61岁的生存人数l61=867685,61岁的死亡人数=d6110853,所以所求死亡的概率
师提示:活到30岁的人数有多少?其中能活到62岁的人有多少?一个31岁的人能活到62岁的概率怎么求?
2)
由表知,l31=975856,
l62=856832,所以所求的概率:
(二)交通事故
寿命的增长、保险意识的提高侧面反映了社会经济的飞速发展;经济的发展,带动了道路建设,交通发展,从而安全隐患随之增长.请看:
据统计,2004年浙江省交通事故死亡人数为7549人,其中属于机动车驾驶人的交通违法行为原因造成死亡人数为6457.
看到这组数据,你有何感受?
多么可怕的一组数据,请同学们用所学知识根据这组数据来分析两个小问题:
(1)估计交通事故死亡1人,属于机动车驾驶人的交通违法行为原因的概率是多少(结果保留3个有效数字)?
(2)估计交通事故死亡2000人中,属于机动国驾驶人的交通违法行为原因的有多少人?
生练,指名板演.
你看到你分析所得的报告,你想说什么?
据统计,2006年我们温州,仅交通事故就死了762人,其中三分之一多发生在农村道路上.希望同学们在路上多多注意安全.做到“一慢、二看、三行”.
(三)私家车发展
交通工具的发展,莫过于私家车的发展,私家车快速走入千家万户,已成为汽车快速增长的主要推动力量.那么私家车的主人们是不是都有做到安全措施呢?
九年级三班同学作了关于私家车乘坐人数的统计,在100辆私家车中,统计结果如下表:
每辆私家车乘客数目
1
2
3
4
5
私家车数目
58
27
8
4
3
根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少?
(四)中场休息:欣赏三洋湿地风景
是哪儿?!经济的飞速发展势必会带动旅游业的成长,我们三洋这块温州的“绿肺”在若干年后势必会大放异彩.所以我们要共同来保护我们家乡的环境.
(五)垃圾分类
垃圾可以分为有机垃圾、无机垃圾与有害垃圾三类.为了有效地保护环境,居委会倡议居民将日常生活中产生的垃圾进行分类投放.一天,小林把垃圾分装在三个袋中,可他在投放时不小心把三个袋子都放错了位置.你能确定小林是怎样投放的吗?如果一个人任意投放,把三个袋子都放错位置的概率是多少?
(六)乘车问题
等若干年后,三洋湿地成了一道美丽的风景,来此观光游玩的人络绎不绝,假设以后每天某一时段开往三洋湿地有三辆专车(票价相同),有两人相约来我们三洋湿地游玩,但是他们不知道这些车的舒适程度,也不知道专车开过来的顺序,两人采用了不同的乘车方案:
甲:无论如何总是上开来的第一辆车,
乙:先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆车的舒适程度比第一辆好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.
如果把这三辆车的舒适程度分为上、中、下三等,请同学们尝试着解决下面的问题:
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙采用的方案,哪一种方案使自己乘上等车的可能性大?为什么?
(七)交流:本节课你有哪些收获?有何感想?
五、作业:课本:P155
B组2、3
六、教学反思:
3.3模拟方法――概率的应用
一、教学目标:1、通过实例进一步丰富对概率的认识.2、紧密结合实际,培养应用数学的意识.
二、教学重难点:1、重点:体验概率和实际生活的密切联系.2、难点:对例2题意的理解.
三、教学方法:探究交流,讲练结合
四、教学过程:
(一)人寿保险
随着经济的发展,人的保险意识也随之而提高,知道为什么不同年龄的人人寿保险费是不一样吗?中国人寿保险是根据什么来确定人寿保险费的呢?我们一起来看一个表格.
例2.生命表又称死亡表,是人寿保险费率计算的主要依据,如下图是1996年6月中国人民银行发布的中国人寿保险经验生命表,(1990-1993年)的部分摘录,根据表格估算下列概率(结果保留4个有效数字)
年龄x
生存人数lx
死亡人数dx
0
1
1000000
997091
2909
2010
30
31
976611
975856
755
789
61
62
63
64
867685
856832
845026
832209
10853
11806
12817
13875
79
80
488988
456246
32742
33348
81
82
422898
389141
33757
33930
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
(3)一个80岁的人在当年死亡的概率是多少?
(4)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?
师提示:对lx、dx
的含义举例说明:对于出生的每百万人,活到30岁的人数l30=976611人(x=30),其中有部分人活不到31岁,我们看看在30岁这一年龄死亡的人数d30=755人,活到30岁的人数l30=976611人减去当年死亡的人数755就等于活到31岁的人数l31975856(人).
师提示:活到61岁的人数有多少?当年死亡的人数有多少?如何求一个61的人当年死亡的概率?
解(1)
由表知,61岁的生存人数l61=867685,61岁的死亡人数=d6110853,所以所求死亡的概率
师提示:活到30岁的人数有多少?其中能活到62岁的人有多少?一个31岁的人能活到62岁的概率怎么求?
2)
由表知,l31=975856,
l62=856832,所以所求的概率:
(二)交通事故
寿命的增长、保险意识的提高侧面反映了社会经济的飞速发展;经济的发展,带动了道路建设,交通发展,从而安全隐患随之增长.请看:
据统计,2004年浙江省交通事故死亡人数为7549人,其中属于机动车驾驶人的交通违法行为原因造成死亡人数为6457.
看到这组数据,你有何感受?
多么可怕的一组数据,请同学们用所学知识根据这组数据来分析两个小问题:
(1)估计交通事故死亡1人,属于机动车驾驶人的交通违法行为原因的概率是多少(结果保留3个有效数字)?
(2)估计交通事故死亡2000人中,属于机动国驾驶人的交通违法行为原因的有多少人?
生练,指名板演.
你看到你分析所得的报告,你想说什么?
据统计,2006年我们温州,仅交通事故就死了762人,其中三分之一多发生在农村道路上.希望同学们在路上多多注意安全.做到“一慢、二看、三行”.
(三)私家车发展
交通工具的发展,莫过于私家车的发展,私家车快速走入千家万户,已成为汽车快速增长的主要推动力量.那么私家车的主人们是不是都有做到安全措施呢?
九年级三班同学作了关于私家车乘坐人数的统计,在100辆私家车中,统计结果如下表:
每辆私家车乘客数目
1
2
3
4
5
私家车数目
58
27
8
4
3
根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少?
(四)中场休息:欣赏三洋湿地风景
是哪儿?!经济的飞速发展势必会带动旅游业的成长,我们三洋这块温州的“绿肺”在若干年后势必会大放异彩.所以我们要共同来保护我们家乡的环境.
(五)垃圾分类
垃圾可以分为有机垃圾、无机垃圾与有害垃圾三类.为了有效地保护环境,居委会倡议居民将日常生活中产生的垃圾进行分类投放.一天,小林把垃圾分装在三个袋中,可他在投放时不小心把三个袋子都放错了位置.你能确定小林是怎样投放的吗?如果一个人任意投放,把三个袋子都放错位置的概率是多少?
(六)乘车问题
等若干年后,三洋湿地成了一道美丽的风景,来此观光游玩的人络绎不绝,假设以后每天某一时段开往三洋湿地有三辆专车(票价相同),有两人相约来我们三洋湿地游玩,但是他们不知道这些车的舒适程度,也不知道专车开过来的顺序,两人采用了不同的乘车方案:
甲:无论如何总是上开来的第一辆车,
乙:先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆车的舒适程度比第一辆好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车.
如果把这三辆车的舒适程度分为上、中、下三等,请同学们尝试着解决下面的问题:
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙采用的方案,哪一种方案使自己乘上等车的可能性大?为什么?
(七)交流:本节课你有哪些收获?有何感想?
五、作业:课本:P155
B组2、3
六、教学反思:
