北师大版六年级数学上期末复习第九讲数据处理(一)同步学案
文档属性
| 名称 | 北师大版六年级数学上期末复习第九讲数据处理(一)同步学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九讲
数据处理(一)
【考点解读1】三种简单统计图:扇形图、折线图、条形图
1.扇形图:用来表示整体与部分的关系。例如反映笑笑家食品支出占全部支出的多少,最好用扇形图表示。
2.折线图:表示数量的多少、增减变化。例如:画出1996年到2012年这期间举办的世界奥运会的中国所获得的金牌得数。
3.条形统计图:表示各个量的多少。例如反应某校六年级各班的人数,用条形统计图。
【典例解析1】
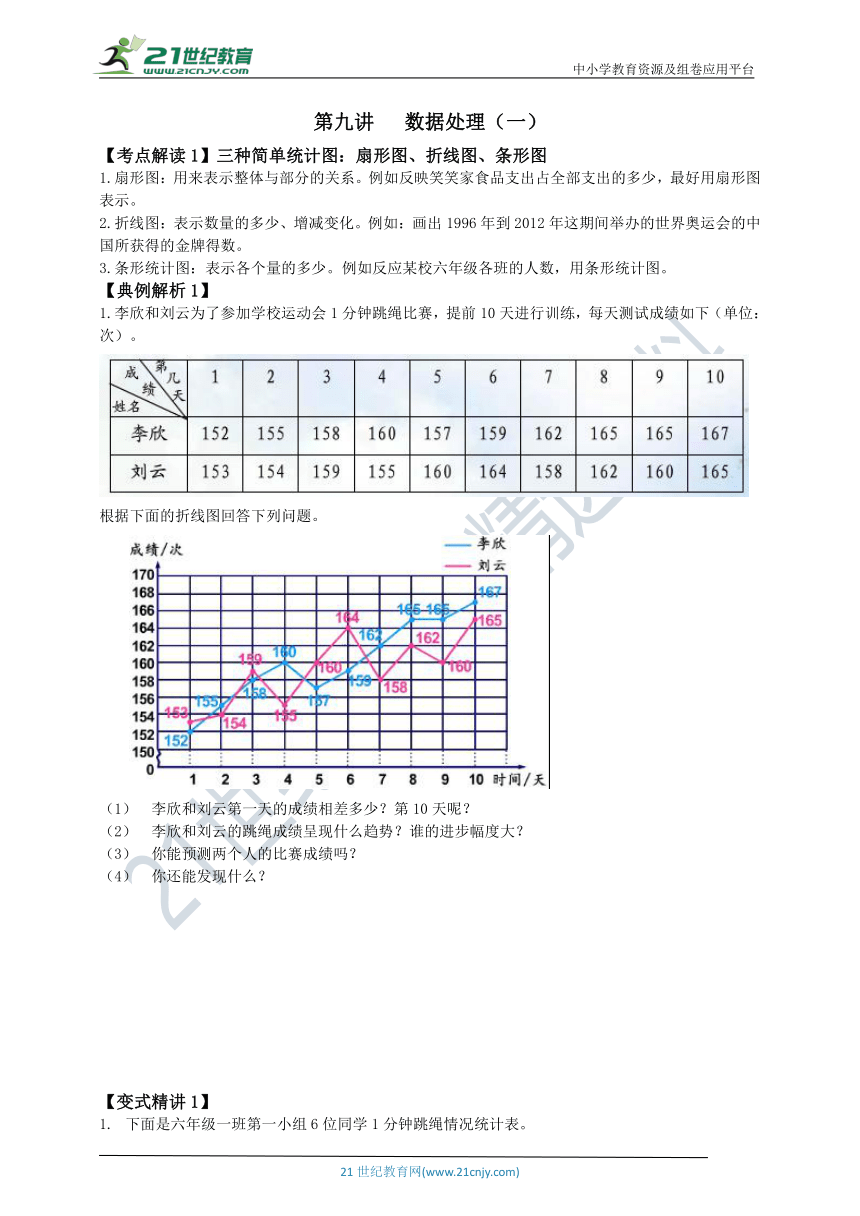
1.李欣和刘云为了参加学校运动会1分钟跳绳比赛,提前10天进行训练,每天测试成绩如下(单位:次)。
根据下面的折线图回答下列问题。
李欣和刘云第一天的成绩相差多少?第10天呢?
李欣和刘云的跳绳成绩呈现什么趋势?谁的进步幅度大?
你能预测两个人的比赛成绩吗?
你还能发现什么?
【变式精讲1】
下面是六年级一班第一小组6位同学1分钟跳绳情况统计表。
这组数据的中位数是多少?众数是多少?
平均每分钟跳绳多少下?
你认为平均数和中位数中,哪个更能反映出这组同学跳绳的整体水平?
根据统计表画成条形统计图。
【考题演练1】
一、选择题。
1.要统计一个病人一天内的体温变化情况,应该选用(
)。
A.条形统计图
B.折线统计图
C.扇形统计图
2.为了反映数量增减变化情况,应该选用(
)统计图。
A.条形
B.折线
C.扇形
3.根据下面的统计图与统计表回答问题。
各类员工工资这组数据的平均数、中位数和众数各是多少?
你认为哪个数据能代表这个公司人员工资的一般水平比较合适?
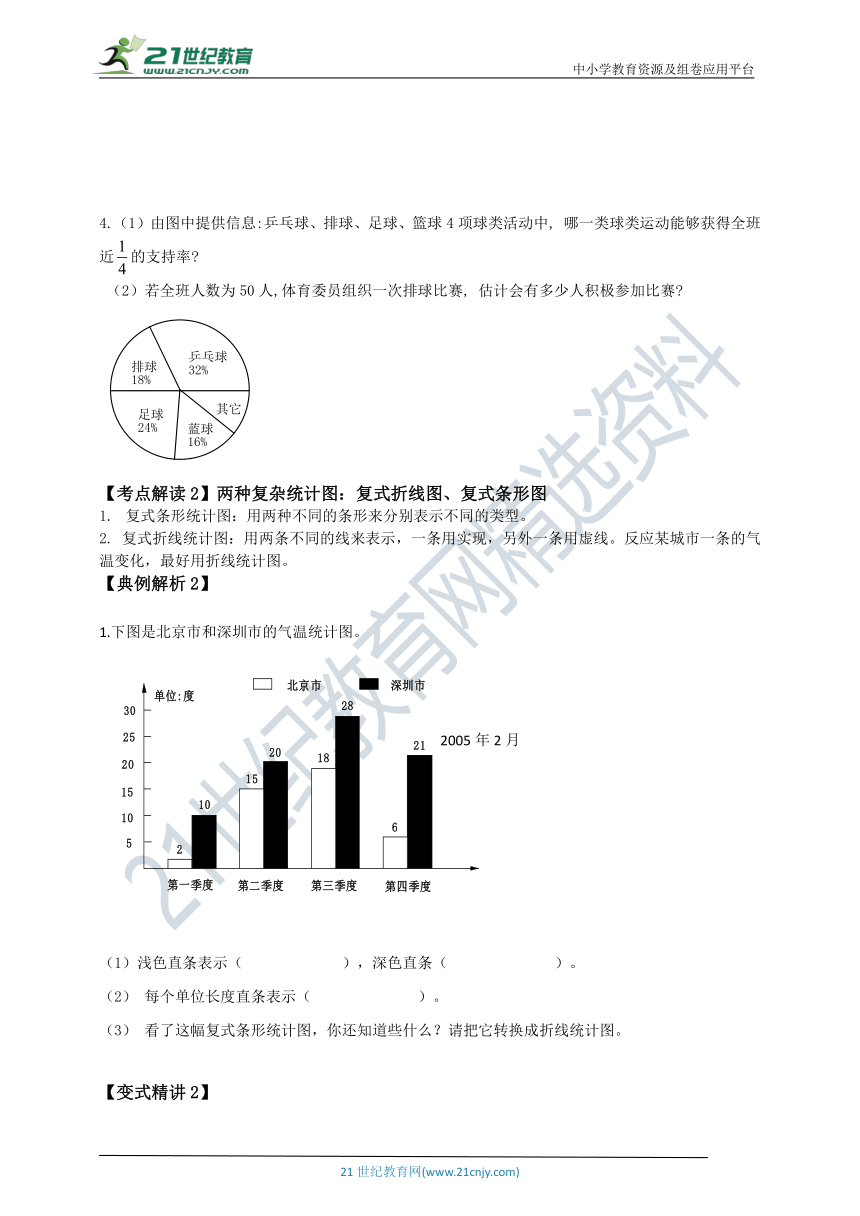
4.(1)由图中提供信息:乒乓球、排球、足球、篮球4项球类活动中,
哪一类球类运动能够获得全班近的支持率?
(2)若全班人数为50人,体育委员组织一次排球比赛,
估计会有多少人积极参加比赛?
【考点解读2】两种复杂统计图:复式折线图、复式条形图
复式条形统计图:用两种不同的条形来分别表示不同的类型。
2.
复式折线统计图:用两条不同的线来表示,一条用实现,另外一条用虚线。反应某城市一条的气温变化,最好用折线统计图。
【典例解析2】
1.下图是北京市和深圳市的气温统计图。
2005年2月
(1)浅色直条表示(
),深色直条(
)。
(2)
每个单位长度直条表示(
)。
(3)
看了这幅复式条形统计图,你还知道些什么?请把它转换成折线统计图。
【变式精讲2】
1.
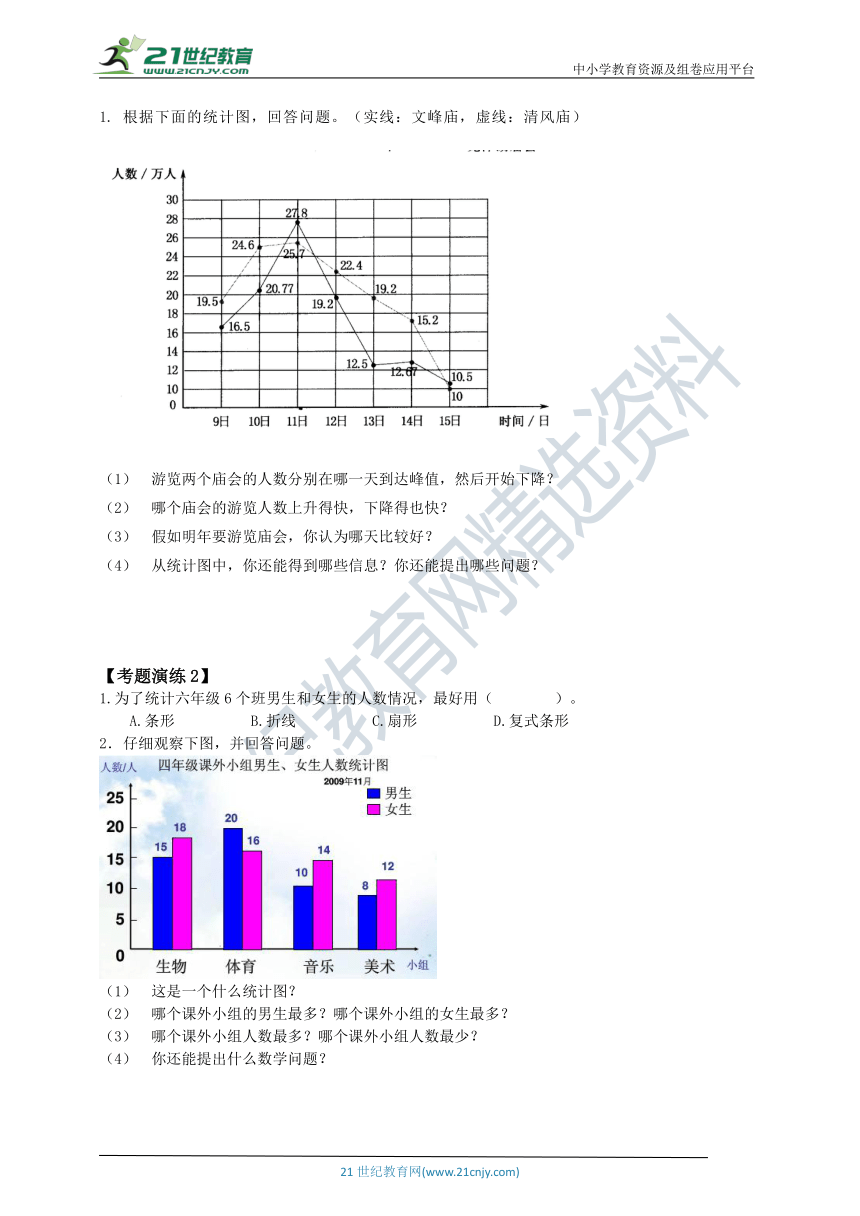
根据下面的统计图,回答问题。(实线:文峰庙,虚线:清风庙)
游览两个庙会的人数分别在哪一天到达峰值,然后开始下降?
哪个庙会的游览人数上升得快,下降得也快?
假如明年要游览庙会,你认为哪天比较好?
从统计图中,你还能得到哪些信息?你还能提出哪些问题?
【考题演练2】
1.为了统计六年级6个班男生和女生的人数情况,最好用(
)。
A.条形
B.折线
C.扇形
D.复式条形
2.仔细观察下图,并回答问题。
这是一个什么统计图?
哪个课外小组的男生最多?哪个课外小组的女生最多?
哪个课外小组人数最多?哪个课外小组人数最少?
你还能提出什么数学问题?
3.
下图是深圳某公司一车间中三个小组男、女工人数统计图
(1)男工人数最多的是(
)小组,最少的是(
)小组;
女工人数最多的是(
)小组,最少的是(
)小组;
从图上可以看出(
)小组的人数最多,(
)小组的人数最少.
(2)通过计算,能知道第一小组是(
)人,人数最少;第二小组是(
)人,人数最多;第三小组是(
)人.
(3)第一小组男工人数是女工人数的(
)倍。
(4)第二小组男工人数占第二小组人数的(
)。
(5)全车间有工人(
)人,其中女工(
)人,占(
)。
(6)第一小组女工人数比男工人数少(
)%
。
(7)
全车间男工人数比女工人数多(
)%。
【考点解读3】中位数、众数、平均数
平均数:几个数量的和除以数量的个数;
中位数:数据从大到小或从小到大排列,最中间的一个或最中间的两个的平均数。
众数:在一组数据中出现次数最多的数。
【典例解析3】
1.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下:9.8,9.7,9.7,9.6,9.6,9.6,9.6,9.5,9.4,9.4,9.1
(1)这组数据的平均数、中位数和众数各是多少?
(2)如果按照“去掉一个最高分,去掉一个最低分”的评分的方法来计算,平均分是多少?你认为是否有道理?为什么?
【变式精讲3】
1.某家电器商场,3月份销售电器如下:
这个商场销售的家电的单价的中位数和众数分别是多少?
中央为了关心“三农”,购买一台彩电补贴10%,一台冰箱补贴15%,一台空调补贴18%,小明家购买了一台彩电一台冰箱,实际付了多少元?
【考题演练3】
一、选择题。
1.妈妈经销儿童鞋,小华帮妈妈随机调查了全班9名女生的的鞋子尺码:23、20、22、21、22、22、22、34、22,妈妈最感兴趣的是这组数据的(
)。
A.平均数
B.中位数
C.众数
2.小雅五次数学成绩分别是89分,96分,89分,85分,陈老师想了解小雅的数学成绩变化情况,他最关心的应是(
)。
A.平均数
B.中位数
C.众数
3.已知一组数据为0、1、4、a、6、13,这组数据的中位数是5,那么这组数据的平均数是(
)。
A.4
B.5
C.5.8
D.6
4.一组数据:10,15,18,25,32,34,48,50,中位数是(
)。
A.25
B.28.5
C.32
二、计算。
1.学校艺术节,美术组的同学在某画展中心进行了为期一周的作品展览,社会反响很大,同学们对每天参加的人数进行了统计,数据如下:
这组数据的众数和中位数是(
)。
A.1.2,1.8
B.1.8,1.8
C.1.8,1.2
D.1.2,1.2
2.小明家去年上半年每月用电情况如下表(用电量单位:千瓦时)
求出上半年每月平均用电量是多少千瓦时?
这些数据的中位数是多少?为什么中位数比平均数小?
六年级普数(上)
第九讲(参考答案)
【典例解析1】
1.(1)1,2
(2)李欣呈稳定上升趋势,刘云呈振荡上升;李欣进步大
(3)李欣的成绩高于刘云
(4)从第7天开始,李欣的成绩都比刘云的成绩好
【变式精讲1】
(1)180、180
(2)165
(3)中位数
(4)略
【考题演练1】
1.B
2.B
3.(1)平均数:1112.5,中位数:600,众数:600
(2)众数
4.(1)足球
(2)50×18%=9(人)
【典例解析2】
1.(1)北京市的气温、深圳市的气温
(2)5度
(3)北京市的温度比深圳市的温度低,而且北京的气温变化差距小于深圳市的气温变化。折线图略
【变式精讲2】
(1)游览文峰庙和清风庙的人数都在11日达到峰值,然后开始下降
(2)文峰庙的人数上升得快,下降得也快
(3)15日最好,因为这天人数最少
(4)清风庙游览人数相对于文峰庙人数较多。
【考题演练2】
1.D
2.(1)复式条形统计图
(2)体育课外小组的男生最多,生物课外小组的女生人数最多
(3)体育课外小组人数最多,美术课外小组人数最少
(4)其中男生有53人,女生有60人
3.
(1)第三、第一、第二、第一、第二、第一
(2)110、250、320
(3)8/3
(4)11/25
(5)580、250、25/58
(6)62.5%
(7)32%
【典例解析3】
1.(1)平均数:9.55
中位数:9.6
众数:9.6
(2)平均分:9.57,有道理
【变式精讲3】
1.(1)中位数:2000
众数:2400
(2)3880元
【考题演练3】
一、选择题。
1.C
2.A
3.B
4.B
二、计算。
1.D
2.(1)66
(2)64、因为所有用电量低于平均数占多数
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第九讲
数据处理(一)
【考点解读1】三种简单统计图:扇形图、折线图、条形图
1.扇形图:用来表示整体与部分的关系。例如反映笑笑家食品支出占全部支出的多少,最好用扇形图表示。
2.折线图:表示数量的多少、增减变化。例如:画出1996年到2012年这期间举办的世界奥运会的中国所获得的金牌得数。
3.条形统计图:表示各个量的多少。例如反应某校六年级各班的人数,用条形统计图。
【典例解析1】
1.李欣和刘云为了参加学校运动会1分钟跳绳比赛,提前10天进行训练,每天测试成绩如下(单位:次)。
根据下面的折线图回答下列问题。
李欣和刘云第一天的成绩相差多少?第10天呢?
李欣和刘云的跳绳成绩呈现什么趋势?谁的进步幅度大?
你能预测两个人的比赛成绩吗?
你还能发现什么?
【变式精讲1】
下面是六年级一班第一小组6位同学1分钟跳绳情况统计表。
这组数据的中位数是多少?众数是多少?
平均每分钟跳绳多少下?
你认为平均数和中位数中,哪个更能反映出这组同学跳绳的整体水平?
根据统计表画成条形统计图。
【考题演练1】
一、选择题。
1.要统计一个病人一天内的体温变化情况,应该选用(
)。
A.条形统计图
B.折线统计图
C.扇形统计图
2.为了反映数量增减变化情况,应该选用(
)统计图。
A.条形
B.折线
C.扇形
3.根据下面的统计图与统计表回答问题。
各类员工工资这组数据的平均数、中位数和众数各是多少?
你认为哪个数据能代表这个公司人员工资的一般水平比较合适?
4.(1)由图中提供信息:乒乓球、排球、足球、篮球4项球类活动中,
哪一类球类运动能够获得全班近的支持率?
(2)若全班人数为50人,体育委员组织一次排球比赛,
估计会有多少人积极参加比赛?
【考点解读2】两种复杂统计图:复式折线图、复式条形图
复式条形统计图:用两种不同的条形来分别表示不同的类型。
2.
复式折线统计图:用两条不同的线来表示,一条用实现,另外一条用虚线。反应某城市一条的气温变化,最好用折线统计图。
【典例解析2】
1.下图是北京市和深圳市的气温统计图。
2005年2月
(1)浅色直条表示(
),深色直条(
)。
(2)
每个单位长度直条表示(
)。
(3)
看了这幅复式条形统计图,你还知道些什么?请把它转换成折线统计图。
【变式精讲2】
1.
根据下面的统计图,回答问题。(实线:文峰庙,虚线:清风庙)
游览两个庙会的人数分别在哪一天到达峰值,然后开始下降?
哪个庙会的游览人数上升得快,下降得也快?
假如明年要游览庙会,你认为哪天比较好?
从统计图中,你还能得到哪些信息?你还能提出哪些问题?
【考题演练2】
1.为了统计六年级6个班男生和女生的人数情况,最好用(
)。
A.条形
B.折线
C.扇形
D.复式条形
2.仔细观察下图,并回答问题。
这是一个什么统计图?
哪个课外小组的男生最多?哪个课外小组的女生最多?
哪个课外小组人数最多?哪个课外小组人数最少?
你还能提出什么数学问题?
3.
下图是深圳某公司一车间中三个小组男、女工人数统计图
(1)男工人数最多的是(
)小组,最少的是(
)小组;
女工人数最多的是(
)小组,最少的是(
)小组;
从图上可以看出(
)小组的人数最多,(
)小组的人数最少.
(2)通过计算,能知道第一小组是(
)人,人数最少;第二小组是(
)人,人数最多;第三小组是(
)人.
(3)第一小组男工人数是女工人数的(
)倍。
(4)第二小组男工人数占第二小组人数的(
)。
(5)全车间有工人(
)人,其中女工(
)人,占(
)。
(6)第一小组女工人数比男工人数少(
)%
。
(7)
全车间男工人数比女工人数多(
)%。
【考点解读3】中位数、众数、平均数
平均数:几个数量的和除以数量的个数;
中位数:数据从大到小或从小到大排列,最中间的一个或最中间的两个的平均数。
众数:在一组数据中出现次数最多的数。
【典例解析3】
1.在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下:9.8,9.7,9.7,9.6,9.6,9.6,9.6,9.5,9.4,9.4,9.1
(1)这组数据的平均数、中位数和众数各是多少?
(2)如果按照“去掉一个最高分,去掉一个最低分”的评分的方法来计算,平均分是多少?你认为是否有道理?为什么?
【变式精讲3】
1.某家电器商场,3月份销售电器如下:
这个商场销售的家电的单价的中位数和众数分别是多少?
中央为了关心“三农”,购买一台彩电补贴10%,一台冰箱补贴15%,一台空调补贴18%,小明家购买了一台彩电一台冰箱,实际付了多少元?
【考题演练3】
一、选择题。
1.妈妈经销儿童鞋,小华帮妈妈随机调查了全班9名女生的的鞋子尺码:23、20、22、21、22、22、22、34、22,妈妈最感兴趣的是这组数据的(
)。
A.平均数
B.中位数
C.众数
2.小雅五次数学成绩分别是89分,96分,89分,85分,陈老师想了解小雅的数学成绩变化情况,他最关心的应是(
)。
A.平均数
B.中位数
C.众数
3.已知一组数据为0、1、4、a、6、13,这组数据的中位数是5,那么这组数据的平均数是(
)。
A.4
B.5
C.5.8
D.6
4.一组数据:10,15,18,25,32,34,48,50,中位数是(
)。
A.25
B.28.5
C.32
二、计算。
1.学校艺术节,美术组的同学在某画展中心进行了为期一周的作品展览,社会反响很大,同学们对每天参加的人数进行了统计,数据如下:
这组数据的众数和中位数是(
)。
A.1.2,1.8
B.1.8,1.8
C.1.8,1.2
D.1.2,1.2
2.小明家去年上半年每月用电情况如下表(用电量单位:千瓦时)
求出上半年每月平均用电量是多少千瓦时?
这些数据的中位数是多少?为什么中位数比平均数小?
六年级普数(上)
第九讲(参考答案)
【典例解析1】
1.(1)1,2
(2)李欣呈稳定上升趋势,刘云呈振荡上升;李欣进步大
(3)李欣的成绩高于刘云
(4)从第7天开始,李欣的成绩都比刘云的成绩好
【变式精讲1】
(1)180、180
(2)165
(3)中位数
(4)略
【考题演练1】
1.B
2.B
3.(1)平均数:1112.5,中位数:600,众数:600
(2)众数
4.(1)足球
(2)50×18%=9(人)
【典例解析2】
1.(1)北京市的气温、深圳市的气温
(2)5度
(3)北京市的温度比深圳市的温度低,而且北京的气温变化差距小于深圳市的气温变化。折线图略
【变式精讲2】
(1)游览文峰庙和清风庙的人数都在11日达到峰值,然后开始下降
(2)文峰庙的人数上升得快,下降得也快
(3)15日最好,因为这天人数最少
(4)清风庙游览人数相对于文峰庙人数较多。
【考题演练2】
1.D
2.(1)复式条形统计图
(2)体育课外小组的男生最多,生物课外小组的女生人数最多
(3)体育课外小组人数最多,美术课外小组人数最少
(4)其中男生有53人,女生有60人
3.
(1)第三、第一、第二、第一、第二、第一
(2)110、250、320
(3)8/3
(4)11/25
(5)580、250、25/58
(6)62.5%
(7)32%
【典例解析3】
1.(1)平均数:9.55
中位数:9.6
众数:9.6
(2)平均分:9.57,有道理
【变式精讲3】
1.(1)中位数:2000
众数:2400
(2)3880元
【考题演练3】
一、选择题。
1.C
2.A
3.B
4.B
二、计算。
1.D
2.(1)66
(2)64、因为所有用电量低于平均数占多数
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
