3.7切线长定理 同步练习(含详解)
文档属性
| 名称 | 3.7切线长定理 同步练习(含详解) |  | |
| 格式 | rar | ||
| 文件大小 | 418.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:52:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
*3.7切线长定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连结AC,则∠A的度数是( )
A.15° B.30° C.35° D.45°
2.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )
A.130° B.120° C.110° D.100°
3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
4.给出下列说法:
①任意一个三角形一定有一个外接圆,并且只有一个外接圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个内切圆,并且只有一个内切圆;
④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图 ,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠P=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.6 D.10
6.如图,已知⊙O分别与△ABC的BC边、AB的延长线、AC的延长线相切,则∠BOC等于( )
A.∠A B.90°+∠A C.90°-∠A D.180°-∠A
7.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
8.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
A.100° B.110° C.115° D.120°
二、填空题
9.如图,△ABC的边与⊙O分别相切于点D,E,F,且BD=3 cm,DC= 5 cm,△ABC的周长为22 cm,那么AB的长为______cm.
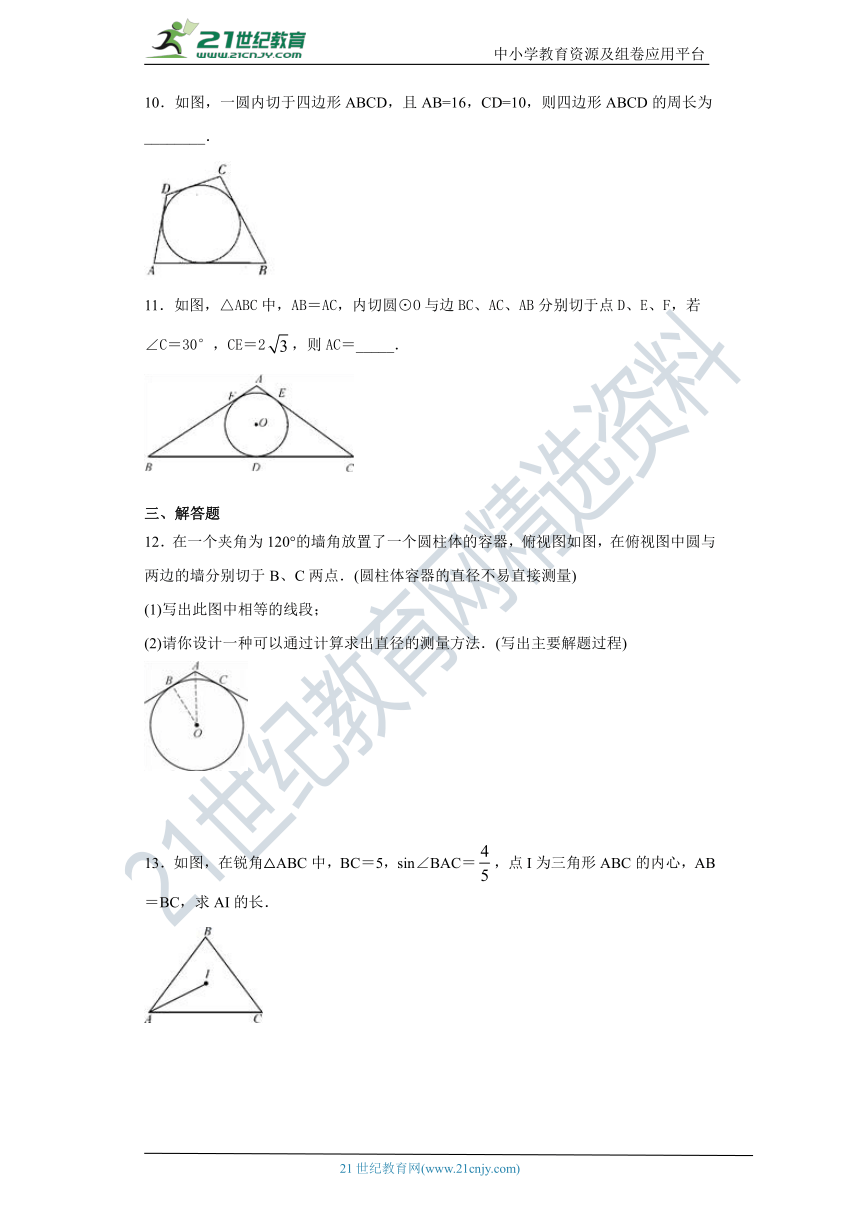
10.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
11.如图,△ABC中,AB=AC,内切圆⊙O与边BC、AC、AB分别切于点D、E、F,若∠C=30°,CE=2,则AC=_____.
三、解答题
12.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B、C两点.(圆柱体容器的直径不易直接测量)
(1)写出此图中相等的线段;
(2)请你设计一种可以通过计算求出直径的测量方法.(写出主要解题过程)
13.如图,在锐角△ABC中,BC=5,sin∠BAC=,点I为三角形ABC的内心,AB=BC,求AI的长.
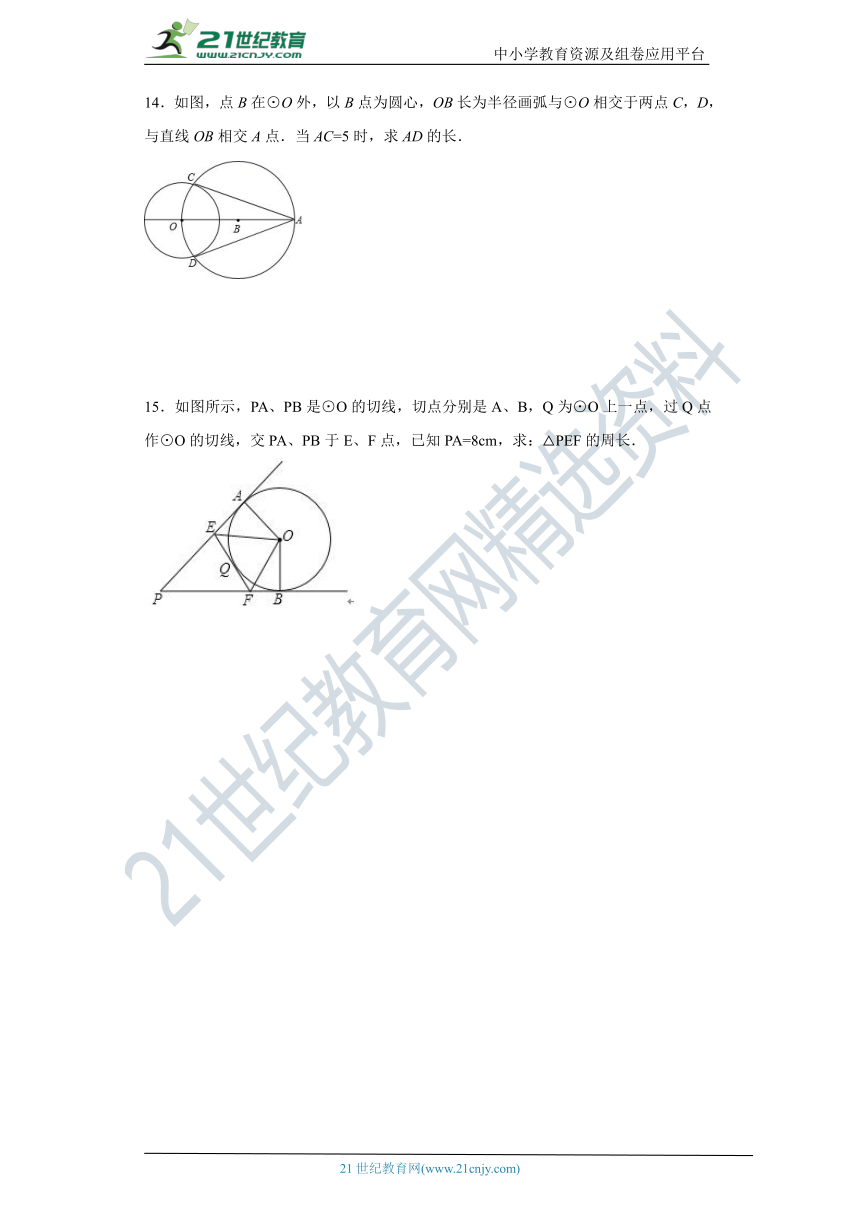
14.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.
15.如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.
?
参考答案
1.C
解析:
连接OC,
∵BD、CD分别是过⊙O上点B,C的切线,
∴OC⊥CD,OB⊥BD,
∴∠OCD=∠OBD=90,
∵∠BDC=110,
∴∠BOC=360?∠OCD?∠BDC?∠OBD=70,
∴∠A=∠BOC=35.
故选C.
2.C
解析:
∵AB、AC是⊙O的两条切线,B、C是切点,
∴∠B=∠C=90°,∠BOC=180°-∠A=110°.
故选C.
3.D
解析:
解:从圆心引3边垂线后,2直角边都被分为2截,直角处和2条从圆心引得半径形成正方形,2直角边剩余线段的和刚好为斜边长度
所以周长=1+1+8+8=18
4.B
解析:
三角形的外接圆是三条垂直平分线的交点,有且只有一个交点,所以任意三角形一定有一个外接圆,并且只有一个外接圆,①是对的;
圆的内接三角形可以无数多个,所以②是错的;
三角形的内切圆的圆心是三个内角平分线的交点,有且只有一个交点,所以任意一个三角形一定有一个内切圆,并且只有一个内切圆,③是对的;
圆的外切三角形可以有无数多个,④是错误的.
所以①③正确,正确的有2个.
故选B.
5.B
解析:
分析:根据切线的性质和∠P的度数得出△PAB为等边三角形,从而得出答案.
详解:∵PA和PB为切线, ∴PA=PB, ∵∠P=60°, ∴△PAB为等边三角形,
6.C
解析:设O分别与△ABC的BC边,AB的延长线,AC的延长线相切,切点分别为D,E,F,
∴OE⊥AB,OF⊥AC,
故选C.
7.B
解析:设分别是的切点,
是一张三角形的纸片, 是它的内切圆,点是其中的一个切点,
则
故
故选B.
8.B
解析:
如下图,连接AD,BD,
∵同弧所对的圆周角相等,∴∠ABD=∠AED=20°,
∵AB为直径,∴∠ADB=90°,
∴∠BAD=90°-20°=70°,
∴∠BCD=180°-70°=110°.
故选B
9.6
解析:
∵ △ABC的边与⊙O分别相切于点D,E,F,
∴BD=BE,CD=CF,AE=AF,
∴AB+AC+BC=AE+EB+BD+DC+CF+FA
=2AE+2DC+2BD
=2AE+10+6
=2AE+16
=22cm,
则AE=3cm,
∴AB=AE+BE=AE+BD=3+3=6cm.
故答案为:6.
10.52
解析:
根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=52
故填:52
11.4
解析:连接AO、OD;
∵O是△ABC的内心,
∴OA平分∠BAC,
∵⊙O是△ABC的内切圆,D是切点,
∴OD⊥BC;
又∵AC=AB,
∴A、O、D三点共线,即AD⊥BC,
∵CD、CE是⊙O的切线,
∴CD=CE=2,
在Rt△ACD中,由∠C=30°,CD=2,得
AC==4.
12.解析:(1)根据切线长定理,
知
(2)连接
在中,
∴圆的直径为
即只需测得的长,就可求得圆的直径.
点睛:切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
13.AI=.
解析:
连结CI,BI,且延长BI交AC于点F,过点I作IG⊥BC于点G,IE⊥AB于点E.∵AB=BC=5,点I为△ABC的内心,∴BF⊥AC,AF=CF.在Rt△ABF中,
∵sin∠BAC=,∴BF=4.∴AF==3,∴AC=6.∵点I是△ABC的内心,IE⊥AB,IF⊥AC,IG⊥BC,∴IE=IF=IG.∴S△ABC=AB+AC+BC)·IF=AC·BF,∴IF=,∴AI==.
14.5
解析:
解:连接OC、OD.
∵OA是⊙B的直径,
∴∠OCA=∠ODA=90°,
∴AC、AD都是⊙O的切线.
∴AD=AC=5.
15.16cm.
解析:
解:∵PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
∴PA=PB,EA=EQ,FB=FQ,
∵PA=8cm,
∴△PEF的周长为:PE+EF+PF=PA+PB=8+8=16(cm)
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
*3.7切线长定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连结AC,则∠A的度数是( )
A.15° B.30° C.35° D.45°
2.如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为( )
A.130° B.120° C.110° D.100°
3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
4.给出下列说法:
①任意一个三角形一定有一个外接圆,并且只有一个外接圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个内切圆,并且只有一个内切圆;
④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图 ,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠P=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.6 D.10
6.如图,已知⊙O分别与△ABC的BC边、AB的延长线、AC的延长线相切,则∠BOC等于( )
A.∠A B.90°+∠A C.90°-∠A D.180°-∠A
7.如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
8.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
A.100° B.110° C.115° D.120°
二、填空题
9.如图,△ABC的边与⊙O分别相切于点D,E,F,且BD=3 cm,DC= 5 cm,△ABC的周长为22 cm,那么AB的长为______cm.
10.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
11.如图,△ABC中,AB=AC,内切圆⊙O与边BC、AC、AB分别切于点D、E、F,若∠C=30°,CE=2,则AC=_____.
三、解答题
12.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B、C两点.(圆柱体容器的直径不易直接测量)
(1)写出此图中相等的线段;
(2)请你设计一种可以通过计算求出直径的测量方法.(写出主要解题过程)
13.如图,在锐角△ABC中,BC=5,sin∠BAC=,点I为三角形ABC的内心,AB=BC,求AI的长.
14.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.
15.如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.
?
参考答案
1.C
解析:
连接OC,
∵BD、CD分别是过⊙O上点B,C的切线,
∴OC⊥CD,OB⊥BD,
∴∠OCD=∠OBD=90,
∵∠BDC=110,
∴∠BOC=360?∠OCD?∠BDC?∠OBD=70,
∴∠A=∠BOC=35.
故选C.
2.C
解析:
∵AB、AC是⊙O的两条切线,B、C是切点,
∴∠B=∠C=90°,∠BOC=180°-∠A=110°.
故选C.
3.D
解析:
解:从圆心引3边垂线后,2直角边都被分为2截,直角处和2条从圆心引得半径形成正方形,2直角边剩余线段的和刚好为斜边长度
所以周长=1+1+8+8=18
4.B
解析:
三角形的外接圆是三条垂直平分线的交点,有且只有一个交点,所以任意三角形一定有一个外接圆,并且只有一个外接圆,①是对的;
圆的内接三角形可以无数多个,所以②是错的;
三角形的内切圆的圆心是三个内角平分线的交点,有且只有一个交点,所以任意一个三角形一定有一个内切圆,并且只有一个内切圆,③是对的;
圆的外切三角形可以有无数多个,④是错误的.
所以①③正确,正确的有2个.
故选B.
5.B
解析:
分析:根据切线的性质和∠P的度数得出△PAB为等边三角形,从而得出答案.
详解:∵PA和PB为切线, ∴PA=PB, ∵∠P=60°, ∴△PAB为等边三角形,
6.C
解析:设O分别与△ABC的BC边,AB的延长线,AC的延长线相切,切点分别为D,E,F,
∴OE⊥AB,OF⊥AC,
故选C.
7.B
解析:设分别是的切点,
是一张三角形的纸片, 是它的内切圆,点是其中的一个切点,
则
故
故选B.
8.B
解析:
如下图,连接AD,BD,
∵同弧所对的圆周角相等,∴∠ABD=∠AED=20°,
∵AB为直径,∴∠ADB=90°,
∴∠BAD=90°-20°=70°,
∴∠BCD=180°-70°=110°.
故选B
9.6
解析:
∵ △ABC的边与⊙O分别相切于点D,E,F,
∴BD=BE,CD=CF,AE=AF,
∴AB+AC+BC=AE+EB+BD+DC+CF+FA
=2AE+2DC+2BD
=2AE+10+6
=2AE+16
=22cm,
则AE=3cm,
∴AB=AE+BE=AE+BD=3+3=6cm.
故答案为:6.
10.52
解析:
根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=52
故填:52
11.4
解析:连接AO、OD;
∵O是△ABC的内心,
∴OA平分∠BAC,
∵⊙O是△ABC的内切圆,D是切点,
∴OD⊥BC;
又∵AC=AB,
∴A、O、D三点共线,即AD⊥BC,
∵CD、CE是⊙O的切线,
∴CD=CE=2,
在Rt△ACD中,由∠C=30°,CD=2,得
AC==4.
12.解析:(1)根据切线长定理,
知
(2)连接
在中,
∴圆的直径为
即只需测得的长,就可求得圆的直径.
点睛:切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.
13.AI=.
解析:
连结CI,BI,且延长BI交AC于点F,过点I作IG⊥BC于点G,IE⊥AB于点E.∵AB=BC=5,点I为△ABC的内心,∴BF⊥AC,AF=CF.在Rt△ABF中,
∵sin∠BAC=,∴BF=4.∴AF==3,∴AC=6.∵点I是△ABC的内心,IE⊥AB,IF⊥AC,IG⊥BC,∴IE=IF=IG.∴S△ABC=AB+AC+BC)·IF=AC·BF,∴IF=,∴AI==.
14.5
解析:
解:连接OC、OD.
∵OA是⊙B的直径,
∴∠OCA=∠ODA=90°,
∴AC、AD都是⊙O的切线.
∴AD=AC=5.
15.16cm.
解析:
解:∵PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
∴PA=PB,EA=EQ,FB=FQ,
∵PA=8cm,
∴△PEF的周长为:PE+EF+PF=PA+PB=8+8=16(cm)
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
