1.2 30,45,60角的三角函数值 同步练习(含详解)
文档属性
| 名称 | 1.2 30,45,60角的三角函数值 同步练习(含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 728.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
1.2 30,45,60角的三角函数值
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.锐角三角函数tan30°的值是( )
A.1 B. C. D.
2.已知在Rt△ABC中,∠C=90°,cosA=,则sinB的值是( )
A. B. C. D.
3.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.( ,1) B.(1, ) C.( +1,1) D.(1,+1)
4.如果∠α是等边三角形的一个内角,那么cosα的值等于(?? )
A. B. C. D.1
5.如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
B.2 C.2 D.4
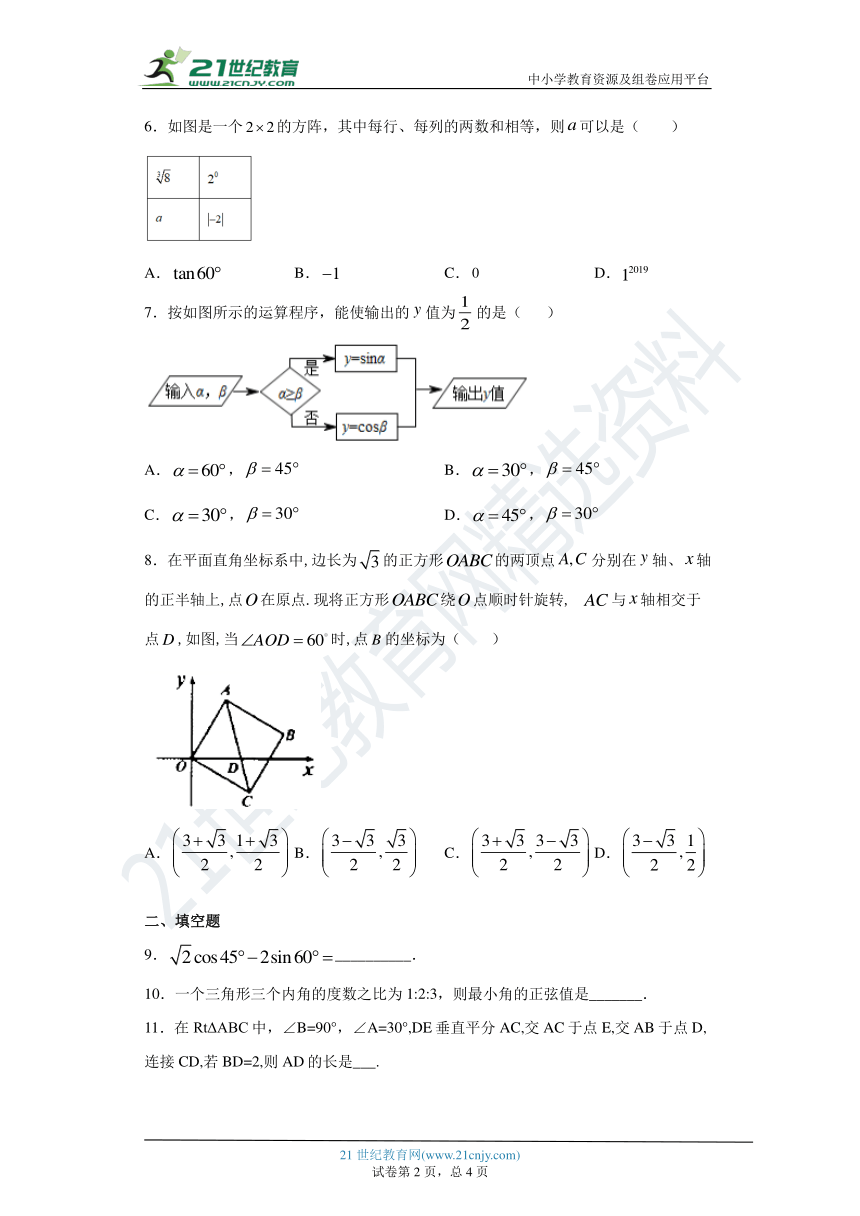
6.如图是一个的方阵,其中每行、每列的两数和相等,则可以是( )
A. B. C. D.
7.按如图所示的运算程序,能使输出的值为的是( )
A., B.,
C., D.,
8.在平面直角坐标系中,边长为的正方形的两顶点分别在轴、轴的正半轴上,点在原点.现将正方形绕点顺时针旋转, 与轴相交于点,如图,当时,点的坐标为( )
A. B. C. D.
二、填空题
9.__________.
10.一个三角形三个内角的度数之比为1:2:3,则最小角的正弦值是_______.
11.在RtΔABC中,∠B=90°,∠A=30°,DE垂直平分AC,交AC于点E,交AB于点D,连接CD,若BD=2,则AD的长是___.
12.如图,在中,于点,于点,,交于点,为的中点,连接,,,则下列结论:①;②;③;④若时,.其中正确的是________(把所有正确结论的序号都选上)
三、解答题
13.计算:
14.先化简,再求代数式的值,其中,.
15.如图,在△ABC中,,,将绕点逆时针旋转得到△A′BC′,连接,求的长.
16.如图,已知△ABC.
(1)尺规作图:作BC边上的高AD;(保留作图痕迹,不写作法)
(2)若∠B=45°,∠C=30°,AC=4,求AB的长.
参考答案
1.B
解析:
解:tan30°.
故选:B.
2.D
解析:
在Rt△ABC中,∠C=90°.
∵cosA,∴∠A=30°,∴∠B=60°,∴sinB=sin60°.
故选D.
3.C
解析:过点作 轴于点,
∵是菱形,
∴点的坐标为:
故选C.
4.A
解析:
解:∠α是等边三角形的一个内角,所以
故选: A
5.B
解析:
过点O作OD⊥BC于D,
则BC=2BD,
∵△ABC内接于⊙O,∠BAC与∠BOC互补,
∴∠BOC=2∠A,∠BOC+∠A=180°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBC=∠OCB=(180°?∠BOC)=30°,
∵⊙O的半径为2,
∴BD=OB·cos∠OBC=2×=,
∴BC=2.
故答案为2.
6.D
解析:由题意得:,
即:,解得:,
其中,
故选:D
7.C
解析:A. ,时,y=sin60°=,
B. ,时,y=cos45°=,
C. ,时,y=sin30°=,
D. ,时,y=cos45°=,
故选C.
8.C
解析:过点A作AE⊥x轴,作BF⊥AE,垂足分别是E,F.如图
∵∠AOD=60°,AE⊥OD
∴∠OAE=30°
∴OE=OA=,AE=OE=
∵∠OAE+∠AOE=90°,∠OAE+∠EAB=90°
∴∠AOE=∠AFB,且∠AEO=∠AFB=90°,OA=OB
∴△AOE≌△AFB(AAS)
∴AF=OE=,BF=AE=
∴EF=-
∴B
故选C.
9.
解析:
=
=
故答案为:.
10.
解析:设这三个内角分别为,,,
由题意得,,
解得:,
即最小角为30°,
最小角的正弦值是,
故答案为:.
11.4
解析:∵DE垂直平分AC,
∴AD=CD,
∴△ADC是等腰三角形,∠A=∠ACD=30°
又∵在RtΔABC中,∠B=90°,∠A=30°,
∴∠ACB=60°,∠BCD=30°
又∵BD=2,
∴sin∠BCD==
∴CD=4
∴AD=4.
故答案为4.
12.①②③④
解析:∵于点,于点
∴
∵为的中点
∴,
∴,选项①正确;
∵,
∴
∴,即
∴②正确;
∵
∴
又∵
∴
∴
∵,
∴
∵
∴
∴③正确;
∵,
∴
∵为的中点
∴
∴
∴④正确;
故答案为:①②③④.
13.
解析:
原式=.
14.
解析:
解:原式
,
∵,,
∴原式.
15..
解析:
解:如图,连接CC',
∵△ABC绕点B逆时针旋转60°得到△A′BC′,
∴BC=BC′=6,∠CBC′=60°,A′B=AB=AC=A′C′=5,
∴△BCC'是等边三角形,
∴BC=C'C,
∵A'B=A'C',
∴A'C是BC'的垂直平分线,垂足为D,
∴BD=BC'=3,
在Rt△A'BD中,A'B=5,BD=3,根据勾股定理得,A'D=4,
在Rt△BCD中,∠CBD=60°,BC=6,
∴CD=BC?cos∠CBD=6×sin60°=3,
∴A'C=A'D+CD=4+3.
16.
解析:
(1)如图所示,线段AD为所求;
(2)在Rt△ACD中,∵∠C=30°,
∴,
在Rt△ABD中,.
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
1.2 30,45,60角的三角函数值
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.锐角三角函数tan30°的值是( )
A.1 B. C. D.
2.已知在Rt△ABC中,∠C=90°,cosA=,则sinB的值是( )
A. B. C. D.
3.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.( ,1) B.(1, ) C.( +1,1) D.(1,+1)
4.如果∠α是等边三角形的一个内角,那么cosα的值等于(?? )
A. B. C. D.1
5.如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连结OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( )
B.2 C.2 D.4
6.如图是一个的方阵,其中每行、每列的两数和相等,则可以是( )
A. B. C. D.
7.按如图所示的运算程序,能使输出的值为的是( )
A., B.,
C., D.,
8.在平面直角坐标系中,边长为的正方形的两顶点分别在轴、轴的正半轴上,点在原点.现将正方形绕点顺时针旋转, 与轴相交于点,如图,当时,点的坐标为( )
A. B. C. D.
二、填空题
9.__________.
10.一个三角形三个内角的度数之比为1:2:3,则最小角的正弦值是_______.
11.在RtΔABC中,∠B=90°,∠A=30°,DE垂直平分AC,交AC于点E,交AB于点D,连接CD,若BD=2,则AD的长是___.
12.如图,在中,于点,于点,,交于点,为的中点,连接,,,则下列结论:①;②;③;④若时,.其中正确的是________(把所有正确结论的序号都选上)
三、解答题
13.计算:
14.先化简,再求代数式的值,其中,.
15.如图,在△ABC中,,,将绕点逆时针旋转得到△A′BC′,连接,求的长.
16.如图,已知△ABC.
(1)尺规作图:作BC边上的高AD;(保留作图痕迹,不写作法)
(2)若∠B=45°,∠C=30°,AC=4,求AB的长.
参考答案
1.B
解析:
解:tan30°.
故选:B.
2.D
解析:
在Rt△ABC中,∠C=90°.
∵cosA,∴∠A=30°,∴∠B=60°,∴sinB=sin60°.
故选D.
3.C
解析:过点作 轴于点,
∵是菱形,
∴点的坐标为:
故选C.
4.A
解析:
解:∠α是等边三角形的一个内角,所以
故选: A
5.B
解析:
过点O作OD⊥BC于D,
则BC=2BD,
∵△ABC内接于⊙O,∠BAC与∠BOC互补,
∴∠BOC=2∠A,∠BOC+∠A=180°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBC=∠OCB=(180°?∠BOC)=30°,
∵⊙O的半径为2,
∴BD=OB·cos∠OBC=2×=,
∴BC=2.
故答案为2.
6.D
解析:由题意得:,
即:,解得:,
其中,
故选:D
7.C
解析:A. ,时,y=sin60°=,
B. ,时,y=cos45°=,
C. ,时,y=sin30°=,
D. ,时,y=cos45°=,
故选C.
8.C
解析:过点A作AE⊥x轴,作BF⊥AE,垂足分别是E,F.如图
∵∠AOD=60°,AE⊥OD
∴∠OAE=30°
∴OE=OA=,AE=OE=
∵∠OAE+∠AOE=90°,∠OAE+∠EAB=90°
∴∠AOE=∠AFB,且∠AEO=∠AFB=90°,OA=OB
∴△AOE≌△AFB(AAS)
∴AF=OE=,BF=AE=
∴EF=-
∴B
故选C.
9.
解析:
=
=
故答案为:.
10.
解析:设这三个内角分别为,,,
由题意得,,
解得:,
即最小角为30°,
最小角的正弦值是,
故答案为:.
11.4
解析:∵DE垂直平分AC,
∴AD=CD,
∴△ADC是等腰三角形,∠A=∠ACD=30°
又∵在RtΔABC中,∠B=90°,∠A=30°,
∴∠ACB=60°,∠BCD=30°
又∵BD=2,
∴sin∠BCD==
∴CD=4
∴AD=4.
故答案为4.
12.①②③④
解析:∵于点,于点
∴
∵为的中点
∴,
∴,选项①正确;
∵,
∴
∴,即
∴②正确;
∵
∴
又∵
∴
∴
∵,
∴
∵
∴
∴③正确;
∵,
∴
∵为的中点
∴
∴
∴④正确;
故答案为:①②③④.
13.
解析:
原式=.
14.
解析:
解:原式
,
∵,,
∴原式.
15..
解析:
解:如图,连接CC',
∵△ABC绕点B逆时针旋转60°得到△A′BC′,
∴BC=BC′=6,∠CBC′=60°,A′B=AB=AC=A′C′=5,
∴△BCC'是等边三角形,
∴BC=C'C,
∵A'B=A'C',
∴A'C是BC'的垂直平分线,垂足为D,
∴BD=BC'=3,
在Rt△A'BD中,A'B=5,BD=3,根据勾股定理得,A'D=4,
在Rt△BCD中,∠CBD=60°,BC=6,
∴CD=BC?cos∠CBD=6×sin60°=3,
∴A'C=A'D+CD=4+3.
16.
解析:
(1)如图所示,线段AD为所求;
(2)在Rt△ACD中,∵∠C=30°,
∴,
在Rt△ABD中,.
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
