1.1锐角三角函数 同步练习(含详解)
文档属性
| 名称 | 1.1锐角三角函数 同步练习(含详解) |

|
|
| 格式 | rar | ||
| 文件大小 | 724.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 11:06:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
1.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.中,,下列关系中正确的是( )
A. B. C. D.
2.在中,,于点D,下列式子表示B错误的是
A. B. C. D.
3.设为锐角,且,则tan( )
A. B. C. D.
4.若直角三角形两直角边长的比为,为较大锐角,则有( ).
A. B.
C. D.
5.在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为( )
A. B. C. D.
6.在离铁塔底部米的地面处测得铁塔塔顶的仰角为,那么铁塔的高为( )
A. B. C. D.
7.在Rt△ABC中,CD是斜边AB上的高,下列线段的比值不等于sinA的是:( )
A. B. C. D.
8.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD= ;③DF=DC;④△AEF∽△CAB;⑤S四边形CDEF=S△ABF ,其中正确的结论有(?? )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.用“”联结下列各题中的锐角、、.
(1)若,,,则、、的大小关系为______;
(2)若,,,则、、的大小关系为______.
10.在中,。
11.已知Rt△ABC中,∠C=90°,AC=3,∠B=37°,则BC的长为_____(注:tan∠B=0.75,sin∠B=0.6,cos∠B=0.8)
如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是 .
三、解答题
13.如图,已知数轴上点A表示的数为16,B是数轴上在A左侧的一点,且A,B两点间的距离为20.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动:
(1)数轴上点B表示的数是______;
(2)运动1秒时,点P表示的数是______;
(3)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,若点P、Q时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为5个单位长度?
14.已知为锐角,求满足下列条件的的度数(精确到1″,借助使用计算器).
(1);
(2);
(3);
(4).
15.如图,在Rt△ABC中,∠C=90°,D是BC边上一点,AC=2,CD=1,设∠CAD=α.
(1)求sinα、cosα、tanα的值;
(2)若∠B=∠CAD,求BD的长.
16.如图,在中,,于点D,,,设,求,,.
参考答案
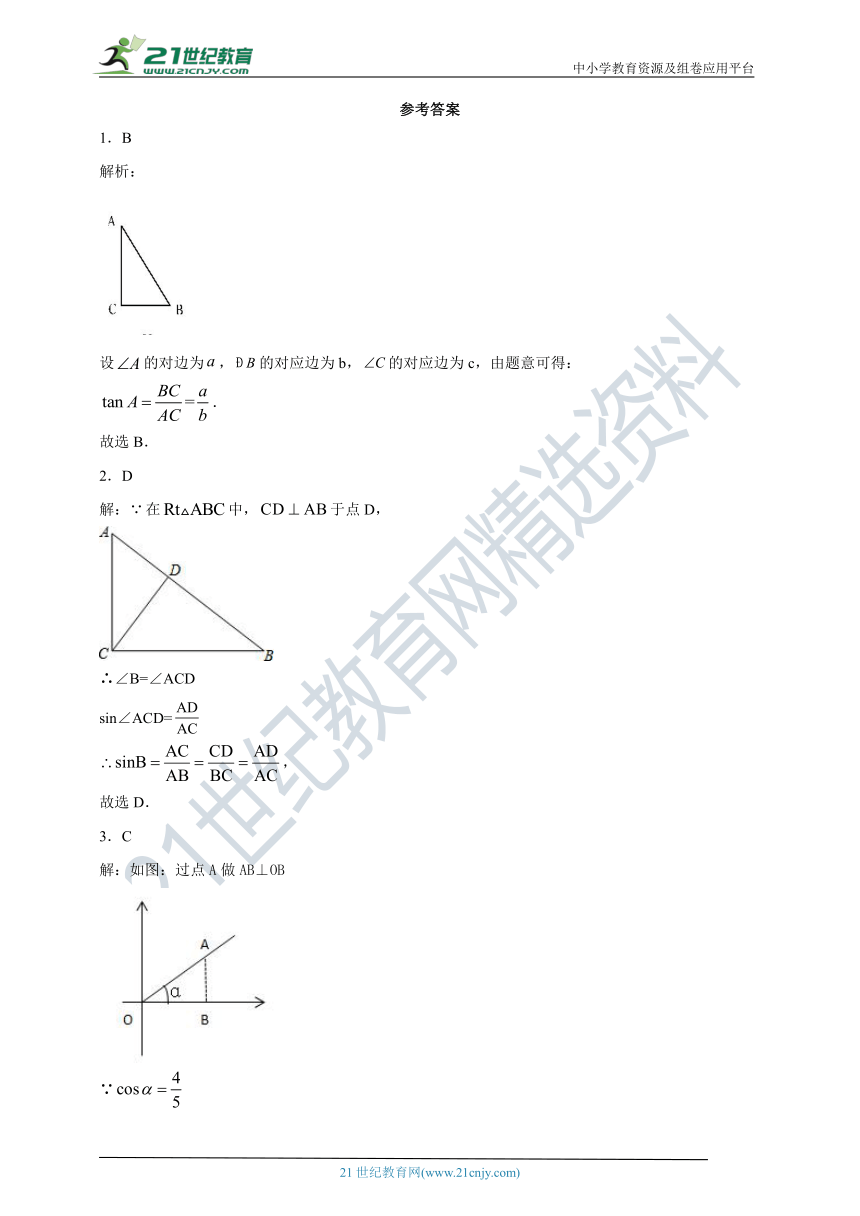
1.B
解析:
设的对边为,的对应边为b,的对应边为c,由题意可得:
.
故选B.
2.D
解析:
解:在中,于点D,
∴∠B=∠ACD
sin∠ACD=
,
故选D.
3.C
解析:
解:如图:过点A做AB⊥OB
∵
∴
设OB=4k,则OA=5k
根据勾股定理,
∴
故选:C.
4.C
解析:
∵为较大锐角,且两直角边长的比为,
∴tan=2,
故选C.
5.D
解析:
如图所示,∵∠C=90°,AC=12,BC=5,
∴,
∴.
6.C
解析:
解:如图所示:
由题意得,∠A=,AC=m,∠ACB=90°,
∴BC=ACtan∠A=ACtan=mtan.
故选C.
7.C
解析:
∵CD是斜边AB的高,
∴CD⊥AB,
∴∠A+∠ACD=90°,
又∵∠ACD+∠BCD=90°,
∴∠A=∠BCD,
A、在Rt△ABC中,sinA=,故本选项正确;
B、在Rt△ACD中,sinA=,故本选项正确;
C、在Rt△BCD中,sin∠BCD=,故本选项错误;
D、在Rt△BCD中,sin∠BCD==sinA,故本选项正确;
故选C.
8.D
解析:
解:∵AD∥BC,
∴△AEF∽△CBF,
∵AE= AD= BC,
∴CF=2AF,故①正确;
设AE=a,AB=b,则AD=2a,
∵BE⊥AC,∠BAD=90°,
∴∠ABE=∠ADC,而∠BAE=∠ADC=90°,
∴△BAE∽△ADC,
,即
,故②正确;
如图,过D作DM∥BE交AC于N,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE= BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故④正确;
如图,连接CE,
由△AEF∽△CBF,可得
设△AEF的面积为s,则△ABF的面积为2s,△CEF的面积为2s,
∴△ACE的面积为3s,
∵E是AD的中点,
∴△CDE的面积为3s,
∴四边形CDEF的面积为5s,
∴S四边形CDEF=S△ABF,故⑤正确.
故选:D.
9.
解析:
(1)∵,,
∴
∴
(2)∵,,
∴
∴
故答案为:;
10.6
解析:
∵,
∴AB===6.
故答案为6.
11.4
解析:
∵∠C=90°,∴tanB,∴BC4.
故答案为4.
12..
解析:
试题分析:根据翻转变换的性质得到∠AFE=∠D=90°,AF=AD=5,根据矩形的性质得到∠EFC=∠BAF,根据余弦的概念计算即可.
由翻转变换的性质可知,∠AFE=∠D=90°,AF=AD=5,
∴∠EFC+∠AFB=90°,∵∠B=90°,
∴∠BAF+∠AFB=90°,∴∠EFC=∠BAF,cos∠BAF==,
∴cos∠EFC=,故答案为.
考点:轴对称的性质,矩形的性质,余弦的概念.
13.(1)-4;(2)10;(3)①2秒;②1.5或2.5秒
解析:
解:(1)∵数轴上点A表示的数为16,B是数轴上在A左侧的一点,且A,B两点间的距离为20
∴点B表示的数为16-20=-4
故答案为:-4;
(2)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,运动1秒时,AP=1×6=6
∴点P表示的数是16-6=10
故答案为:10;
(3)①设当点P运动x秒时,点P与点Q相遇
由题意可得6x+4x=20
解得:x=2;
答:当点P运动2秒时,点P与点Q相遇;
②设当点P运动t秒时,点P与点Q间的距离为5个单位长度
当点P,Q相遇前,由题意可得6t+4t=20-5
解得:t=1.5;
当点P,Q相遇后,由题意可得6t+4t=20+5
解得:t=2.5;
答:当点P运动1.5或2.5秒时,点P与点Q间的距离为5个单位长度.
14.(1);(2);(3);(4).
解析:
解:(1)∵,
∴;
(2)∵,
∴;
(3)∵,
∴;
(4)∵,
∴.
15.(1)sinα=,cosα=,tanα=;(2)BD =3.
解析:
解:在Rt△ACD中,
∵AC=2,DC=1,
∴AD==.
(1)sinα===,cosα===,tanα==;
(2)在Rt△ABC中,
tanB=,
即tanα==,
∴BC=4,
∴BD=BC-CD=4-1=3.
16.,,
解析:
解:∵,
∴.
∵,
∴.
∴.
在中,,
∴,
∴,,.
∴,,.
故答案为:,,
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
1.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.中,,下列关系中正确的是( )
A. B. C. D.
2.在中,,于点D,下列式子表示B错误的是
A. B. C. D.
3.设为锐角,且,则tan( )
A. B. C. D.
4.若直角三角形两直角边长的比为,为较大锐角,则有( ).
A. B.
C. D.
5.在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为( )
A. B. C. D.
6.在离铁塔底部米的地面处测得铁塔塔顶的仰角为,那么铁塔的高为( )
A. B. C. D.
7.在Rt△ABC中,CD是斜边AB上的高,下列线段的比值不等于sinA的是:( )
A. B. C. D.
8.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD= ;③DF=DC;④△AEF∽△CAB;⑤S四边形CDEF=S△ABF ,其中正确的结论有(?? )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.用“”联结下列各题中的锐角、、.
(1)若,,,则、、的大小关系为______;
(2)若,,,则、、的大小关系为______.
10.在中,。
11.已知Rt△ABC中,∠C=90°,AC=3,∠B=37°,则BC的长为_____(注:tan∠B=0.75,sin∠B=0.6,cos∠B=0.8)
如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是 .
三、解答题
13.如图,已知数轴上点A表示的数为16,B是数轴上在A左侧的一点,且A,B两点间的距离为20.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动:
(1)数轴上点B表示的数是______;
(2)运动1秒时,点P表示的数是______;
(3)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,若点P、Q时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为5个单位长度?
14.已知为锐角,求满足下列条件的的度数(精确到1″,借助使用计算器).
(1);
(2);
(3);
(4).
15.如图,在Rt△ABC中,∠C=90°,D是BC边上一点,AC=2,CD=1,设∠CAD=α.
(1)求sinα、cosα、tanα的值;
(2)若∠B=∠CAD,求BD的长.
16.如图,在中,,于点D,,,设,求,,.
参考答案
1.B
解析:
设的对边为,的对应边为b,的对应边为c,由题意可得:
.
故选B.
2.D
解析:
解:在中,于点D,
∴∠B=∠ACD
sin∠ACD=
,
故选D.
3.C
解析:
解:如图:过点A做AB⊥OB
∵
∴
设OB=4k,则OA=5k
根据勾股定理,
∴
故选:C.
4.C
解析:
∵为较大锐角,且两直角边长的比为,
∴tan=2,
故选C.
5.D
解析:
如图所示,∵∠C=90°,AC=12,BC=5,
∴,
∴.
6.C
解析:
解:如图所示:
由题意得,∠A=,AC=m,∠ACB=90°,
∴BC=ACtan∠A=ACtan=mtan.
故选C.
7.C
解析:
∵CD是斜边AB的高,
∴CD⊥AB,
∴∠A+∠ACD=90°,
又∵∠ACD+∠BCD=90°,
∴∠A=∠BCD,
A、在Rt△ABC中,sinA=,故本选项正确;
B、在Rt△ACD中,sinA=,故本选项正确;
C、在Rt△BCD中,sin∠BCD=,故本选项错误;
D、在Rt△BCD中,sin∠BCD==sinA,故本选项正确;
故选C.
8.D
解析:
解:∵AD∥BC,
∴△AEF∽△CBF,
∵AE= AD= BC,
∴CF=2AF,故①正确;
设AE=a,AB=b,则AD=2a,
∵BE⊥AC,∠BAD=90°,
∴∠ABE=∠ADC,而∠BAE=∠ADC=90°,
∴△BAE∽△ADC,
,即
,故②正确;
如图,过D作DM∥BE交AC于N,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE= BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故④正确;
如图,连接CE,
由△AEF∽△CBF,可得
设△AEF的面积为s,则△ABF的面积为2s,△CEF的面积为2s,
∴△ACE的面积为3s,
∵E是AD的中点,
∴△CDE的面积为3s,
∴四边形CDEF的面积为5s,
∴S四边形CDEF=S△ABF,故⑤正确.
故选:D.
9.
解析:
(1)∵,,
∴
∴
(2)∵,,
∴
∴
故答案为:;
10.6
解析:
∵,
∴AB===6.
故答案为6.
11.4
解析:
∵∠C=90°,∴tanB,∴BC4.
故答案为4.
12..
解析:
试题分析:根据翻转变换的性质得到∠AFE=∠D=90°,AF=AD=5,根据矩形的性质得到∠EFC=∠BAF,根据余弦的概念计算即可.
由翻转变换的性质可知,∠AFE=∠D=90°,AF=AD=5,
∴∠EFC+∠AFB=90°,∵∠B=90°,
∴∠BAF+∠AFB=90°,∴∠EFC=∠BAF,cos∠BAF==,
∴cos∠EFC=,故答案为.
考点:轴对称的性质,矩形的性质,余弦的概念.
13.(1)-4;(2)10;(3)①2秒;②1.5或2.5秒
解析:
解:(1)∵数轴上点A表示的数为16,B是数轴上在A左侧的一点,且A,B两点间的距离为20
∴点B表示的数为16-20=-4
故答案为:-4;
(2)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,运动1秒时,AP=1×6=6
∴点P表示的数是16-6=10
故答案为:10;
(3)①设当点P运动x秒时,点P与点Q相遇
由题意可得6x+4x=20
解得:x=2;
答:当点P运动2秒时,点P与点Q相遇;
②设当点P运动t秒时,点P与点Q间的距离为5个单位长度
当点P,Q相遇前,由题意可得6t+4t=20-5
解得:t=1.5;
当点P,Q相遇后,由题意可得6t+4t=20+5
解得:t=2.5;
答:当点P运动1.5或2.5秒时,点P与点Q间的距离为5个单位长度.
14.(1);(2);(3);(4).
解析:
解:(1)∵,
∴;
(2)∵,
∴;
(3)∵,
∴;
(4)∵,
∴.
15.(1)sinα=,cosα=,tanα=;(2)BD =3.
解析:
解:在Rt△ACD中,
∵AC=2,DC=1,
∴AD==.
(1)sinα===,cosα===,tanα==;
(2)在Rt△ABC中,
tanB=,
即tanα==,
∴BC=4,
∴BD=BC-CD=4-1=3.
16.,,
解析:
解:∵,
∴.
∵,
∴.
∴.
在中,,
∴,
∴,,.
∴,,.
故答案为:,,
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
_21?????????è?????(www.21cnjy.com)_
