1.4解直角三角形 同步练习(含详解)
文档属性
| 名称 | 1.4解直角三角形 同步练习(含详解) | 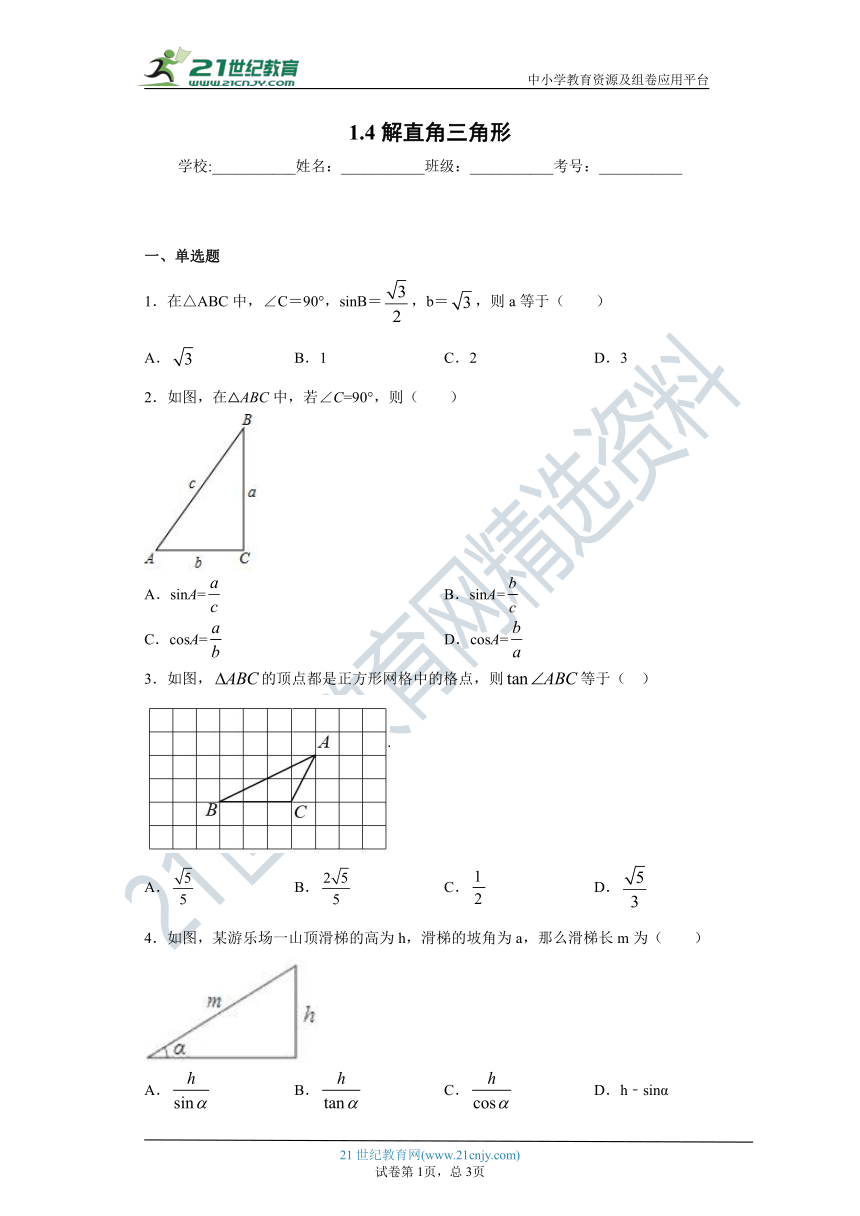 | |
| 格式 | doc | ||
| 文件大小 | 605.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 11:52:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
1.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,∠C=90°,sinB=,b=,则a等于( )
A. B.1 C.2 D.3
2.如图,在△ABC中,若∠C=90°,则( )
A.sinA= B.sinA=
C.cosA= D.cosA=
3.如图,的顶点都是正方形网格中的格点,则等于( )
A. B. C. D.
4.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
A. B. C. D.h﹣sinα
5.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
A.sinA= B.tanA= C.cosB= D.tanB=
6.a,b,c是中,,所对的边,且,则的值为( )
A. B. C. D.
7.在中,,,则( )
A. B. C. D.
8.如图,梯形护坡石坝的斜坡AB的坡度,坝高BC为2m,则斜坡AB的长是( )
A.m B.m C.m D.6m
二、填空题
9.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=,则菱形ABCD的周长是_____.
10.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .
11.在中,,,,则________,________,________.
12.一船上午8点位于灯塔A的北偏东60°方向,在与灯塔A相距64海里的B港出发,向正西方向航行,到9时30分恰好在灯塔正北的C处,则此船的速度为______.
三、解答题
13.已知中,,,,解这个直角三角形.
14.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
15.如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:(1)点B的坐标;(2)cos∠BAO的值.
16.矩形ABCD中,AB=AE=5,AD=3,求.
参考答案
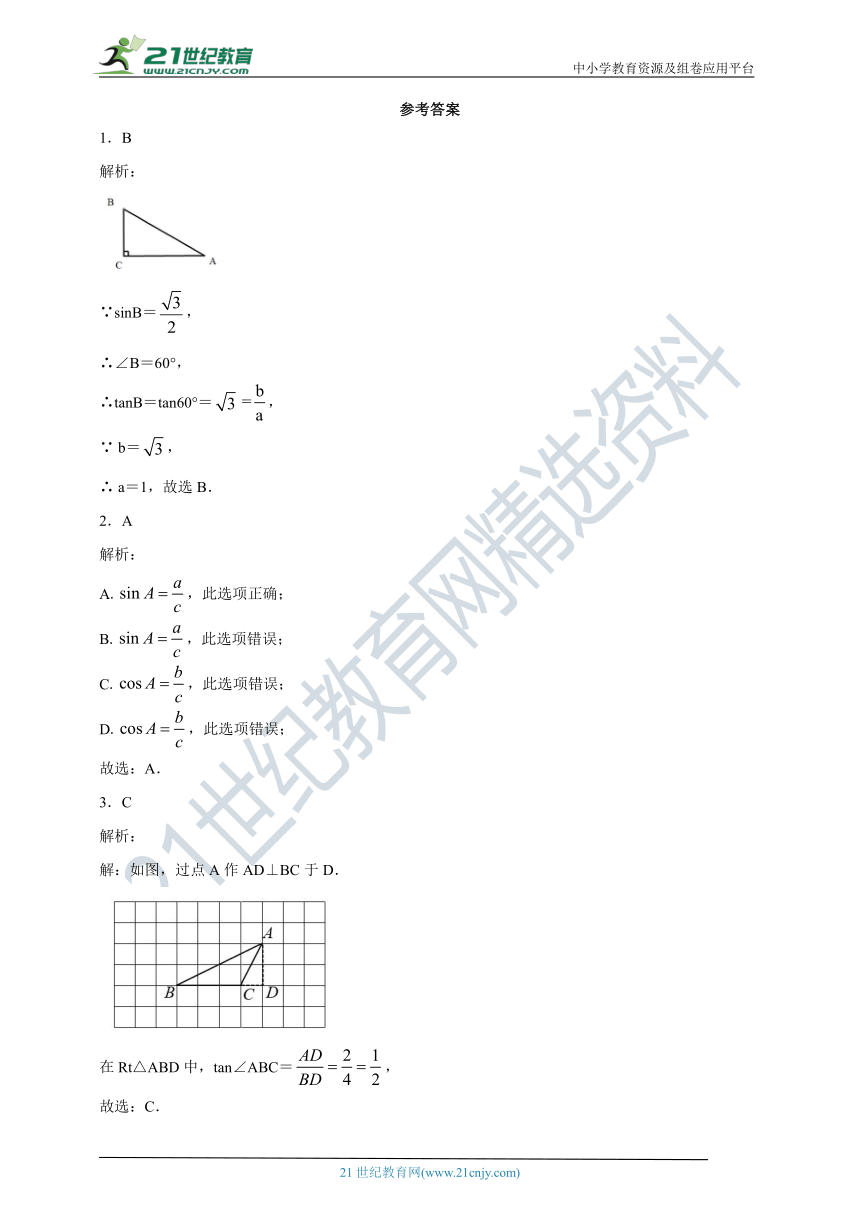
1.B
解析:
∵sinB=,
∴∠B=60°,
∴tanB=tan60°=,
∵ b=,
∴ a=1,故选B.
2.A
解析:
A.,此选项正确;
B.,此选项错误;
C.,此选项错误;
D.,此选项错误;
故选:A.
3.C
解析:
解:如图,过点A作AD⊥BC于D.
在Rt△ABD中,tan∠ABC=,
故选:C.
4.A
解析:
∵,
∴
故选:A.
5.D
解析:
解:∵在Rt△ABC中,∠ACB=90°,BC=1,AB=2.
∴AC=,
∴sinA=,tanA=,cosB=,tanB=.
故选:D.
6.B
解析:
解:∵
∴设
∵
∴是直角三角形
∴
故答案为:B
7.D
解析:
解:设BC=1
∵在中,,
∴
∴AC=3
由勾股定理得:
∴
故答案为D
8.B
解析:
∵斜坡AB的坡度,坝高BC为2m,
∴1:3=2:AC,
∴AC=6m,
由勾股定理得
AB=m.
故选B.
9.40
解析:
∵DE⊥AB,
∴△ADE是直角三角形,
∴,
∴AD=10,
∵菱形四个边是相等的,
∴菱形ABCD的周长=10×4=40.
10.105°.
解析:
连接OQ,
∵AC=BC,∠ACB=90°,
∴∠BAC=∠B=45°,
由旋转的性质可知:△AQC≌△BOC,
∴AQ=BO,CQ=CO,∠QAC=∠B=45°,∠ACQ=∠BCO,
∴∠OAQ=∠BAC+∠CAQ=90°,∠OCQ=∠OCA+∠ACQ=∠OCA+∠BCO=90°,
∴∠OQC=45°,
∵BO:OA=1:,
设BO=1,OA=,
∴AQ=1,则tan∠AQO==,
∴∠AQO=60°,
∴∠AQC=105°.
故答案为105°.
11.
解析:
解:根据勾股定理得:;
∴
故答案为:(1) (2) (3)
12.海里/时
解析:
∵AB=64,∠CAB=60°,
∴BC=AB?sin60°=32.
∵从B到C用时9.5-8=1.5时,
∴速度为32÷1.5=(海里/时).
故答案为:海里/时.
13.∠A=30°,BC=3,AC=.
解析:
解:在中,,,,
,
,
.
故答案为∠A=30°,BC=3,AC= .
14.sinA=,cosA=,tanA=.
解析:
由勾股定理得,,
则,,.
15.(1);(2).
解析:
解: (1)如图所示,作BH⊥OA, 垂足为H.
在Rt△OHB中,∵BO=5,sin∠BOA=,
∴BH=3,∴OH=4,
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,
∴AH=6.
在Rt△AHB中,
∵BH=3,
∴AB=,
∴cos∠BAO== .
16.3
解析:
∵矩形ABCD
∴DC∥AB,AD=BC,DC=AB,∠D=∠C=90°,
∴∠ABE=∠CEB,
∵AB=AE=5,AD=3
∴∠ABE=∠AEB,由勾股定理得DE= = 4
∴CE=DC-DE=5-4=1
∴
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
1.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,∠C=90°,sinB=,b=,则a等于( )
A. B.1 C.2 D.3
2.如图,在△ABC中,若∠C=90°,则( )
A.sinA= B.sinA=
C.cosA= D.cosA=
3.如图,的顶点都是正方形网格中的格点,则等于( )
A. B. C. D.
4.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
A. B. C. D.h﹣sinα
5.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
A.sinA= B.tanA= C.cosB= D.tanB=
6.a,b,c是中,,所对的边,且,则的值为( )
A. B. C. D.
7.在中,,,则( )
A. B. C. D.
8.如图,梯形护坡石坝的斜坡AB的坡度,坝高BC为2m,则斜坡AB的长是( )
A.m B.m C.m D.6m
二、填空题
9.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=,则菱形ABCD的周长是_____.
10.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .
11.在中,,,,则________,________,________.
12.一船上午8点位于灯塔A的北偏东60°方向,在与灯塔A相距64海里的B港出发,向正西方向航行,到9时30分恰好在灯塔正北的C处,则此船的速度为______.
三、解答题
13.已知中,,,,解这个直角三角形.
14.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
15.如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:(1)点B的坐标;(2)cos∠BAO的值.
16.矩形ABCD中,AB=AE=5,AD=3,求.
参考答案
1.B
解析:
∵sinB=,
∴∠B=60°,
∴tanB=tan60°=,
∵ b=,
∴ a=1,故选B.
2.A
解析:
A.,此选项正确;
B.,此选项错误;
C.,此选项错误;
D.,此选项错误;
故选:A.
3.C
解析:
解:如图,过点A作AD⊥BC于D.
在Rt△ABD中,tan∠ABC=,
故选:C.
4.A
解析:
∵,
∴
故选:A.
5.D
解析:
解:∵在Rt△ABC中,∠ACB=90°,BC=1,AB=2.
∴AC=,
∴sinA=,tanA=,cosB=,tanB=.
故选:D.
6.B
解析:
解:∵
∴设
∵
∴是直角三角形
∴
故答案为:B
7.D
解析:
解:设BC=1
∵在中,,
∴
∴AC=3
由勾股定理得:
∴
故答案为D
8.B
解析:
∵斜坡AB的坡度,坝高BC为2m,
∴1:3=2:AC,
∴AC=6m,
由勾股定理得
AB=m.
故选B.
9.40
解析:
∵DE⊥AB,
∴△ADE是直角三角形,
∴,
∴AD=10,
∵菱形四个边是相等的,
∴菱形ABCD的周长=10×4=40.
10.105°.
解析:
连接OQ,
∵AC=BC,∠ACB=90°,
∴∠BAC=∠B=45°,
由旋转的性质可知:△AQC≌△BOC,
∴AQ=BO,CQ=CO,∠QAC=∠B=45°,∠ACQ=∠BCO,
∴∠OAQ=∠BAC+∠CAQ=90°,∠OCQ=∠OCA+∠ACQ=∠OCA+∠BCO=90°,
∴∠OQC=45°,
∵BO:OA=1:,
设BO=1,OA=,
∴AQ=1,则tan∠AQO==,
∴∠AQO=60°,
∴∠AQC=105°.
故答案为105°.
11.
解析:
解:根据勾股定理得:;
∴
故答案为:(1) (2) (3)
12.海里/时
解析:
∵AB=64,∠CAB=60°,
∴BC=AB?sin60°=32.
∵从B到C用时9.5-8=1.5时,
∴速度为32÷1.5=(海里/时).
故答案为:海里/时.
13.∠A=30°,BC=3,AC=.
解析:
解:在中,,,,
,
,
.
故答案为∠A=30°,BC=3,AC= .
14.sinA=,cosA=,tanA=.
解析:
由勾股定理得,,
则,,.
15.(1);(2).
解析:
解: (1)如图所示,作BH⊥OA, 垂足为H.
在Rt△OHB中,∵BO=5,sin∠BOA=,
∴BH=3,∴OH=4,
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,
∴AH=6.
在Rt△AHB中,
∵BH=3,
∴AB=,
∴cos∠BAO== .
16.3
解析:
∵矩形ABCD
∴DC∥AB,AD=BC,DC=AB,∠D=∠C=90°,
∴∠ABE=∠CEB,
∵AB=AE=5,AD=3
∴∠ABE=∠AEB,由勾股定理得DE= = 4
∴CE=DC-DE=5-4=1
∴
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
