人教版九年级数学下册 第27章 相似 27.2.2用平行线判定三角形相似 习题课件(共24张ppt)
文档属性
| 名称 | 人教版九年级数学下册 第27章 相似 27.2.2用平行线判定三角形相似 习题课件(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 855.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 21:37:54 | ||
图片预览






文档简介
(共24张PPT)
人教版九年级数学下册
第27章
相似
27.2
相似三角形
第2课时
用平行线判定三角形相似
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
C
B
D
C
C
8
B
B
C
提示:点击
进入习题
答案显示
10
11
12
9
见习题
见习题
B
见习题
13
见习题
1.如图,在△ABC中,DE∥BC,GF∥AC,GF,DE相交于M点,则图中与△ABC相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
C
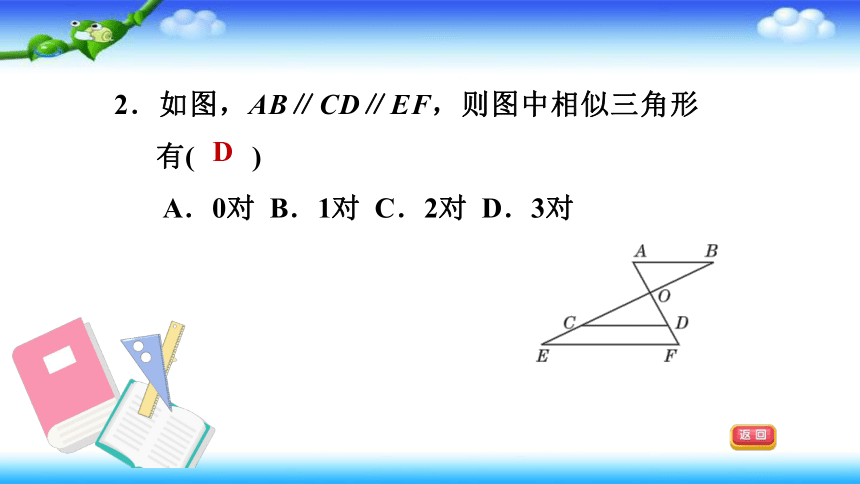
2.如图,AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.1对
C.2对
D.3对
D
3.如图,在?ABCD中,过点B的直线与对角线AC,边AD分别交于点E和点F,过点E作EG∥BC,交AB于点G,则图中相似三角形有( )
A.4对
B.5对
C.6对
D.7对
B
【点拨】图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA,共5对.
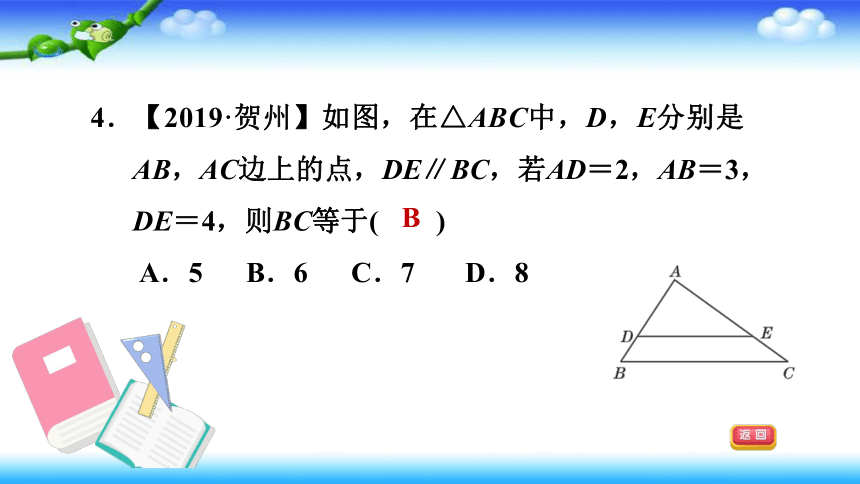
4.【2019·贺州】如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )
A.5
B.6
C.7
D.8
B
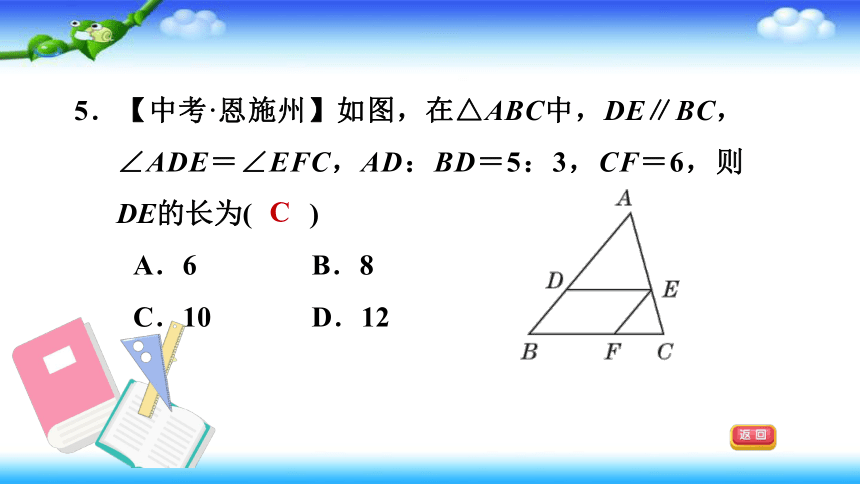
5.【中考·恩施州】如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A.6
B.8
C.10
D.12
C
C
C
8.【2019·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6
B.4
C.4.8
D.5
【答案】B
9.【中考·恩施州】如图,在?ABCD中,EF∥AB交BD于F,交AD于E.DE:EA=3:4,EF=3,则CD的长是( )
A.4
B.7
C.3
D.12
B
10.【2019·张家界】如图,在?ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC于点F,G.
(1)求证:BF=CF;
(2)若DG=4,求FG的长.
11.如图,已知EC∥AB,∠EDA=∠ABF.求证:
(1)四边形ABCD是平行四边形;
证明:∵EC∥AB,∴∠EDA=∠DAB.
∵∠EDA=∠ABF,∴∠DAB=∠ABF.
∴AD∥BC.
∵DC∥AB,∴四边形ABCD是平行四边形.
(2)OA2=OE·OF.
12.【2020·天门】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.
(1)求证:DF是⊙O的切线;
证明:如图,连接OD,AD.∵AB是直径,
∴∠ADB=90°.∴AD⊥BC.
∵AB=AC,∴∠BAC=2∠BAD.
∵∠BAC=2∠BDE,∴∠BDE=∠BAD.
∵OA=OD,∴∠BAD=∠ADO.
∵∠ADO+∠ODB=90°,∴∠BDE+∠ODB=90°.
∴∠ODE=90°,即DF⊥OD.
又∵OD是⊙O的半径,∴DF是⊙O的切线.
(2)当CF=2,BE=3时,求AF的长.
13.【2019·黄冈】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE.求证:
(1)△DBE是等腰三角形;
证明:连接OD,如图所示.
∵DE是⊙O的切线,∴∠ODE=90°.
∴∠ADO+∠BDE=90°.
∵∠ACB=90°,∴∠A+∠B=90°.
∵OA=OD,∴∠A=∠ADO.
∴∠BDE=∠B.∴EB=ED.
∴△DBE是等腰三角形.
(2)△COE∽△CAB.
解:∵∠ACB=90°,AC是⊙O的直径,
∴CB是⊙O的切线.
∵DE是⊙O的切线,∴ED=EC.
∵EB=ED,∴EC=EB.
又∵OA=OC,∴OE∥AB.
∴△COE∽△CAB.
谢谢欣赏
THANK
YOU
FOR
LISTENING
人教版九年级数学下册
第27章
相似
27.2
相似三角形
第2课时
用平行线判定三角形相似
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
C
B
D
C
C
8
B
B
C
提示:点击
进入习题
答案显示
10
11
12
9
见习题
见习题
B
见习题
13
见习题
1.如图,在△ABC中,DE∥BC,GF∥AC,GF,DE相交于M点,则图中与△ABC相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
C
2.如图,AB∥CD∥EF,则图中相似三角形有( )
A.0对
B.1对
C.2对
D.3对
D
3.如图,在?ABCD中,过点B的直线与对角线AC,边AD分别交于点E和点F,过点E作EG∥BC,交AB于点G,则图中相似三角形有( )
A.4对
B.5对
C.6对
D.7对
B
【点拨】图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA,共5对.
4.【2019·贺州】如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )
A.5
B.6
C.7
D.8
B
5.【中考·恩施州】如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A.6
B.8
C.10
D.12
C
C
C
8.【2019·安徽】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为( )
A.3.6
B.4
C.4.8
D.5
【答案】B
9.【中考·恩施州】如图,在?ABCD中,EF∥AB交BD于F,交AD于E.DE:EA=3:4,EF=3,则CD的长是( )
A.4
B.7
C.3
D.12
B
10.【2019·张家界】如图,在?ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC于点F,G.
(1)求证:BF=CF;
(2)若DG=4,求FG的长.
11.如图,已知EC∥AB,∠EDA=∠ABF.求证:
(1)四边形ABCD是平行四边形;
证明:∵EC∥AB,∴∠EDA=∠DAB.
∵∠EDA=∠ABF,∴∠DAB=∠ABF.
∴AD∥BC.
∵DC∥AB,∴四边形ABCD是平行四边形.
(2)OA2=OE·OF.
12.【2020·天门】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.
(1)求证:DF是⊙O的切线;
证明:如图,连接OD,AD.∵AB是直径,
∴∠ADB=90°.∴AD⊥BC.
∵AB=AC,∴∠BAC=2∠BAD.
∵∠BAC=2∠BDE,∴∠BDE=∠BAD.
∵OA=OD,∴∠BAD=∠ADO.
∵∠ADO+∠ODB=90°,∴∠BDE+∠ODB=90°.
∴∠ODE=90°,即DF⊥OD.
又∵OD是⊙O的半径,∴DF是⊙O的切线.
(2)当CF=2,BE=3时,求AF的长.
13.【2019·黄冈】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE.求证:
(1)△DBE是等腰三角形;
证明:连接OD,如图所示.
∵DE是⊙O的切线,∴∠ODE=90°.
∴∠ADO+∠BDE=90°.
∵∠ACB=90°,∴∠A+∠B=90°.
∵OA=OD,∴∠A=∠ADO.
∴∠BDE=∠B.∴EB=ED.
∴△DBE是等腰三角形.
(2)△COE∽△CAB.
解:∵∠ACB=90°,AC是⊙O的直径,
∴CB是⊙O的切线.
∵DE是⊙O的切线,∴ED=EC.
∵EB=ED,∴EC=EB.
又∵OA=OC,∴OE∥AB.
∴△COE∽△CAB.
谢谢欣赏
THANK
YOU
FOR
LISTENING
