人教版九年级数学下册 第27章 相似 27.2.3用三边比例关系判定三角形相似 习题课件(共23张ppt)
文档属性
| 名称 | 人教版九年级数学下册 第27章 相似 27.2.3用三边比例关系判定三角形相似 习题课件(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 859.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 21:33:32 | ||
图片预览








文档简介
(共23张PPT)
人教版九年级数学下册
第27章
相似
27.2
相似三角形
第3课时
用三边比例关系判定三角形相似
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
B
D
C
B
B
8
B
B
B
提示:点击
进入习题
答案显示
10
11
12
9
见习题
见习题
见习题
见习题
1.已知△ABC的三边长分别为2,5,6.若要使△DEF∽△ABC,则△DEF的三边长可以是( )
A.3,6,7
B.6,15,18
C.3,8,9
D.8,10,12
B
2.已知△ABC的三边长分别为6
cm,7.5
cm,9
cm,△DEF的一边长为4
cm,当△DEF的另两边长是下列( )组时,这两个三角形相似.
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
C
【答案】
D
【点拨】紧扣相似三角形对应点的不确定性,应分情况讨论,分别求出另外两边的长.
B
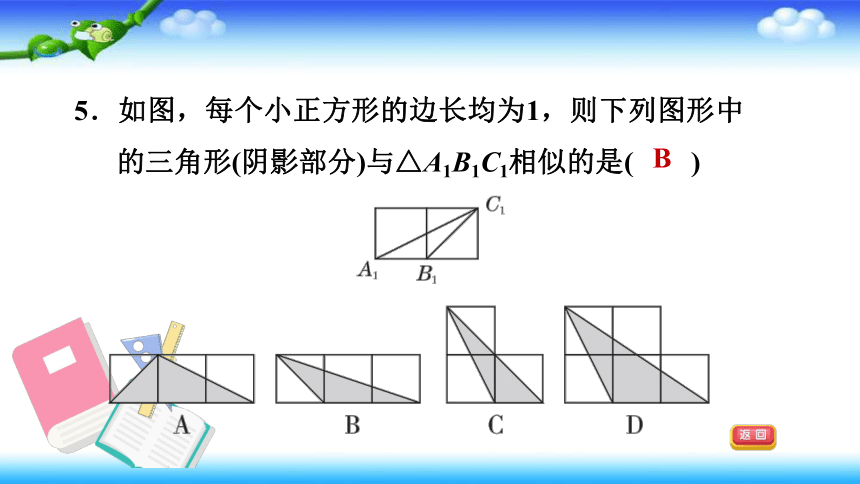
5.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
B
6.如图,在由相同的小正方形组成的网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.②~⑥中与①相似的是( )
A.②③④
B.③④⑤
C.④⑤⑥
D.②③⑥
B
7.【2019·连云港】在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似( )
A.①处
B.②处
C.③处
D.④处
【答案】B
8.【中考·东营】如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的边长分别是3,4及x,那么x的值( )
A.只有1个
B.可以有2个
C.可以有3个
D.有无数个
B
9.如图,O为△ABC内一点,点D,E,F分别是OA,OB,OC的中点,求证:△DEF∽△ABC.
10.(1)根据下面条件,判断△ABC与△A′B′C′是否相似,并说明理由;
AB=4
cm,BC=6
cm,AC=8
cm.
A′B′=12
cm,B′C′=18
cm,A′C′=21
cm.
(2)若(1)中两三角形不相似,那么要使它们相似,不改变AC的长,A′C′的长应改为多少?
解:当A′C′=24
cm时,两三角形相似.
11.如图,四边形ABCD,CDEF,EFGH都是边长相等的正方形.
(1)△ACF与△GCA相似吗?说说你的理由.
(2)求∠1+∠2的度数.
解:∵△ACF∽△GCA,∴∠1=∠CAF.
∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
12.【中考·菏泽】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画1个三角形,使它的3个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似,并予以证明.
谢谢欣赏
THANK
YOU
FOR
LISTENING
人教版九年级数学下册
第27章
相似
27.2
相似三角形
第3课时
用三边比例关系判定三角形相似
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
B
D
C
B
B
8
B
B
B
提示:点击
进入习题
答案显示
10
11
12
9
见习题
见习题
见习题
见习题
1.已知△ABC的三边长分别为2,5,6.若要使△DEF∽△ABC,则△DEF的三边长可以是( )
A.3,6,7
B.6,15,18
C.3,8,9
D.8,10,12
B
2.已知△ABC的三边长分别为6
cm,7.5
cm,9
cm,△DEF的一边长为4
cm,当△DEF的另两边长是下列( )组时,这两个三角形相似.
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
C
【答案】
D
【点拨】紧扣相似三角形对应点的不确定性,应分情况讨论,分别求出另外两边的长.
B
5.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
B
6.如图,在由相同的小正方形组成的网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.②~⑥中与①相似的是( )
A.②③④
B.③④⑤
C.④⑤⑥
D.②③⑥
B
7.【2019·连云港】在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似( )
A.①处
B.②处
C.③处
D.④处
【答案】B
8.【中考·东营】如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的边长分别是3,4及x,那么x的值( )
A.只有1个
B.可以有2个
C.可以有3个
D.有无数个
B
9.如图,O为△ABC内一点,点D,E,F分别是OA,OB,OC的中点,求证:△DEF∽△ABC.
10.(1)根据下面条件,判断△ABC与△A′B′C′是否相似,并说明理由;
AB=4
cm,BC=6
cm,AC=8
cm.
A′B′=12
cm,B′C′=18
cm,A′C′=21
cm.
(2)若(1)中两三角形不相似,那么要使它们相似,不改变AC的长,A′C′的长应改为多少?
解:当A′C′=24
cm时,两三角形相似.
11.如图,四边形ABCD,CDEF,EFGH都是边长相等的正方形.
(1)△ACF与△GCA相似吗?说说你的理由.
(2)求∠1+∠2的度数.
解:∵△ACF∽△GCA,∴∠1=∠CAF.
∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
12.【中考·菏泽】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画1个三角形,使它的3个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似,并予以证明.
谢谢欣赏
THANK
YOU
FOR
LISTENING
