6.4探索三角形相似的条件课后练习(含解析)
文档属性
| 名称 | 6.4探索三角形相似的条件课后练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 06:57:22 | ||
图片预览



文档简介
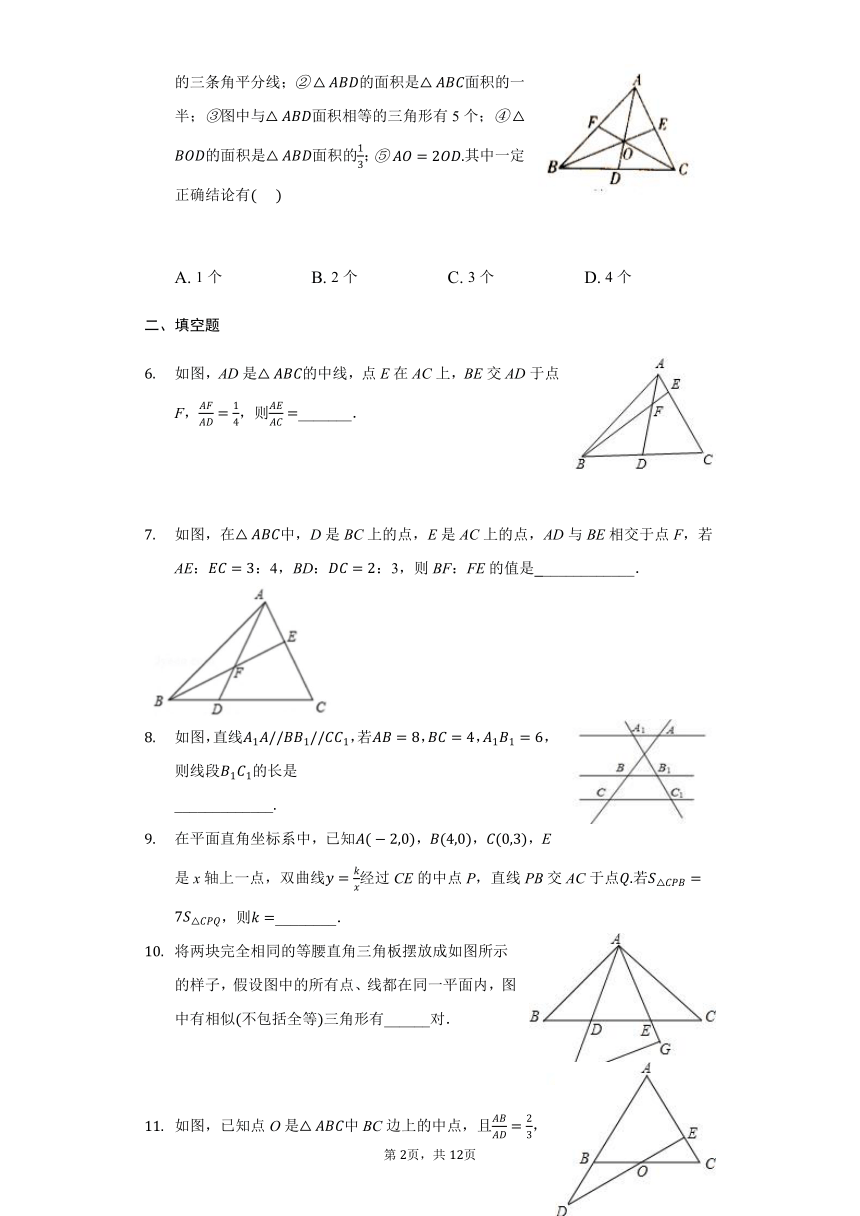
2020九下6.4探索三角形相似的条件课后练习
班级:___________姓名:___________得分:___________
一、选择题
如图,AB为的直径,C为上一点,弦AD平分,交BC于点E,,,则DE的长为
A.
B.
C.
2
D.
在中,点D,E,F分别在边AB,AC,BC上,若,,则下面所列比例式中正确的是
A.
B.
C.
D.
如图,在四边形ABCD中,,且AC与BD相交于点O,过点O作,分别交AB,CD于E,F,则图中相似的三角形共有【】
A.
6对
B.
5对
C.
4对
D.
3对
如图,在四边形ABCD中,,,,,点M为BC上异于B、C的一定点,点N为AB上的一动点,E、F分别为DM、MN的中点,当N从A到B的运动过程中,线段EF扫过图形的面积为
A.
4
B.
C.
5
D.
6
如图,在中,点F,D,E分别是边AB,BC,AC上的点,且AD,BE,CF相交于点O,若点O是的重心则以下结论:线段AD,BE,CF是的三条角平分线;的面积是面积的一半;图中与面积相等的三角形有5个;的面积是面积的;其中一定正确结论有???
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题
如图,AD是的中线,点E在AC上,BE交AD于点F,,则_______.
如图,在中,D是BC上的点,E是AC上的点,AD与BE相交于点F,若AE::4,BD::3,则BF:FE的值是
____________.
如图,直线,若,,,则线段的长是_____________?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
在平面直角坐标系中,已知,,,E是x轴上一点,双曲线经过CE的中点P,直线PB交AC于点若,则________.
将两块完全相同的等腰直角三角板摆放成如图所示的样子,假设图中的所有点、线都在同一平面内,图中有相似不包括全等三角形有______对.
如图,已知点O是中BC边上的中点,且,则______.
三、解答题
如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接作于点E,交半圆O于点已知,.
求证:∽.
求半圆O的半径r的长.
如图,在的方格中,点A,B,C为格点.
利用无刻度的直尺在图1中画的中线BE和重心G;
在图2中标注的外心O并画出外接圆及切线CP.
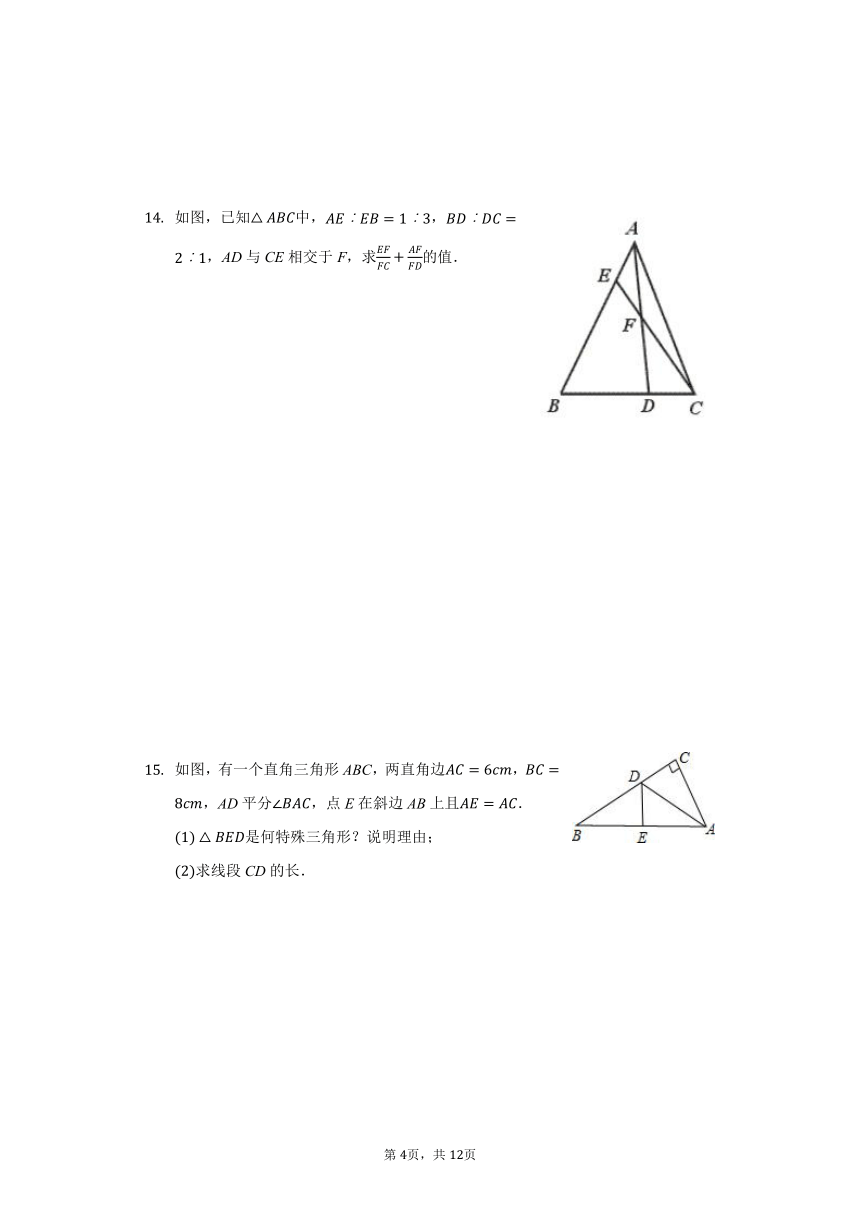
如图,已知中,,,AD与CE相交于F,求的值.
如图,有一个直角三角形ABC,两直角边,,AD平分,点E在斜边AB上且.
是何特殊三角形?说明理由;
求线段CD的长.
答案和解析
A
解:如图1,连接BD、CD,
,
为的直径,
,
,
弦AD平分,
,
,
在和中,
∽,
,即,
解得.
2.
C
3.
B
解:在梯形ABCD中,
,
∽
,
∽,∽,∽,∽
共有5对相似三角形?
4.
A
解:如图
当点N与点B重合时,点F就是BM的中点,
过点F作交AD于G,
当点N与点A重合时,点F就是AM与GF的交点,
由平行线分线段成比例定理可知随着点N从A到B的运动过程中,点F就在线段上移动,
线段EF在运动过程中所扫过图形为三角形,
为AM中点,F为BM中点,
,
过点E作于H,交DC于I,过点E作于P,
过点D作于K,
,,
为矩形,
,,
,
,
,,
为DM的中点,
为CM中点,
,
设,则,,,
,
.
5.
D
解:是的重心,
线段AD,BE,CF是的三条中线,故错误;
,,故正确;
是的重心,
,
又与的高相等,
与的面积相等,
同理可知:与,与面积相等,并且都为面积的一半,
图中与面积相等的三角形个数为5个,故正确;
是的重心,
,故正确;
,
的面积是面积的,故正确.
故其中正确的结论有,共4个.
6.
解:如图,过点D作,交AC于点G;
则,
设,则;
,,
,
.
7.
解:过E作交BC于G.
,
,
,
.
,
,
又,
,
8.
3
解:,
,
,,,
,
9.
或
解:过P作PM平行AC交x轴于M,过P作PN垂直x轴于N
当Q在线段BP上时,如下图:?
,
,
,
,
,,
,
是CE中点,
坐标
坐标
;
?当Q在线段BP的延长线上时,如下图:?
,
,
的面积等于的面积的7倍,
,
,,
,
是CE中点,
坐标
坐标
.
综上所述:或.
10.
3
解:有3对相似三角形.
,,
∽.
,,
∽.
,
.
,
∽.
11.
解:过B作,交DE于点F,
,
,,
又O为BC的中点,,
在和中,
,
≌,
,
,,
又,,
,
则.
12.
证明:切半圆O于点D,
,
,
,
,
又,
∽.
解:在中,,,
,
∽.
,即,
解得:.
13.
解:如图所示,BE和点G即为所求;
如图所示,和PC即为所求.
14.
解:过E作,交AD于G,如图,
则有,即,得:,
,
过点D作,交CE于H,则,
,
.
15.
解:是直角三角形,理由是:
平分,,,AD为公共边,≌,,,
是直角三角形;
≌,,,
,,∽,,
两直角边,,,
,解得.
第2页,共2页
第1页,共1页
班级:___________姓名:___________得分:___________
一、选择题
如图,AB为的直径,C为上一点,弦AD平分,交BC于点E,,,则DE的长为
A.
B.
C.
2
D.
在中,点D,E,F分别在边AB,AC,BC上,若,,则下面所列比例式中正确的是
A.
B.
C.
D.
如图,在四边形ABCD中,,且AC与BD相交于点O,过点O作,分别交AB,CD于E,F,则图中相似的三角形共有【】
A.
6对
B.
5对
C.
4对
D.
3对
如图,在四边形ABCD中,,,,,点M为BC上异于B、C的一定点,点N为AB上的一动点,E、F分别为DM、MN的中点,当N从A到B的运动过程中,线段EF扫过图形的面积为
A.
4
B.
C.
5
D.
6
如图,在中,点F,D,E分别是边AB,BC,AC上的点,且AD,BE,CF相交于点O,若点O是的重心则以下结论:线段AD,BE,CF是的三条角平分线;的面积是面积的一半;图中与面积相等的三角形有5个;的面积是面积的;其中一定正确结论有???
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题
如图,AD是的中线,点E在AC上,BE交AD于点F,,则_______.
如图,在中,D是BC上的点,E是AC上的点,AD与BE相交于点F,若AE::4,BD::3,则BF:FE的值是
____________.
如图,直线,若,,,则线段的长是_____________?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
在平面直角坐标系中,已知,,,E是x轴上一点,双曲线经过CE的中点P,直线PB交AC于点若,则________.
将两块完全相同的等腰直角三角板摆放成如图所示的样子,假设图中的所有点、线都在同一平面内,图中有相似不包括全等三角形有______对.
如图,已知点O是中BC边上的中点,且,则______.
三、解答题
如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接作于点E,交半圆O于点已知,.
求证:∽.
求半圆O的半径r的长.
如图,在的方格中,点A,B,C为格点.
利用无刻度的直尺在图1中画的中线BE和重心G;
在图2中标注的外心O并画出外接圆及切线CP.
如图,已知中,,,AD与CE相交于F,求的值.
如图,有一个直角三角形ABC,两直角边,,AD平分,点E在斜边AB上且.
是何特殊三角形?说明理由;
求线段CD的长.
答案和解析
A
解:如图1,连接BD、CD,
,
为的直径,
,
,
弦AD平分,
,
,
在和中,
∽,
,即,
解得.
2.
C
3.
B
解:在梯形ABCD中,
,
∽
,
∽,∽,∽,∽
共有5对相似三角形?
4.
A
解:如图
当点N与点B重合时,点F就是BM的中点,
过点F作交AD于G,
当点N与点A重合时,点F就是AM与GF的交点,
由平行线分线段成比例定理可知随着点N从A到B的运动过程中,点F就在线段上移动,
线段EF在运动过程中所扫过图形为三角形,
为AM中点,F为BM中点,
,
过点E作于H,交DC于I,过点E作于P,
过点D作于K,
,,
为矩形,
,,
,
,
,,
为DM的中点,
为CM中点,
,
设,则,,,
,
.
5.
D
解:是的重心,
线段AD,BE,CF是的三条中线,故错误;
,,故正确;
是的重心,
,
又与的高相等,
与的面积相等,
同理可知:与,与面积相等,并且都为面积的一半,
图中与面积相等的三角形个数为5个,故正确;
是的重心,
,故正确;
,
的面积是面积的,故正确.
故其中正确的结论有,共4个.
6.
解:如图,过点D作,交AC于点G;
则,
设,则;
,,
,
.
7.
解:过E作交BC于G.
,
,
,
.
,
,
又,
,
8.
3
解:,
,
,,,
,
9.
或
解:过P作PM平行AC交x轴于M,过P作PN垂直x轴于N
当Q在线段BP上时,如下图:?
,
,
,
,
,,
,
是CE中点,
坐标
坐标
;
?当Q在线段BP的延长线上时,如下图:?
,
,
的面积等于的面积的7倍,
,
,,
,
是CE中点,
坐标
坐标
.
综上所述:或.
10.
3
解:有3对相似三角形.
,,
∽.
,,
∽.
,
.
,
∽.
11.
解:过B作,交DE于点F,
,
,,
又O为BC的中点,,
在和中,
,
≌,
,
,,
又,,
,
则.
12.
证明:切半圆O于点D,
,
,
,
,
又,
∽.
解:在中,,,
,
∽.
,即,
解得:.
13.
解:如图所示,BE和点G即为所求;
如图所示,和PC即为所求.
14.
解:过E作,交AD于G,如图,
则有,即,得:,
,
过点D作,交CE于H,则,
,
.
15.
解:是直角三角形,理由是:
平分,,,AD为公共边,≌,,,
是直角三角形;
≌,,,
,,∽,,
两直角边,,,
,解得.
第2页,共2页
第1页,共1页
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
