27.2.1 相似三角形的判定第一课时 教学课件(共23张PPT)
文档属性
| 名称 | 27.2.1 相似三角形的判定第一课时 教学课件(共23张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 687.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览








文档简介
教学目标
1、会用符号“∽”表示相似三角形如△ABC ∽ △;知道当△ABC、△的相似比为k时,△与△ABC的相似比为1/k.理解掌握平行线分线段成比例定理
2、在平行线分线段成比例定理探究过程中,让学生运用“操作—比较—发现—归纳”分析问题.
3、在探究平行线分线段成比例定理过程中,培养学生与他人交流、合作的意识和品质.
重点难点
教学重点:
理解掌握平行线分线段成比例定理及应用.
教学难点:
掌握平行线分线段成比例定理应用.
温故知新
定义:
如果两个图形形状相同,但大小不一定相等,那么这两个图形相似。(相似的符号:∽)
知识清单1
温故知新
判定:
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似。
知识清单2
温故知新
相似比
相似多边形的对应边的比叫相似比。相似比为1时,相似的两个图形全等。
知识清单2
温故知新
性质
1.相似多边形的对应角相等,对应边的比相等。
2.相似多边形的周长比等于相似比。
3.相似多边形的面积比等于相似比的平方。
知识清单2
课程导入
阅读课本P29--P30,思考下列问题:
(1)相似三角形的定义
(2)平行线分线段成比例的基本事实
(3)相似三角形的判定方法——“平行定理”
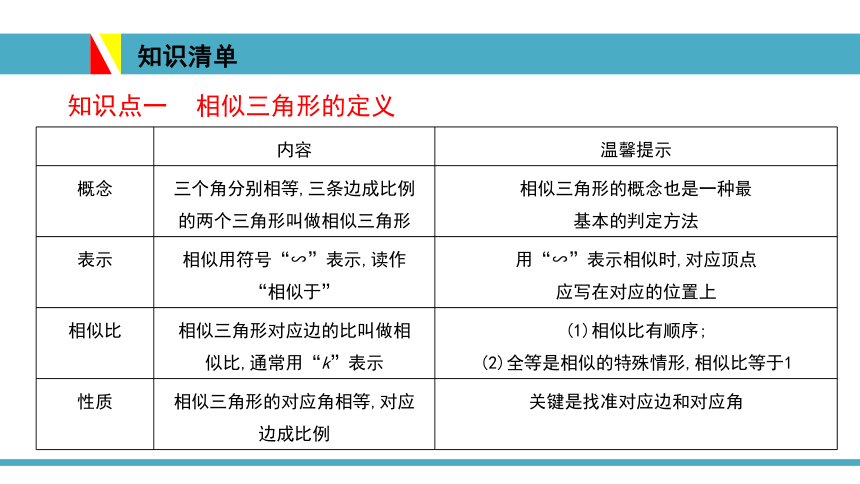
知识点一????相似三角形的定义
内容
温馨提示
概念
三个角分别相等,三条边成比例
的两个三角形叫做相似三角形
相似三角形的概念也是一种最
基本的判定方法
表示
相似用符号“∽”表示,读作
“相似于”
用“∽”表示相似时,对应顶点
应写在对应的位置上
相似比
相似三角形对应边的比叫做相
似比,通常用“k”表示
(1)相似比有顺序;
(2)全等是相似的特殊情形,相似比等于1
性质
相似三角形的对应角相等,对应
边成比例
关键是找准对应边和对应角
内容
图例
基本
事实
两条直线被一组平行线所截,所
得的对应线段成比例
?
由l3∥l4∥l5,
得 ?=? ,? = ,? =?
应用
平行于三角形一边的直线截其
他两边(或两边的延长线),所得
的对应线段成比例
?
由DE∥BC,得?=?
知识点二????平行线分线段成比例
知识点三????相似三角形的判定方法——“平行定理”
内容
类别
“A”型
“X”型
平行于三角形一边的
直线和其他两边相交,
所构成的三角形与原
三角形相似
DE与AB,AC相交
DE与AB,AC的延长线
相交
DE与AB,AC的反向延
长线相交
?
?
?
例1.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
解:根据相似三角形的判定定理逐一分析即可.
C
'
'
'
例2.已知△ABC∽△A'B'C',若AC=3,A'C'=1.8,则△A'B'C'与△ABC的相似比
为?( )
A.? ????B.? ????C.? ????D.?
解:????D 对应边的比等于相似比,且有顺序性,故△A'B'C'与△ABC的相似比为
?= ?= ?.故选D.
D
2.在△ABC和△A'B'C'中,AB=AC,A'B'=A'C',若添加一个条件可使两个三角形相似,甲添加的条件是∠A=∠A'=60°;乙添加的条件是∠A=∠A'=90°.对于甲、乙添加的条件判断正确的是?( )
A.甲对乙错 ????B.甲错乙对 C.两人都对 ????D.两人都错
解????C 甲添加条件后,两个三角形都是等边三角形,两个三角形的三个角都是60°,三边成比例,这两个三角形相似;乙添加条件后,两个三角形都是等腰直角三角形,三个角分别为90°,45°,45°,三个角分别相等,由勾股定理可知,斜边是直角边的?倍,故这两个三角形的三边成比例,两个三角形相似.
故甲、乙添加的条件都正确,故选C.
C
例3 如图,若l1∥l2∥l3,则下列各式错误的是?( )
?
A.? =? ?? ??B. =?
C.? =? ???? D.? =?
解∵l1∥l2∥l3,
∴?=?,?=?,
∴?=?,
故选D.
D
1.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
1.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
(2)若AB:BC=2:5,DF=10,求EF的长
例4 .如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E、F分别在AB、AC上,且EF∥BC,交AD于点G,则图中的相似三角形有?( )
A.5对 ????B.6对 ????C.7对 ????D.8对
C
解:∵EF∥BC,
∴△AEG∽△ABD,△AGF∽△ADC,△AEF∽△ABC.
∵AB=AC且AD⊥BC,
∴△AEG≌△AFG,△ABD≌△ACD,
∴△AEG∽△ACD,△AFG∽△ABD,
∴题图中共有7对相似三角形.
故选C.
1.如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
(1)求 的值;
(2)求BC的长.
1.如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
(2)求BC的长.
1、相似三角形的定义
2、平行线分线段成比例
3、相似三角形的判定方法——“平行定理”
1、会用符号“∽”表示相似三角形如△ABC ∽ △;知道当△ABC、△的相似比为k时,△与△ABC的相似比为1/k.理解掌握平行线分线段成比例定理
2、在平行线分线段成比例定理探究过程中,让学生运用“操作—比较—发现—归纳”分析问题.
3、在探究平行线分线段成比例定理过程中,培养学生与他人交流、合作的意识和品质.
重点难点
教学重点:
理解掌握平行线分线段成比例定理及应用.
教学难点:
掌握平行线分线段成比例定理应用.
温故知新
定义:
如果两个图形形状相同,但大小不一定相等,那么这两个图形相似。(相似的符号:∽)
知识清单1
温故知新
判定:
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似。
知识清单2
温故知新
相似比
相似多边形的对应边的比叫相似比。相似比为1时,相似的两个图形全等。
知识清单2
温故知新
性质
1.相似多边形的对应角相等,对应边的比相等。
2.相似多边形的周长比等于相似比。
3.相似多边形的面积比等于相似比的平方。
知识清单2
课程导入
阅读课本P29--P30,思考下列问题:
(1)相似三角形的定义
(2)平行线分线段成比例的基本事实
(3)相似三角形的判定方法——“平行定理”
知识点一????相似三角形的定义
内容
温馨提示
概念
三个角分别相等,三条边成比例
的两个三角形叫做相似三角形
相似三角形的概念也是一种最
基本的判定方法
表示
相似用符号“∽”表示,读作
“相似于”
用“∽”表示相似时,对应顶点
应写在对应的位置上
相似比
相似三角形对应边的比叫做相
似比,通常用“k”表示
(1)相似比有顺序;
(2)全等是相似的特殊情形,相似比等于1
性质
相似三角形的对应角相等,对应
边成比例
关键是找准对应边和对应角
内容
图例
基本
事实
两条直线被一组平行线所截,所
得的对应线段成比例
?
由l3∥l4∥l5,
得 ?=? ,? = ,? =?
应用
平行于三角形一边的直线截其
他两边(或两边的延长线),所得
的对应线段成比例
?
由DE∥BC,得?=?
知识点二????平行线分线段成比例
知识点三????相似三角形的判定方法——“平行定理”
内容
类别
“A”型
“X”型
平行于三角形一边的
直线和其他两边相交,
所构成的三角形与原
三角形相似
DE与AB,AC相交
DE与AB,AC的延长线
相交
DE与AB,AC的反向延
长线相交
?
?
?
例1.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
解:根据相似三角形的判定定理逐一分析即可.
C
'
'
'
例2.已知△ABC∽△A'B'C',若AC=3,A'C'=1.8,则△A'B'C'与△ABC的相似比
为?( )
A.? ????B.? ????C.? ????D.?
解:????D 对应边的比等于相似比,且有顺序性,故△A'B'C'与△ABC的相似比为
?= ?= ?.故选D.
D
2.在△ABC和△A'B'C'中,AB=AC,A'B'=A'C',若添加一个条件可使两个三角形相似,甲添加的条件是∠A=∠A'=60°;乙添加的条件是∠A=∠A'=90°.对于甲、乙添加的条件判断正确的是?( )
A.甲对乙错 ????B.甲错乙对 C.两人都对 ????D.两人都错
解????C 甲添加条件后,两个三角形都是等边三角形,两个三角形的三个角都是60°,三边成比例,这两个三角形相似;乙添加条件后,两个三角形都是等腰直角三角形,三个角分别为90°,45°,45°,三个角分别相等,由勾股定理可知,斜边是直角边的?倍,故这两个三角形的三边成比例,两个三角形相似.
故甲、乙添加的条件都正确,故选C.
C
例3 如图,若l1∥l2∥l3,则下列各式错误的是?( )
?
A.? =? ?? ??B. =?
C.? =? ???? D.? =?
解∵l1∥l2∥l3,
∴?=?,?=?,
∴?=?,
故选D.
D
1.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
1.如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
(1)若AB=3,BC=5,DE=4,求EF的长;
(2)若AB:BC=2:5,DF=10,求EF的长
例4 .如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E、F分别在AB、AC上,且EF∥BC,交AD于点G,则图中的相似三角形有?( )
A.5对 ????B.6对 ????C.7对 ????D.8对
C
解:∵EF∥BC,
∴△AEG∽△ABD,△AGF∽△ADC,△AEF∽△ABC.
∵AB=AC且AD⊥BC,
∴△AEG≌△AFG,△ABD≌△ACD,
∴△AEG∽△ACD,△AFG∽△ABD,
∴题图中共有7对相似三角形.
故选C.
1.如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
(1)求 的值;
(2)求BC的长.
1.如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
(2)求BC的长.
1、相似三角形的定义
2、平行线分线段成比例
3、相似三角形的判定方法——“平行定理”
