26.2 实际问题与反比例函数 教学课件(共20张PPT)
文档属性
| 名称 | 26.2 实际问题与反比例函数 教学课件(共20张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 574.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览







文档简介
教学目标
重点:运用反比例函数的解析式和图像表示问题情景中成反比例的量之间的关系,进而利用反比例函数的图像及性质解决问题。
难点:根据问题列方程
重点难点
1.使学生理解并掌握反比例函数的概念
2.能判断一个给定的函数是否为反比例函数,并会用待定系数法求解析式
3.能根据实际问题中的条件确定反比例函数解析式,体会函数的模型思想
温故知新
反比例的画法分三个步骤:⑴列表;⑵描点;⑶连线。
作反比例函数的图像时应注意以下几点:
①列表时选取的数值宜对称选取;
②列表时选取的数值越多,画的图像越精确;
③连线时,必须根据自变量大小从左至右(或从右至左)用光滑的曲线连接,切忌画成折线;
④画图像时,它的两个分支应全部画出,但切忌将图像与坐标轴相交。
知识清单1 反比例函数图像的画法
温故知新
1、反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、第三象限或第二、第四象限;
2、由于反比例函数中自变量函数中自变量,函数值,所以它的图像与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
3、双曲线既是中心对称图形(对称中心是原点),又是轴对称图形(对称轴是直线 y =x 和直线 y =-x ).
知识清单2 反比例函数图像的初步特征
温故知新
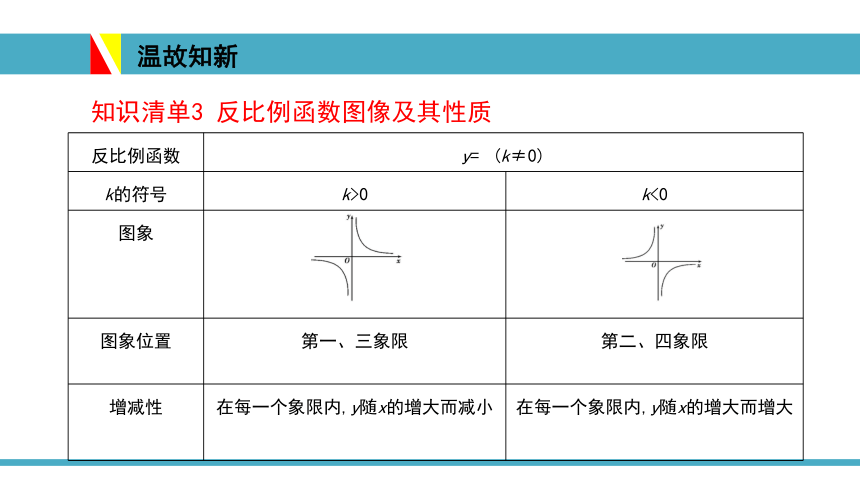
知识清单3 反比例函数图像及其性质
反比例函数
y=?(k≠0)
k的符号
k>0
k<0
图象
?
?
图象位置
第一、三象限
第二、四象限
增减性
在每一个象限内,y随x的增大而减小
在每一个象限内,y随x的增大而增大
温故知新
知识清单4 k的的几何意义
如图所示,过双曲线上任一点P(x,y)分别作x轴、y轴的垂线,E、F分别为垂足,
则
情境导入
阅读课本P12-P15,思考:
1、如何根据实际问题中变量之间的数量关系建立函数解析式?
2、解答反比例函数实际问题时x的取值范围
随堂练习
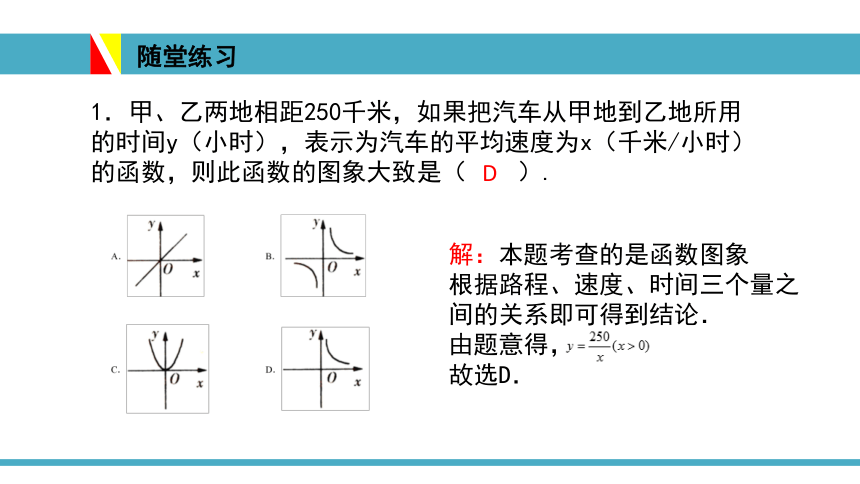
1.甲、乙两地相距250千米,如果把汽车从甲地到乙地所用的时间y(小时),表示为汽车的平均速度为x(千米/小时)的函数,则此函数的图象大致是( ).
解:本题考查的是函数图象
根据路程、速度、时间三个量之间的关系即可得到结论.
由题意得,
故选D.
D
随堂练习
2.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
解:由“这批煤燃烧的天数=这批煤的总量÷每天烧煤的吨数”
10
可得:
故选A.
A
随堂练习
3.在公式ρ= 中,当质量m一定时,密度与体积V之间的函数关系可用图象表示为( )
B
随堂练习
4.实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为___________,当S=2 cm2时, R=______________(Ω)
R=
14.5
随堂练习
5.三角形的面积是20cm2,它的底边a(单位:cm)与这个底边上的高h(单位:cm)的函数关系式为a=________.
随堂练习
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流不能超过6A,那么用电器的可变电阻R应控制在( )
解:设反比例函数关系式为:I= ,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I= ,
当I≤6时,则 ≤6,R≥1,
故选:C.
C
随堂练习
7.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点;
(2)猜测并确定y与x之间的函数关系式,并画出图像;
(3)设经营此贺卡的销售利润为w元,求出w与x之间的函数关系式. 若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
随堂练习
7.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点;
解:(1)根据已知描点即可;
随堂练习
7.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(2)猜测并确定y与x之间的函数关系式,并画出图像;
(2)由表可知,xy=60,
∴y (x>0),函数图象如图:
随堂练习
(3)设经营此贺卡的销售利润为w元,求出w与x之间的函数关系式. 若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
(3)根据题意,得:
W=(x﹣2)?y=(x﹣2)? =60 ;
∵x≤10,∴ ≤12,则60 ≤48,
即当x=10时,W取得最大值,最大值为48元.
答:当日销售单价x定为10元/个时,才能获得最大日销售利润,最大利润是48元.
课堂小结
1.根据实际列反比例函数
2.注意k的取值范围
3.注意根据生活实际确定x的取值范围
重点:运用反比例函数的解析式和图像表示问题情景中成反比例的量之间的关系,进而利用反比例函数的图像及性质解决问题。
难点:根据问题列方程
重点难点
1.使学生理解并掌握反比例函数的概念
2.能判断一个给定的函数是否为反比例函数,并会用待定系数法求解析式
3.能根据实际问题中的条件确定反比例函数解析式,体会函数的模型思想
温故知新
反比例的画法分三个步骤:⑴列表;⑵描点;⑶连线。
作反比例函数的图像时应注意以下几点:
①列表时选取的数值宜对称选取;
②列表时选取的数值越多,画的图像越精确;
③连线时,必须根据自变量大小从左至右(或从右至左)用光滑的曲线连接,切忌画成折线;
④画图像时,它的两个分支应全部画出,但切忌将图像与坐标轴相交。
知识清单1 反比例函数图像的画法
温故知新
1、反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、第三象限或第二、第四象限;
2、由于反比例函数中自变量函数中自变量,函数值,所以它的图像与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
3、双曲线既是中心对称图形(对称中心是原点),又是轴对称图形(对称轴是直线 y =x 和直线 y =-x ).
知识清单2 反比例函数图像的初步特征
温故知新
知识清单3 反比例函数图像及其性质
反比例函数
y=?(k≠0)
k的符号
k>0
k<0
图象
?
?
图象位置
第一、三象限
第二、四象限
增减性
在每一个象限内,y随x的增大而减小
在每一个象限内,y随x的增大而增大
温故知新
知识清单4 k的的几何意义
如图所示,过双曲线上任一点P(x,y)分别作x轴、y轴的垂线,E、F分别为垂足,
则
情境导入
阅读课本P12-P15,思考:
1、如何根据实际问题中变量之间的数量关系建立函数解析式?
2、解答反比例函数实际问题时x的取值范围
随堂练习
1.甲、乙两地相距250千米,如果把汽车从甲地到乙地所用的时间y(小时),表示为汽车的平均速度为x(千米/小时)的函数,则此函数的图象大致是( ).
解:本题考查的是函数图象
根据路程、速度、时间三个量之间的关系即可得到结论.
由题意得,
故选D.
D
随堂练习
2.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
解:由“这批煤燃烧的天数=这批煤的总量÷每天烧煤的吨数”
10
可得:
故选A.
A
随堂练习
3.在公式ρ= 中,当质量m一定时,密度与体积V之间的函数关系可用图象表示为( )
B
随堂练习
4.实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为___________,当S=2 cm2时, R=______________(Ω)
R=
14.5
随堂练习
5.三角形的面积是20cm2,它的底边a(单位:cm)与这个底边上的高h(单位:cm)的函数关系式为a=________.
随堂练习
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流不能超过6A,那么用电器的可变电阻R应控制在( )
解:设反比例函数关系式为:I= ,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I= ,
当I≤6时,则 ≤6,R≥1,
故选:C.
C
随堂练习
7.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点;
(2)猜测并确定y与x之间的函数关系式,并画出图像;
(3)设经营此贺卡的销售利润为w元,求出w与x之间的函数关系式. 若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
随堂练习
7.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点;
解:(1)根据已知描点即可;
随堂练习
7.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(2)猜测并确定y与x之间的函数关系式,并画出图像;
(2)由表可知,xy=60,
∴y (x>0),函数图象如图:
随堂练习
(3)设经营此贺卡的销售利润为w元,求出w与x之间的函数关系式. 若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
(3)根据题意,得:
W=(x﹣2)?y=(x﹣2)? =60 ;
∵x≤10,∴ ≤12,则60 ≤48,
即当x=10时,W取得最大值,最大值为48元.
答:当日销售单价x定为10元/个时,才能获得最大日销售利润,最大利润是48元.
课堂小结
1.根据实际列反比例函数
2.注意k的取值范围
3.注意根据生活实际确定x的取值范围
