北师大版七年级上册数学 第五章 复习题 课件(共26张ppt)
文档属性
| 名称 | 北师大版七年级上册数学 第五章 复习题 课件(共26张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 06:06:53 | ||
图片预览








文档简介
教学目标
1.通过复习加深对一元一次方程的理解,进一步巩固一元一次方程的解法
2.掌握用一元一次方程解决实际问题,提高分析问题和解决问题的能力
3.培养良好的整理和复习的良好习惯
解析几何的创立者笛卡尔
任何问题都可以转化为数学问题
任何数学问题都可以转化为代数问题
任何代数问题都可以转化为方程问题
本章主要内容
1.一元一次方程及方程的解的概念
2.等式的基本性质
3.解方程
4.利用一元一次方程解决实际问题等
主要热门考点可概括为:两个概念、一个性质、一个解法、一个应用
一、一元一次方程概念
在一个方程中,只含有_____个未知数,而且方程中的代数式都是整式,未知数的指数是______次,这样的方程叫做一元一次方程。
一
一
一
1
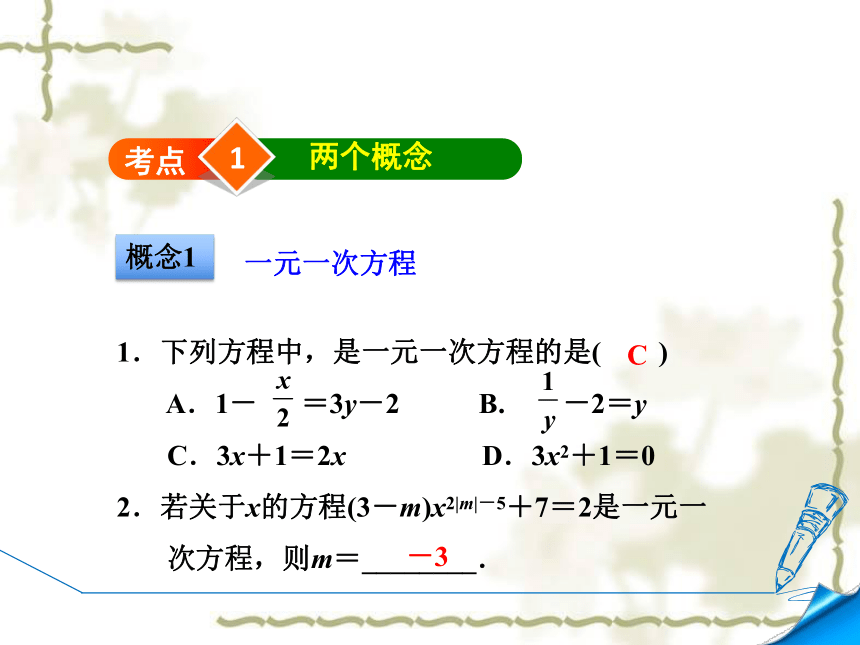
考点
两个概念
1.下列方程中,是一元一次方程的是( )
A.1- =3y-2 B. -2=y
C.3x+1=2x D.3x2+1=0
2.若关于x的方程(3-m)x2|m|-5+7=2是一元一
次方程,则m=________.
概念1
一元一次方程
C
-3
二、方程的解
方程的解:使方程左右两边的_______的未知数的值,叫做方程的解
相等
3.若关于x的方程ax+3=4x+1的解为正整数,
则整数a 的值为( )
A.2或3 B.4
C.5 D.6
概念2
方程的解
A
三、等式的基本性质
性质1:等式两边同时加(或减)______所得结果仍是等式。
性质2:等式两边同时乘_________(或除以__________),所得结果仍是等式。
同一个代数式
同一个数
同一个不为0的数
2、如果a=b,那么下列结论正确的是( )
A.
B.
C.
D.
C
四、一元一次方程的解法
解一元一次方程,一般要__________、
_______、________、____________、
________________ 等步骤,把一个一
元一次方程“ ”成x=a的形式。
去分母
去括号
移项
合并同类项
未知数的系数为1
转化
3
考点
一个解法——一元一次方程的解法
6.解下列方程:
(1)12-(3x-5)=7-5x;
解:
去括号,得12-3x+5=7-5x.
移项、合并同类项,得2x=-10.
系数化为1,得x=-5.
小明做了一道题,你来判断对不对?
解方程
2(3x-1)=1-4x-1
6x-2=1-4x-1
6x+4x=1-1+2
10x=2
X=
2(3x-1)=6-(4x-1)
6x-2=6-4x+1
6x+4x=6+1+2
10x=9
X=
变形名称
注意事项
去分母
去括号
移项
合并同类项
系数化为1
防止漏乘(尤其是整数项),注意添括号
注意变号,防止漏乘
移项要变号
计算要仔细,不要出差错
计算要仔细,分子分母不要颠倒
(1)
解:
(2)去分母,得2(2x-5)+3(3-x)=12.
去括号,得4x-10+9-3x=12.
移项、合并同类项,得x=13.
4
考点
一个应用——一元一次方程的实际应用
7.某校为了做好大课间活动,计划用400元购买10
件体育用品,备选体育用品及价格如下表:
备选体育用品
篮球
排球
羽毛球拍
价格
50元/个
40元/个
25元/副
4
考点
一个应用——一元一次方程的实际应用
7.某校为了做好大课间活动,计划用400元购买10
件体育用品,备选体育用品及价格如下表:
备选体育用品
篮球
排球
羽毛球拍
价格
50元/个
40元/个
25元/副
(1)若400元全部用来购买篮球和羽毛球拍共10件,则
各自购买多少件?
(2)400元全部用来购买篮球、排球和羽毛球拍三种共
10件,能实现吗?若能,写出购买方案即可;若
不能,请说明理由.
(1)若400元全部用来购买篮球和羽毛球拍共10件,则
各自购买多少件?
(2)400元全部用来购买篮球、排球和羽毛球拍三种共
10件,能实现吗?若能,写出购买方案即可;若
不能,请说明理由.
解:
(1)设购买篮球x个,则购买羽毛球拍(10-x)副.
由题意,得50x+25(10-x)=400.
解得x=6. 所以10-x=4.
答:购买篮球6个,羽毛球拍4副.
(2)能实现.购买篮球3个,排球5个,羽毛球拍2副.
9.甲厂有91名工人,乙厂有49名工人,为了赶
制一批产品又调来了100名工人,使甲厂的
人数比乙厂人数的3倍少12人,应往甲、乙
两厂各调多少名工人?
技巧1
列表分析数量关系法
点拨:
此题可以列表分析为:
再由题意列出方程求解.
?
原有人数
调入人数
甲厂
91
x
乙厂
49
100-x
解:
设应往甲厂调x名工人,
则往乙厂调(100-x)名工人,
依题意,得91+x=3(49+100-x)-12.
解这个方程,得x=86.
所以100-x=14.
故应往甲厂调86名工人,往乙厂调14名工人.
10. 某班有学生45人,选举甲、乙两人作为学生会
干部候选人,结果有40人赞成甲,有37人赞成
乙,对甲、乙都不赞成的人数是都赞成人数的
那么对甲、乙都赞成的有多少人?
技巧2
画图分析数量关系法
点拨:
题中涉及的各种量之间的关系如图所示,
通过图示列方程求解即可.
解:
设对甲、乙都赞成的有x人,
则都不赞成的有 x人.
由题意,得40+37-x+ x=45.
解得x=36.
故对甲、乙都赞成的有36人.
B
x+2x+56=589
1.通过复习加深对一元一次方程的理解,进一步巩固一元一次方程的解法
2.掌握用一元一次方程解决实际问题,提高分析问题和解决问题的能力
3.培养良好的整理和复习的良好习惯
解析几何的创立者笛卡尔
任何问题都可以转化为数学问题
任何数学问题都可以转化为代数问题
任何代数问题都可以转化为方程问题
本章主要内容
1.一元一次方程及方程的解的概念
2.等式的基本性质
3.解方程
4.利用一元一次方程解决实际问题等
主要热门考点可概括为:两个概念、一个性质、一个解法、一个应用
一、一元一次方程概念
在一个方程中,只含有_____个未知数,而且方程中的代数式都是整式,未知数的指数是______次,这样的方程叫做一元一次方程。
一
一
一
1
考点
两个概念
1.下列方程中,是一元一次方程的是( )
A.1- =3y-2 B. -2=y
C.3x+1=2x D.3x2+1=0
2.若关于x的方程(3-m)x2|m|-5+7=2是一元一
次方程,则m=________.
概念1
一元一次方程
C
-3
二、方程的解
方程的解:使方程左右两边的_______的未知数的值,叫做方程的解
相等
3.若关于x的方程ax+3=4x+1的解为正整数,
则整数a 的值为( )
A.2或3 B.4
C.5 D.6
概念2
方程的解
A
三、等式的基本性质
性质1:等式两边同时加(或减)______所得结果仍是等式。
性质2:等式两边同时乘_________(或除以__________),所得结果仍是等式。
同一个代数式
同一个数
同一个不为0的数
2、如果a=b,那么下列结论正确的是( )
A.
B.
C.
D.
C
四、一元一次方程的解法
解一元一次方程,一般要__________、
_______、________、____________、
________________ 等步骤,把一个一
元一次方程“ ”成x=a的形式。
去分母
去括号
移项
合并同类项
未知数的系数为1
转化
3
考点
一个解法——一元一次方程的解法
6.解下列方程:
(1)12-(3x-5)=7-5x;
解:
去括号,得12-3x+5=7-5x.
移项、合并同类项,得2x=-10.
系数化为1,得x=-5.
小明做了一道题,你来判断对不对?
解方程
2(3x-1)=1-4x-1
6x-2=1-4x-1
6x+4x=1-1+2
10x=2
X=
2(3x-1)=6-(4x-1)
6x-2=6-4x+1
6x+4x=6+1+2
10x=9
X=
变形名称
注意事项
去分母
去括号
移项
合并同类项
系数化为1
防止漏乘(尤其是整数项),注意添括号
注意变号,防止漏乘
移项要变号
计算要仔细,不要出差错
计算要仔细,分子分母不要颠倒
(1)
解:
(2)去分母,得2(2x-5)+3(3-x)=12.
去括号,得4x-10+9-3x=12.
移项、合并同类项,得x=13.
4
考点
一个应用——一元一次方程的实际应用
7.某校为了做好大课间活动,计划用400元购买10
件体育用品,备选体育用品及价格如下表:
备选体育用品
篮球
排球
羽毛球拍
价格
50元/个
40元/个
25元/副
4
考点
一个应用——一元一次方程的实际应用
7.某校为了做好大课间活动,计划用400元购买10
件体育用品,备选体育用品及价格如下表:
备选体育用品
篮球
排球
羽毛球拍
价格
50元/个
40元/个
25元/副
(1)若400元全部用来购买篮球和羽毛球拍共10件,则
各自购买多少件?
(2)400元全部用来购买篮球、排球和羽毛球拍三种共
10件,能实现吗?若能,写出购买方案即可;若
不能,请说明理由.
(1)若400元全部用来购买篮球和羽毛球拍共10件,则
各自购买多少件?
(2)400元全部用来购买篮球、排球和羽毛球拍三种共
10件,能实现吗?若能,写出购买方案即可;若
不能,请说明理由.
解:
(1)设购买篮球x个,则购买羽毛球拍(10-x)副.
由题意,得50x+25(10-x)=400.
解得x=6. 所以10-x=4.
答:购买篮球6个,羽毛球拍4副.
(2)能实现.购买篮球3个,排球5个,羽毛球拍2副.
9.甲厂有91名工人,乙厂有49名工人,为了赶
制一批产品又调来了100名工人,使甲厂的
人数比乙厂人数的3倍少12人,应往甲、乙
两厂各调多少名工人?
技巧1
列表分析数量关系法
点拨:
此题可以列表分析为:
再由题意列出方程求解.
?
原有人数
调入人数
甲厂
91
x
乙厂
49
100-x
解:
设应往甲厂调x名工人,
则往乙厂调(100-x)名工人,
依题意,得91+x=3(49+100-x)-12.
解这个方程,得x=86.
所以100-x=14.
故应往甲厂调86名工人,往乙厂调14名工人.
10. 某班有学生45人,选举甲、乙两人作为学生会
干部候选人,结果有40人赞成甲,有37人赞成
乙,对甲、乙都不赞成的人数是都赞成人数的
那么对甲、乙都赞成的有多少人?
技巧2
画图分析数量关系法
点拨:
题中涉及的各种量之间的关系如图所示,
通过图示列方程求解即可.
解:
设对甲、乙都赞成的有x人,
则都不赞成的有 x人.
由题意,得40+37-x+ x=45.
解得x=36.
故对甲、乙都赞成的有36人.
B
x+2x+56=589
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
