北师大版七年级上册数学 综合与实践 制作一个尽可能大的无盖长方体形盒子 课件(共20张ppt)
文档属性
| 名称 | 北师大版七年级上册数学 综合与实践 制作一个尽可能大的无盖长方体形盒子 课件(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览




文档简介
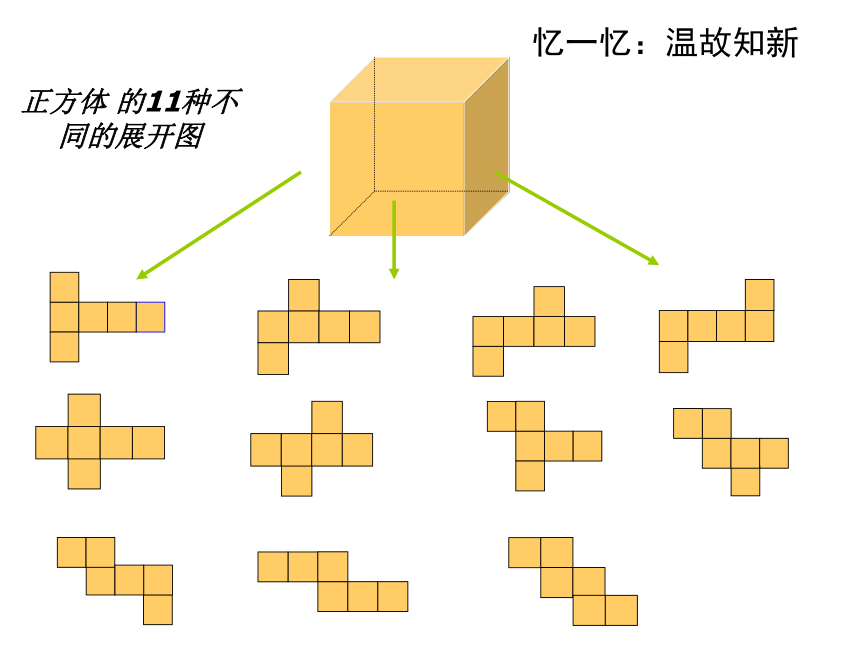
正方体的平面展开图有哪几种?你还记得吗?
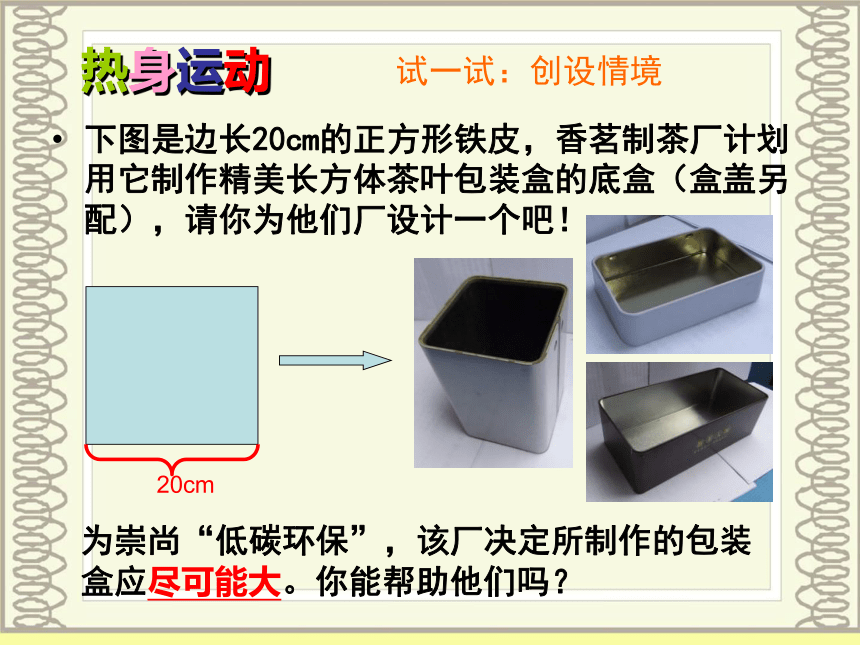
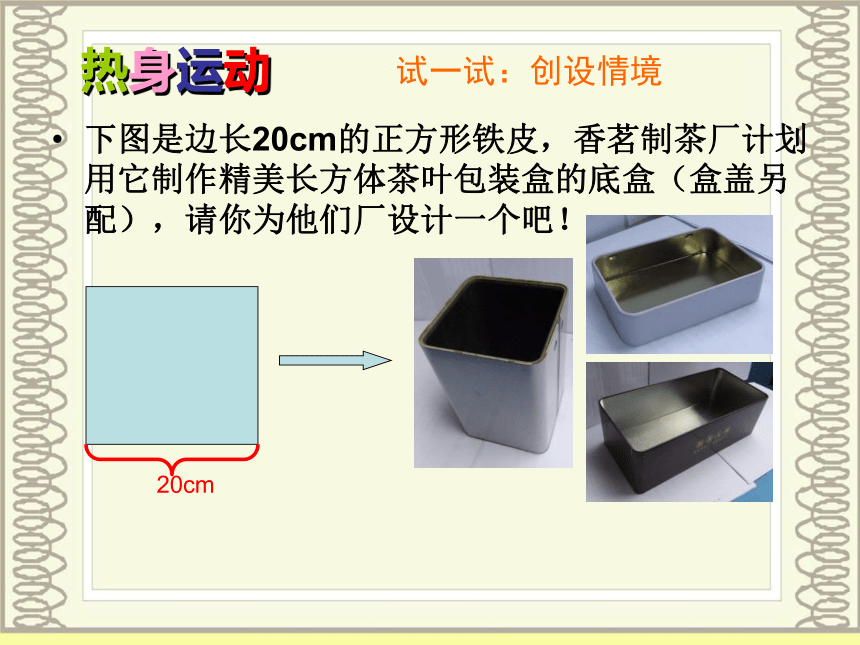
下图是边长20cm的正方形铁皮,香茗制茶厂计划用它制作精美长方体茶叶包装盒的底盒(盒盖另配),请你为他们厂设计一个吧!
下图是边长20cm的正方形铁皮,香茗制茶厂计划用它制作精美长方体茶叶包装盒的底盒(盒盖另配),请你为他们厂设计一个吧!
找一找:发现规律
找一找:发现规律
想一想:拓展提升
把14分拆为两个自然数之和,使它们的乘积尽可能大。
若是15呢?
若不限定把15分拆为两个自然数,乘积能大于56吗?
通过以上讨论,我们得到了按 制作尽可能大的长方体纸盒.
请同学们课后再探索一下:1、按别的展开图制作所得的尽可能大的长方体纸盒是否也是同样的容积呢?
2、既然要求“尽可能大”,若把剪下的重新利用,是否又能得到更大的容积?
课外尝试:撰写一份课题研究学习报告
忆一忆:温故知新
正方体 的11种不同的展开图
忆一忆:温故知新
试一试:创设情境
为崇尚“低碳环保”,该厂决定所制作的包装盒应尽可能大。你能帮助他们吗?
热身运动
20cm
制作一个尽可能大
的无盖长方体形盒子
揭题与审题
制作 尽可能大 无盖 长方体盒子
课题目标介绍
用一张规定边长的正方形铁皮 怎样才能制成一个无盖的长方体形盒子?
揭题与审题
怎样才能使制成的长方体形盒子
的容积尽可能大?
试一试:创设情境
热身运动
20cm
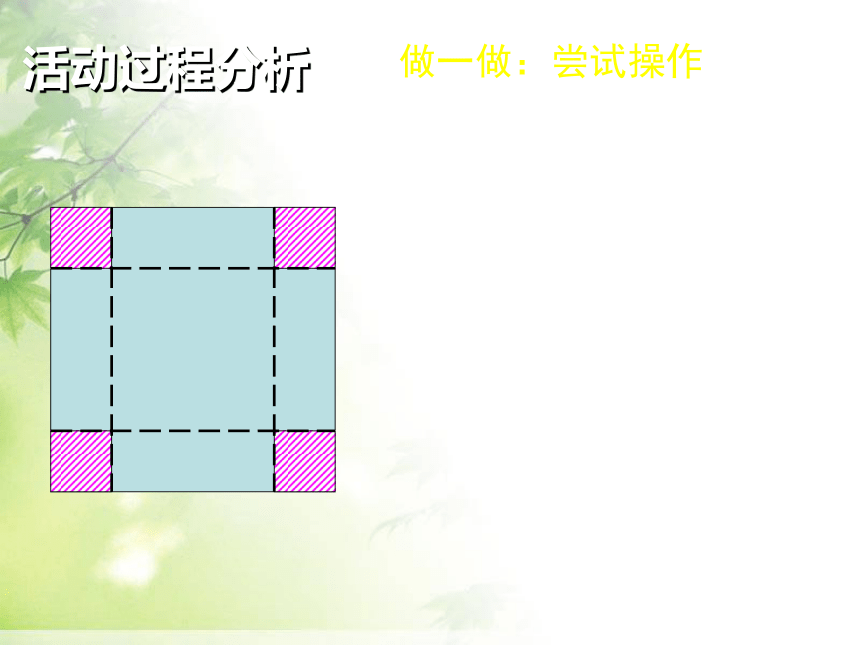
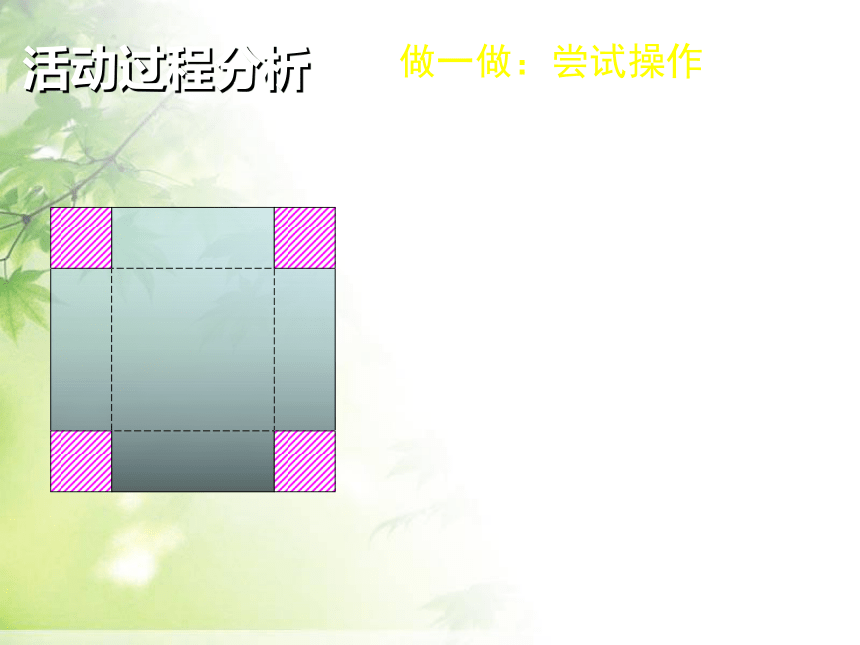
做一做:尝试操作
活动过程分析
做一做:尝试操作
活动过程分析
做一做:尝试操作
活动过程分析
猜一猜:大胆猜想
我们各组所制作的长方体盒子的大小都相等吗?
随着剪去的小正方形边长的增大,所折长方体的容积如何变化?
怎么验证上述这些猜想是否正确?
活动过程分析
议一议:建立模型
如何能更直观地表达纸盒容积的变化趋势?
活动过程分析
纸盒容积V=(20-2x) ·x
2
V
X
活动过程分析
20
x
V=(20-2x) ·x
2
1 2 3 4 5 6 7 8 9
V
9
8
7
6
5
4
3
2
1
X
活动过程分析
20
x
V=(20-2x) ·x
2
324 512 588 576 500 384 252 128 36
容积随边长变化的条型统计图:
活动过程分析
2
V
4
3.5
3
2.5
X
活动过程分析
20
x
V=(20-2x) ·x
2
512 562.5 588 591.5 576
V
X
活动过程分析
20
x
V=(20-2x) ·x
2
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9
590.4 591.9 592.5 592.4 591.5 589.8 587.4 594.3 580.5
想一想:拓展提升
热身运动
1×13 2×12
3×11 4×10
5×9 6×8
7×7
试一试:创设情境
活动过程分析
想一想:拓展提升
探究、解决实际问题的过程:
小结与感悟
数学
问题
数学化
建立
模型
观察、猜想
计算、推理
归纳
答案
华罗庚曾说:“宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,日用之繁,无处不用数学。”这是对数学与生活的精彩描述。
实际
问题
验证
下图是边长20cm的正方形铁皮,香茗制茶厂计划用它制作精美长方体茶叶包装盒的底盒(盒盖另配),请你为他们厂设计一个吧!
下图是边长20cm的正方形铁皮,香茗制茶厂计划用它制作精美长方体茶叶包装盒的底盒(盒盖另配),请你为他们厂设计一个吧!
找一找:发现规律
找一找:发现规律
想一想:拓展提升
把14分拆为两个自然数之和,使它们的乘积尽可能大。
若是15呢?
若不限定把15分拆为两个自然数,乘积能大于56吗?
通过以上讨论,我们得到了按 制作尽可能大的长方体纸盒.
请同学们课后再探索一下:1、按别的展开图制作所得的尽可能大的长方体纸盒是否也是同样的容积呢?
2、既然要求“尽可能大”,若把剪下的重新利用,是否又能得到更大的容积?
课外尝试:撰写一份课题研究学习报告
忆一忆:温故知新
正方体 的11种不同的展开图
忆一忆:温故知新
试一试:创设情境
为崇尚“低碳环保”,该厂决定所制作的包装盒应尽可能大。你能帮助他们吗?
热身运动
20cm
制作一个尽可能大
的无盖长方体形盒子
揭题与审题
制作 尽可能大 无盖 长方体盒子
课题目标介绍
用一张规定边长的正方形铁皮 怎样才能制成一个无盖的长方体形盒子?
揭题与审题
怎样才能使制成的长方体形盒子
的容积尽可能大?
试一试:创设情境
热身运动
20cm
做一做:尝试操作
活动过程分析
做一做:尝试操作
活动过程分析
做一做:尝试操作
活动过程分析
猜一猜:大胆猜想
我们各组所制作的长方体盒子的大小都相等吗?
随着剪去的小正方形边长的增大,所折长方体的容积如何变化?
怎么验证上述这些猜想是否正确?
活动过程分析
议一议:建立模型
如何能更直观地表达纸盒容积的变化趋势?
活动过程分析
纸盒容积V=(20-2x) ·x
2
V
X
活动过程分析
20
x
V=(20-2x) ·x
2
1 2 3 4 5 6 7 8 9
V
9
8
7
6
5
4
3
2
1
X
活动过程分析
20
x
V=(20-2x) ·x
2
324 512 588 576 500 384 252 128 36
容积随边长变化的条型统计图:
活动过程分析
2
V
4
3.5
3
2.5
X
活动过程分析
20
x
V=(20-2x) ·x
2
512 562.5 588 591.5 576
V
X
活动过程分析
20
x
V=(20-2x) ·x
2
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9
590.4 591.9 592.5 592.4 591.5 589.8 587.4 594.3 580.5
想一想:拓展提升
热身运动
1×13 2×12
3×11 4×10
5×9 6×8
7×7
试一试:创设情境
活动过程分析
想一想:拓展提升
探究、解决实际问题的过程:
小结与感悟
数学
问题
数学化
建立
模型
观察、猜想
计算、推理
归纳
答案
华罗庚曾说:“宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,日用之繁,无处不用数学。”这是对数学与生活的精彩描述。
实际
问题
验证
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
