人教版八年级数学上册:14.3.2 公式法 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册:14.3.2 公式法 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 195.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
公式法
—平方差公式法
1、什么叫分解因式?
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
一、激趣导入—复习旧知
2、已学过哪一种分解因式的方法?
提公因式法
3、【问题】你能将a2-b2分解因式吗?
你是如何思考的?
(a+b)(a-b)=a2-b2
a2-b2=(a+b)(a-b)
等号两边互换位置
运用公式法
把乘法公式的等号两边互换位置,可以把符合公式特点的多项式因式分解,这种方法叫公式法.
要将a2-b2进行因式分解,可以发现它没有公因式,不能用提公因式法分解因式.
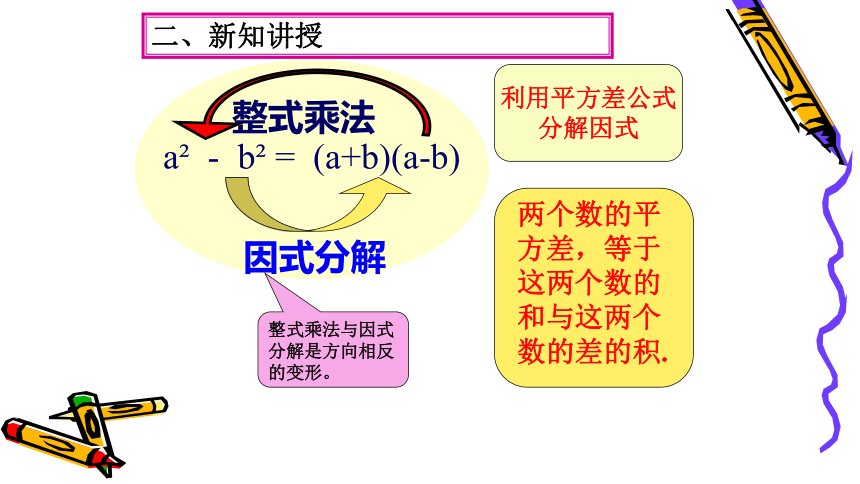
两个数的平
方差,等于这两个数的和与这两个数的差的积.
a?
-
b?
=
(a+b)(a-b)
因式分解
整式乘法
整式乘法与因式分解是方向相反的变形。
利用平方差公式
分解因式
二、新知讲授
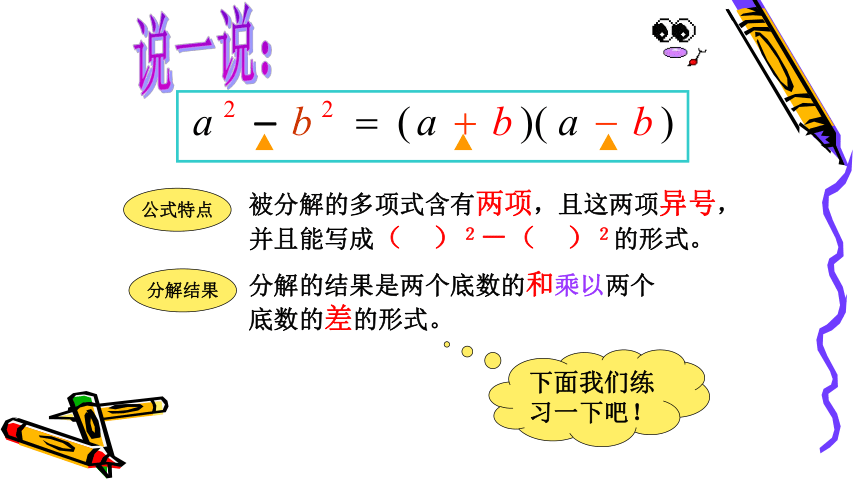
说一说:
被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
分解的结果是两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
下面我们练习一下吧!
公式特点
分解结果
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1)
m2
-1
(2)4m2
-9
(3)4m2+9
(4)
-x2
-25y2
(5)
-x2+25y2
=
m2
-12
=
(2m)2
-32
不能转化为平方差形式
不能转化为平方差形式
=
25y2-x2
=(5y)2
-x2
试一试,你能行!
练习
(1)x2-4=x2-22=
(x+2)(x-2);
(2)x2-16
=( )2-( )2
=( )( );
(3)9-y2=( )2-( )2
=( )·( );?
(4)1-a2
=( )2-( )2
=( )·( ).?
x
4
x+4
x-4
3
y
3+y
3-y
1
a
1+a
1-a
例1.分解因式
(1)
4x?
-
9
(2
)
(x+p)?
-
(x+q)?
4x?
-
9=
(2x)?
-
3?
a?
-
b?
=
(
a
+
b)(
a
-
b
)
(x+p)?-(x+q)?
=
(
2x
+
3
)(2x
-
3)
=[(x+p)+(x+q)][(x+p)
-(x+q)]
=(2x+p+q)(p-q)
三、精讲实练:应用平方差公式
例2、分解因式:
①x4-y4
②a3b-ab
解:
①x4-y4
=(x2)2-(y2)2=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y)
②a3b-ab=ab(a2-1)
=ab(a+1)(a-1)
若有公因式则先提公因式。然后再看能否用公式法。
分解因式,必须进行到每一个多项式都不能再分解为止。
(1)9a2-4b2;
(2)x2y-4y;
(3)(a+1)2-1;
(4)x4-1;
(5)(x+y+z)2-(x-y+z)2.
四、实练:应用平方进行分解因式
B
解析:
a2-9=(a+3)(a-3).故选B.
检测反馈
1.将a2-9分解因式的结果是
( )
A.(a+9)(a-9)
B.(a+3)(a-3)
C.(a+3)2
D.(a-3)2
五、达标检测
B
2.将(a-1)2-1分解因式,结果正确的是
( )
A.a(a-1)
B.a(a-2)
C.(a-2)(a-1)
D.(a-2)(a+1)
3.计算552-152的结果是
( )
A.40
B.1600
C.2400
D.2800
D
解析:
552-152
=(55+15)×(55-15)
=70×40
=2800.故选D.
4.用平方差公式分解因式.
(1)36-x
2
;
(2)-a
2+b
2
;
(3)x
2-16y
2;
(4)x
2y
2-z
2;
(1)
4x?-
m?n?
解:4x?-
m?n?
=(2x)?
-
(mn)?
=(2x+mn)(2x-mn)
解:
练一练!
注意:若有公因式则先提公因式。然后再看能否用公式法。
(1)1002-992
(2)682-672
(4)
5.52-4.52
8
15
(
)
2
7
15
(
)
2
-
(3)
看谁算的又快又准确!
比一比!
小结:我学会了什么?
1.如果多项式各项含有公因式,则第一步是提出这个公因式.
2.如果多项式各项没有公因式,则第一步考虑用公式分解因式.
3.第一步分解因式以后,所含的多项式还可以继续分解,则需要进一步分解因式.直到每个多项式因式都不能分解为止.
作业布置
小本公式法(1)
公式法
—平方差公式法
1、什么叫分解因式?
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
一、激趣导入—复习旧知
2、已学过哪一种分解因式的方法?
提公因式法
3、【问题】你能将a2-b2分解因式吗?
你是如何思考的?
(a+b)(a-b)=a2-b2
a2-b2=(a+b)(a-b)
等号两边互换位置
运用公式法
把乘法公式的等号两边互换位置,可以把符合公式特点的多项式因式分解,这种方法叫公式法.
要将a2-b2进行因式分解,可以发现它没有公因式,不能用提公因式法分解因式.
两个数的平
方差,等于这两个数的和与这两个数的差的积.
a?
-
b?
=
(a+b)(a-b)
因式分解
整式乘法
整式乘法与因式分解是方向相反的变形。
利用平方差公式
分解因式
二、新知讲授
说一说:
被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
分解的结果是两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
下面我们练习一下吧!
公式特点
分解结果
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1)
m2
-1
(2)4m2
-9
(3)4m2+9
(4)
-x2
-25y2
(5)
-x2+25y2
=
m2
-12
=
(2m)2
-32
不能转化为平方差形式
不能转化为平方差形式
=
25y2-x2
=(5y)2
-x2
试一试,你能行!
练习
(1)x2-4=x2-22=
(x+2)(x-2);
(2)x2-16
=( )2-( )2
=( )( );
(3)9-y2=( )2-( )2
=( )·( );?
(4)1-a2
=( )2-( )2
=( )·( ).?
x
4
x+4
x-4
3
y
3+y
3-y
1
a
1+a
1-a
例1.分解因式
(1)
4x?
-
9
(2
)
(x+p)?
-
(x+q)?
4x?
-
9=
(2x)?
-
3?
a?
-
b?
=
(
a
+
b)(
a
-
b
)
(x+p)?-(x+q)?
=
(
2x
+
3
)(2x
-
3)
=[(x+p)+(x+q)][(x+p)
-(x+q)]
=(2x+p+q)(p-q)
三、精讲实练:应用平方差公式
例2、分解因式:
①x4-y4
②a3b-ab
解:
①x4-y4
=(x2)2-(y2)2=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y)
②a3b-ab=ab(a2-1)
=ab(a+1)(a-1)
若有公因式则先提公因式。然后再看能否用公式法。
分解因式,必须进行到每一个多项式都不能再分解为止。
(1)9a2-4b2;
(2)x2y-4y;
(3)(a+1)2-1;
(4)x4-1;
(5)(x+y+z)2-(x-y+z)2.
四、实练:应用平方进行分解因式
B
解析:
a2-9=(a+3)(a-3).故选B.
检测反馈
1.将a2-9分解因式的结果是
( )
A.(a+9)(a-9)
B.(a+3)(a-3)
C.(a+3)2
D.(a-3)2
五、达标检测
B
2.将(a-1)2-1分解因式,结果正确的是
( )
A.a(a-1)
B.a(a-2)
C.(a-2)(a-1)
D.(a-2)(a+1)
3.计算552-152的结果是
( )
A.40
B.1600
C.2400
D.2800
D
解析:
552-152
=(55+15)×(55-15)
=70×40
=2800.故选D.
4.用平方差公式分解因式.
(1)36-x
2
;
(2)-a
2+b
2
;
(3)x
2-16y
2;
(4)x
2y
2-z
2;
(1)
4x?-
m?n?
解:4x?-
m?n?
=(2x)?
-
(mn)?
=(2x+mn)(2x-mn)
解:
练一练!
注意:若有公因式则先提公因式。然后再看能否用公式法。
(1)1002-992
(2)682-672
(4)
5.52-4.52
8
15
(
)
2
7
15
(
)
2
-
(3)
看谁算的又快又准确!
比一比!
小结:我学会了什么?
1.如果多项式各项含有公因式,则第一步是提出这个公因式.
2.如果多项式各项没有公因式,则第一步考虑用公式分解因式.
3.第一步分解因式以后,所含的多项式还可以继续分解,则需要进一步分解因式.直到每个多项式因式都不能分解为止.
作业布置
小本公式法(1)
