沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(共21张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.7 直角三角形全等的判定 课件(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 196.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 06:18:28 | ||
图片预览




文档简介
(共21张PPT)
19.7直角三角形全等的判定
全等判定三条件,总得有边来实现,
已知元素图上标,边角关系清晰见,
三边对等最易找,两边一角需夹角,
两角一边任意边,角角边或角边角,
三个角或边边角,不能全等莫推导。
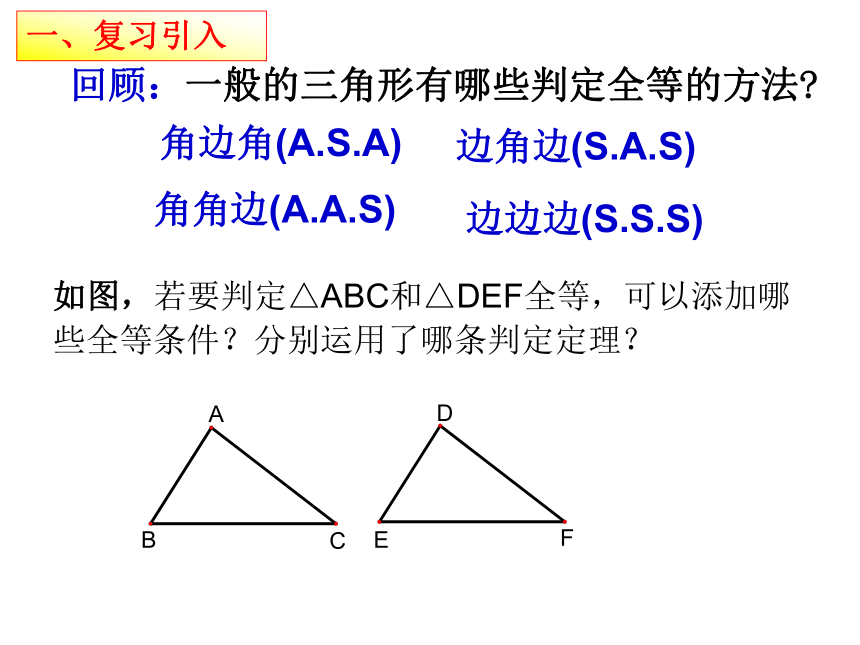
如图,若要判定△ABC和△DEF全等,可以添加哪些全等条件?分别运用了哪条判定定理?
回顾:一般的三角形有哪些判定全等的方法?
一、复习引入
角边角(A.S.A)
边角边(S.A.S)
角角边(A.A.S)
边边边(S.S.S)
对于一般的三角形“SSA”不可以证明三角形全等
二、新知探究
F
E
D
但直角三角形作为特殊的三角形,
能不能使用“边边角(S.S.A)”的判定方法呢?
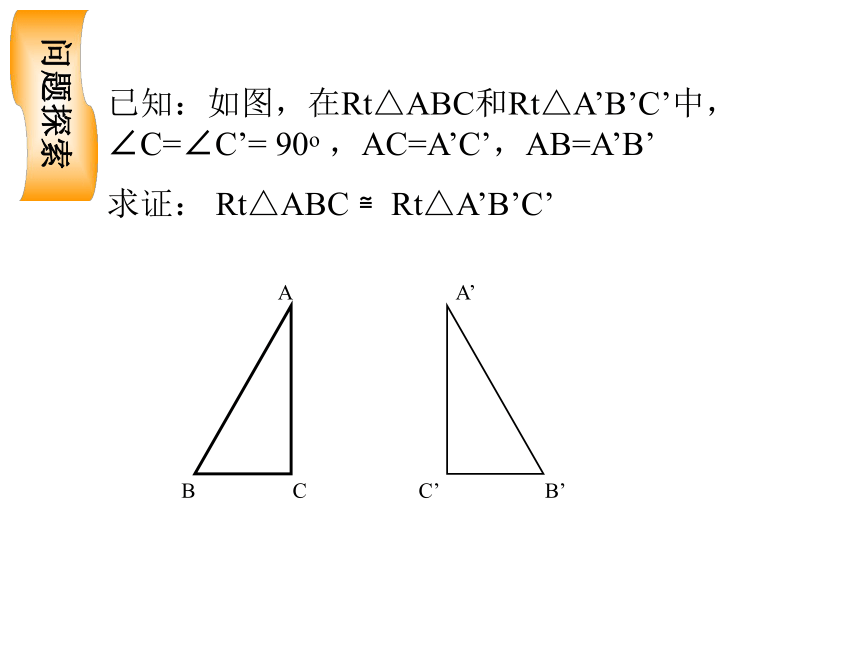
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AC=A’C’,AB=A’B’
求证:
Rt△ABC
≌Rt△A’B’C’
A’
C’
B’
A
B
C
问题探索
A’
C’
B’
A
B
C
关键
能够从已知条件中得到一个锐角对应相等。
证明
如图所示,把△ABC和△A’B’C’拼在一起,由于AC=A’C’,因此可使AC和A’C’重合,由于
∠ACB=∠A’C’B’=90o,因此点B、C、B’在一条直线上,于是得到了△ABB’。
A’
C’
B’
A’
C’
B’
A’
C’
B’
(A’)
(C’)
问题探索
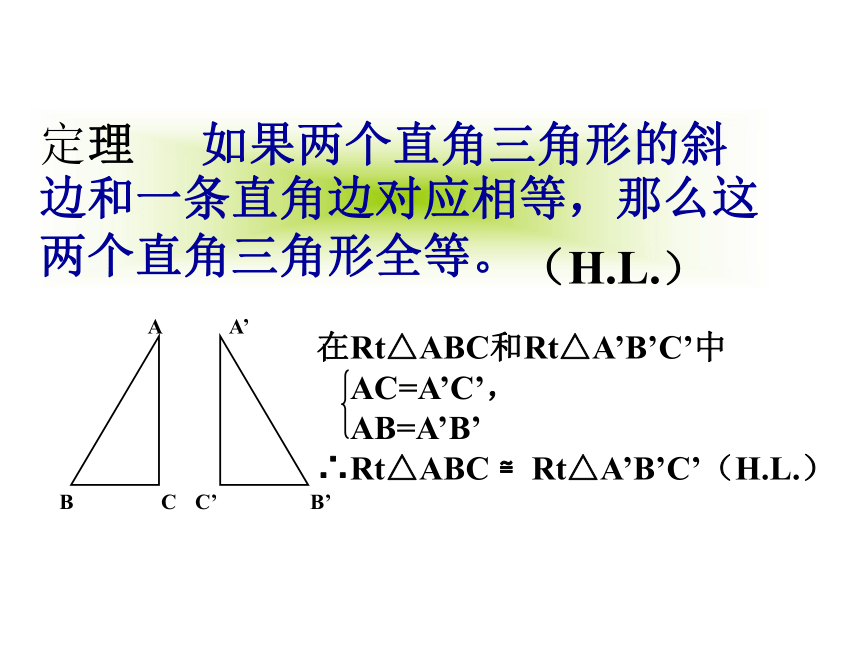
定理
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
A’
C’
B’
A
B
C
在Rt△ABC和Rt△A’B’C’中
AC=A’C’,
AB=A’B’
∴Rt△ABC
≌Rt△A’B’C’(H.L.)
(H.L.)
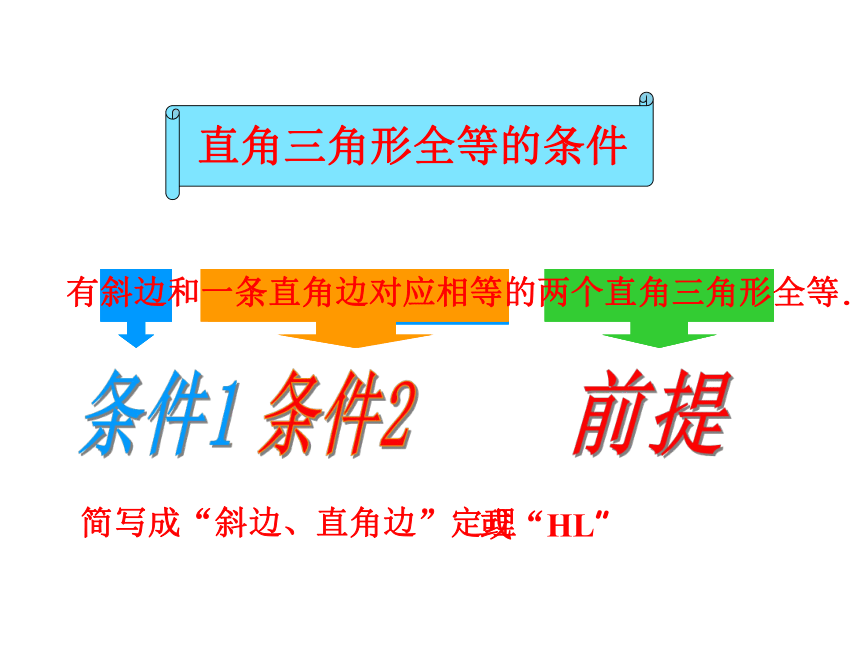
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”定理
或“HL”
前提
条件1
条件2
直角三角形全等的条件
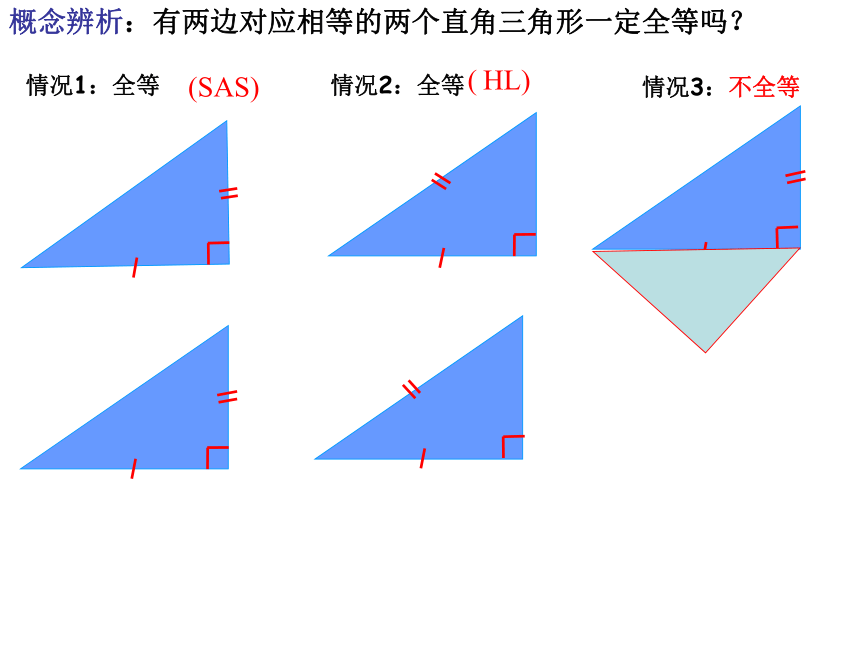
概念辨析:有两边对应相等的两个直角三角形一定全等吗?
情况1:全等
情况2:全等
(SAS)
(
HL)
情况3:不全等
练一练
如图,如图,把下列说明Rt△ABC≌Rt△DEF的条件或依据补充完整。(口答)
⑴_________∠A=∠D(A.S.A)
⑵AC=DF,_________(S.A.S)
⑶BC=EF,AB=DE(_____)
⑷AC=DF,_________(H.L)
⑸∠A=∠D,BC=EF(_____)
⑹_________,AC=DF(A.A.S)
AC=DF
BC=EF
H.L
AB=DE
A.A.S
∠B=∠E
适时小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
斜边,直角边
和直角
三、学以致用
求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
过点O、Q,作射线OQ.
∵QD⊥OA,QE⊥OB
(已知),
∴△QDO和△QEO都是直角三角形
(直角三角形的意义).
在Rt△QDO与Rt△QEO中,
QD=
QE
OQ=
(公共边),
∴Rt△QDO≌Rt△QEO
(H.L).
(已知),
OQ
三、学以致用
求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∴Rt△QDO≌Rt△QEO
(H.L)
∴∠1=∠2
(全等三角形的对应角相等)
∴OQ是∠AOB的平分线
(角平分线的意义)
即点Q在∠AOB的平分线上.
过点O、Q,作射线OQ
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
GO
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
B
C
E
B
C
D
∠ABC=∠ACB
AB=AC?
∟
∟
证明:
∵CE⊥AB,BD⊥AC
(已知),
∴△EBC和△DCB都是直角三角形.
在Rt△EBC与Rt△DCB中,
CE=BD
(已知),
BC=CB
(公共边),
∴Rt△EBC≌Rt△DCB
(H.L).
∴∠EBC=∠DCB
(全等…角相等).
∴AB=AC
(等角对等边).
即△ABC是等腰三角形.
(直角三角形的意义),
BACK
AB=AC?
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
A
B
D
A
C
E
∟
∟
BACK
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
B
C
E
B
C
D
A
B
D
A
C
E
∟
∟
法一
(A.A.S)
∟
∟
法二
(H.L)
已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:AB=AC
A
B
C
F
E
D
联结AF,AF平分∠BAC吗?为什么?
更上一层楼
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:(1)
DE=DF
(2)
EB=FC.
A
B
E
F
C
D
证明:
∵AD是∠BAC的平分线,
DE⊥AB,
DF⊥AC
(已知),
∴DE=DF
(在角的平分线上的点到这个角的两边的距离相等).
△BDE和△CDF都是直角三角形.
在Rt△BDE和Rt
△CDF中,
BD=CD(已知),
DE=DF
(已证),
∴Rt△BDE≌Rt△CDF(H.L).
∴EB=FC(全等三角形的对应边相等).
小试牛刀
F
A
D
E
B
C
∟
∟
2.已知:如图,EC⊥AB,FD⊥AB,垂足分别为点C、D,AF=BE,FD=EC
求证:AC=BD
五、课堂小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
运用“HL”定理时,
前提条件必须是___________,
然后依据_______和____________对应相等,
再证明两个直角三角形全等.
直角三角形
斜边
一条直角边
19.7直角三角形全等的判定
全等判定三条件,总得有边来实现,
已知元素图上标,边角关系清晰见,
三边对等最易找,两边一角需夹角,
两角一边任意边,角角边或角边角,
三个角或边边角,不能全等莫推导。
如图,若要判定△ABC和△DEF全等,可以添加哪些全等条件?分别运用了哪条判定定理?
回顾:一般的三角形有哪些判定全等的方法?
一、复习引入
角边角(A.S.A)
边角边(S.A.S)
角角边(A.A.S)
边边边(S.S.S)
对于一般的三角形“SSA”不可以证明三角形全等
二、新知探究
F
E
D
但直角三角形作为特殊的三角形,
能不能使用“边边角(S.S.A)”的判定方法呢?
已知:如图,在Rt△ABC和Rt△A’B’C’中,∠C=∠C’=
90o
,AC=A’C’,AB=A’B’
求证:
Rt△ABC
≌Rt△A’B’C’
A’
C’
B’
A
B
C
问题探索
A’
C’
B’
A
B
C
关键
能够从已知条件中得到一个锐角对应相等。
证明
如图所示,把△ABC和△A’B’C’拼在一起,由于AC=A’C’,因此可使AC和A’C’重合,由于
∠ACB=∠A’C’B’=90o,因此点B、C、B’在一条直线上,于是得到了△ABB’。
A’
C’
B’
A’
C’
B’
A’
C’
B’
(A’)
(C’)
问题探索
定理
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
A’
C’
B’
A
B
C
在Rt△ABC和Rt△A’B’C’中
AC=A’C’,
AB=A’B’
∴Rt△ABC
≌Rt△A’B’C’(H.L.)
(H.L.)
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”定理
或“HL”
前提
条件1
条件2
直角三角形全等的条件
概念辨析:有两边对应相等的两个直角三角形一定全等吗?
情况1:全等
情况2:全等
(SAS)
(
HL)
情况3:不全等
练一练
如图,如图,把下列说明Rt△ABC≌Rt△DEF的条件或依据补充完整。(口答)
⑴_________∠A=∠D(A.S.A)
⑵AC=DF,_________(S.A.S)
⑶BC=EF,AB=DE(_____)
⑷AC=DF,_________(H.L)
⑸∠A=∠D,BC=EF(_____)
⑹_________,AC=DF(A.A.S)
AC=DF
BC=EF
H.L
AB=DE
A.A.S
∠B=∠E
适时小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
斜边,直角边
和直角
三、学以致用
求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
过点O、Q,作射线OQ.
∵QD⊥OA,QE⊥OB
(已知),
∴△QDO和△QEO都是直角三角形
(直角三角形的意义).
在Rt△QDO与Rt△QEO中,
QD=
QE
OQ=
(公共边),
∴Rt△QDO≌Rt△QEO
(H.L).
(已知),
OQ
三、学以致用
求证:在一个角的内部(包括顶点)且到角的两边
距离相等的点,在这个角的平分线上.
O
B
A
1
2
D
∟
E
∟
Q
已知:如图,QD⊥OA,QE⊥OB,
垂足分别为点D、E,且QD=QE.
求证:点Q在∠AOB的平分线上.
证明:
∴Rt△QDO≌Rt△QEO
(H.L)
∴∠1=∠2
(全等三角形的对应角相等)
∴OQ是∠AOB的平分线
(角平分线的意义)
即点Q在∠AOB的平分线上.
过点O、Q,作射线OQ
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
GO
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
B
C
E
B
C
D
∠ABC=∠ACB
AB=AC?
∟
∟
证明:
∵CE⊥AB,BD⊥AC
(已知),
∴△EBC和△DCB都是直角三角形.
在Rt△EBC与Rt△DCB中,
CE=BD
(已知),
BC=CB
(公共边),
∴Rt△EBC≌Rt△DCB
(H.L).
∴∠EBC=∠DCB
(全等…角相等).
∴AB=AC
(等角对等边).
即△ABC是等腰三角形.
(直角三角形的意义),
BACK
AB=AC?
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
A
B
D
A
C
E
∟
∟
BACK
四、新知应用
已知:如图,△ABC中,BD⊥AC,CE⊥AB,
点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:△ABC是等腰三角形.
A
B
C
E
D
F
∟
∟
AB=AC?
B
C
E
B
C
D
A
B
D
A
C
E
∟
∟
法一
(A.A.S)
∟
∟
法二
(H.L)
已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.
求证:AB=AC
A
B
C
F
E
D
联结AF,AF平分∠BAC吗?为什么?
更上一层楼
1、已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.
求证:(1)
DE=DF
(2)
EB=FC.
A
B
E
F
C
D
证明:
∵AD是∠BAC的平分线,
DE⊥AB,
DF⊥AC
(已知),
∴DE=DF
(在角的平分线上的点到这个角的两边的距离相等).
△BDE和△CDF都是直角三角形.
在Rt△BDE和Rt
△CDF中,
BD=CD(已知),
DE=DF
(已证),
∴Rt△BDE≌Rt△CDF(H.L).
∴EB=FC(全等三角形的对应边相等).
小试牛刀
F
A
D
E
B
C
∟
∟
2.已知:如图,EC⊥AB,FD⊥AB,垂足分别为点C、D,AF=BE,FD=EC
求证:AC=BD
五、课堂小结
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
角边角
(A.S.A)
角角边
(A.A.S)
边角边
(S.A.S)
边边边
(S.S.S)
边边角
(H.L)
一般的三角形
直角三角形
全等三角形的判定方法
运用“HL”定理时,
前提条件必须是___________,
然后依据_______和____________对应相等,
再证明两个直角三角形全等.
直角三角形
斜边
一条直角边
