人教版数学九年级下册26.1.2 反比例函数的图象与性质——比例系数k的意义研究课教案
文档属性
| 名称 | 人教版数学九年级下册26.1.2 反比例函数的图象与性质——比例系数k的意义研究课教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 193.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 12:00:39 | ||
图片预览

文档简介
反比例函数的图象与性质——比例系数k的意义
教学目标:
理解和掌握反比例函数中比例系数k的代数意义和几何意义
灵活运用图象与性质解决综合问题
经历探索过程发展分析归纳和概括能力
教学重点:
反比例函数中比例系数k的几何意义的探究与运用
教学难点:
结合函数图象分析问题解决问题,k的几何意义的灵活运用
教学过程:
复习回顾
反比例函数的定义:形如的函数,
常用的等价形式:,即反比例函数图象上的点的横坐标纵坐标的乘积为常数k.
反比例函数的图象是双曲线,它的两支在每一个象限内的增减性取决于k的正负性.
引入新课
长/cm
1
2
3
4
5
宽/cm
2
1
下表是
10
个面积相等的矩形的长与宽,请补齐表格.
设∠A
为这
10
个矩形的公共角.画出这
10
个矩形,然后取∠A
的
10
个对角的顶点,并把这
10
个点用平滑的曲线顺次连接起来.
分析:从表中数据看出,长方形的面积为
5×2=10,这10个长方形的面积相等均为10.
从图象看出以这10个长方形的长宽为横纵坐标所得到的点可以连成了双曲线.
矩形的长
y
是宽
x
的反比例函数,即.
学习新知
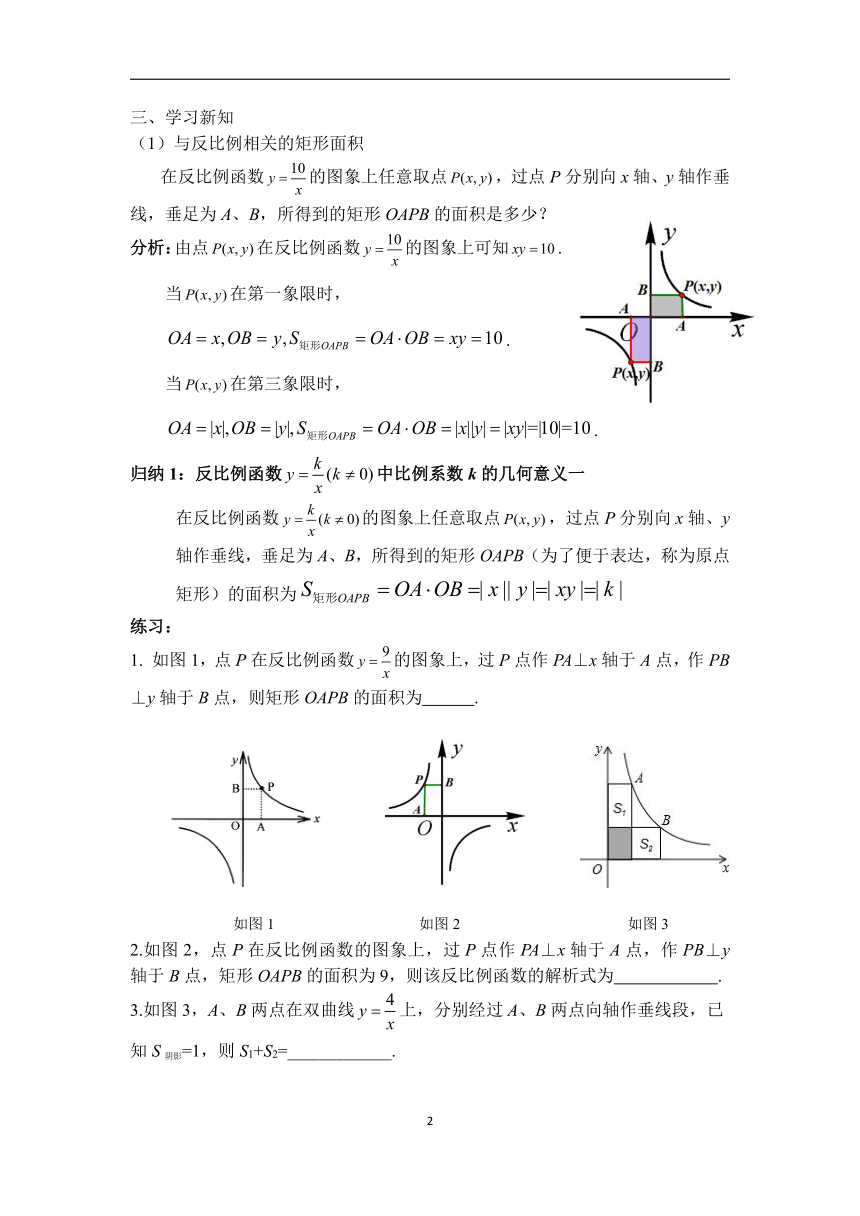
(1)与反比例相关的矩形面积
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,所得到的矩形OAPB的面积是多少?
分析:由点在反比例函数的图象上可知.
当在第一象限时,
.
当在第三象限时,
.
归纳1:反比例函数中比例系数k的几何意义一
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,所得到的矩形OAPB(为了便于表达,称为原点矩形)的面积为
练习:
1.
如图1,点P在反比例函数的图象上,过P点作PA⊥x轴于A点,作PB⊥y轴于B点,则矩形OAPB的面积为 .
如图1
如图2
如图3
2.如图2,点P在反比例函数的图象上,过P点作PA⊥x轴于A点,作PB⊥y轴于B点,矩形OAPB的面积为9,则该反比例函数的解析式为
.
3.如图3,A、B两点在双曲线上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=____________.
练习1是结论的直接应用,由k得出原点矩形的面积;练习2由原点矩形面积反推k,双曲线位于二四象限,需小心k取负数;练习3是综合运用,所有原点矩形面积均为4,从而=3.
参考答案:9,,6.
(2)与反比例相关的三角形面积
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,连接OP,所得到的直接三角形OAP,直角三角形OBP(为了便于表达,称为原点直角三角形)的面积是多少?
分析:将所求原点直角三角形的面积转化为已学的原点矩形的面积.
归纳2:
反比例函数中比例系数k的几何意义二
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,所得到的直角三角形的面积为
练习:
1.如图1,P是反比例函数的图象上一点,轴于点A.的面积为
.
图1
图2
反比例函数的图象如图所示,点M是该函数图象上一点,MN垂直于x轴于点N,如果△MON
的面积S△MON=2,则k的值为
.
分析:练习1是结论的直接应用,由k得出原点直角三角形的面积为;练习2由原点直角三角形的面积反推k,即,双曲线位于二四象限,需小心k取负数,.
四、运用新知
1.如图,
如果函数与y=的图象交于A、B两点,
过点A作AC垂直于y轴,
垂足为点C,
则△BOC的面积为
.
分析:根据本课所学可知,但计算△BOC的面积时无结论可用,需类比前面的方法,即利用反比例函数中.
联立两个函数解得
2.
如图,函数与的图象交于A、B两点,过A、B点分别作x轴和y轴作垂线垂足为D、E,两线相交于C点.则=
.
分析:根据本课所学可知,但计算矩形ODCE的面积时无结论可用,需类比前面的方法,即利用反比例函数中.
联立两个函数求解可知互为相反数.
则
从而可得.
3.
挑战练习
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N.
计算:(1)阴影部分面积,(2).
参考解答:
(1),
(2)=.
2
教学目标:
理解和掌握反比例函数中比例系数k的代数意义和几何意义
灵活运用图象与性质解决综合问题
经历探索过程发展分析归纳和概括能力
教学重点:
反比例函数中比例系数k的几何意义的探究与运用
教学难点:
结合函数图象分析问题解决问题,k的几何意义的灵活运用
教学过程:
复习回顾
反比例函数的定义:形如的函数,
常用的等价形式:,即反比例函数图象上的点的横坐标纵坐标的乘积为常数k.
反比例函数的图象是双曲线,它的两支在每一个象限内的增减性取决于k的正负性.
引入新课
长/cm
1
2
3
4
5
宽/cm
2
1
下表是
10
个面积相等的矩形的长与宽,请补齐表格.
设∠A
为这
10
个矩形的公共角.画出这
10
个矩形,然后取∠A
的
10
个对角的顶点,并把这
10
个点用平滑的曲线顺次连接起来.
分析:从表中数据看出,长方形的面积为
5×2=10,这10个长方形的面积相等均为10.
从图象看出以这10个长方形的长宽为横纵坐标所得到的点可以连成了双曲线.
矩形的长
y
是宽
x
的反比例函数,即.
学习新知
(1)与反比例相关的矩形面积
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,所得到的矩形OAPB的面积是多少?
分析:由点在反比例函数的图象上可知.
当在第一象限时,
.
当在第三象限时,
.
归纳1:反比例函数中比例系数k的几何意义一
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,所得到的矩形OAPB(为了便于表达,称为原点矩形)的面积为
练习:
1.
如图1,点P在反比例函数的图象上,过P点作PA⊥x轴于A点,作PB⊥y轴于B点,则矩形OAPB的面积为 .
如图1
如图2
如图3
2.如图2,点P在反比例函数的图象上,过P点作PA⊥x轴于A点,作PB⊥y轴于B点,矩形OAPB的面积为9,则该反比例函数的解析式为
.
3.如图3,A、B两点在双曲线上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=____________.
练习1是结论的直接应用,由k得出原点矩形的面积;练习2由原点矩形面积反推k,双曲线位于二四象限,需小心k取负数;练习3是综合运用,所有原点矩形面积均为4,从而=3.
参考答案:9,,6.
(2)与反比例相关的三角形面积
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,连接OP,所得到的直接三角形OAP,直角三角形OBP(为了便于表达,称为原点直角三角形)的面积是多少?
分析:将所求原点直角三角形的面积转化为已学的原点矩形的面积.
归纳2:
反比例函数中比例系数k的几何意义二
在反比例函数的图象上任意取点,过点P分别向x轴、y轴作垂线,垂足为A、B,所得到的直角三角形的面积为
练习:
1.如图1,P是反比例函数的图象上一点,轴于点A.的面积为
.
图1
图2
反比例函数的图象如图所示,点M是该函数图象上一点,MN垂直于x轴于点N,如果△MON
的面积S△MON=2,则k的值为
.
分析:练习1是结论的直接应用,由k得出原点直角三角形的面积为;练习2由原点直角三角形的面积反推k,即,双曲线位于二四象限,需小心k取负数,.
四、运用新知
1.如图,
如果函数与y=的图象交于A、B两点,
过点A作AC垂直于y轴,
垂足为点C,
则△BOC的面积为
.
分析:根据本课所学可知,但计算△BOC的面积时无结论可用,需类比前面的方法,即利用反比例函数中.
联立两个函数解得
2.
如图,函数与的图象交于A、B两点,过A、B点分别作x轴和y轴作垂线垂足为D、E,两线相交于C点.则=
.
分析:根据本课所学可知,但计算矩形ODCE的面积时无结论可用,需类比前面的方法,即利用反比例函数中.
联立两个函数求解可知互为相反数.
则
从而可得.
3.
挑战练习
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N.
计算:(1)阴影部分面积,(2).
参考解答:
(1),
(2)=.
2
