湘教版(2012)初中数学八年级上册 2.4 线段的垂直平分线 第1课时 教案
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册 2.4 线段的垂直平分线 第1课时 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 366.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 17:45:34 | ||
图片预览


文档简介
2.4?.1线段的垂直平分线(第一课时)?教学设计
一、教材分析?
线段的垂直平分线这节课是湘教版八年级上册第二章三角形第四节线段的垂直平分线第一课时的内容,线段的垂直平分线是几何中的重要概念。在几何证明、计算中,线段的垂直平分线的性质也有着重要的地位。?
二、学情分析?
在知识掌握上,学生已经学习了全等三角形,对轴对称图形的性质有所认识,因此在知识的过渡上不会有困难,只是对该结论的正确性会产生质疑。在心理上,八年级学生独立性和表现欲较强,希望得到老师和同伴的认可与肯定,体现自身价值,教师要抓住这一心理特征,积极鼓励,增强学生学习的主动性。?
三、教学目标分析?
(一)教学目标?
根据本节课的内容、学情分析和课程标准,我设计本节课的教学目标为:?知识技能:(1)经历线段的轴对称性质的探究过程,理解线段垂直平分线的概念。(2)探索线段垂直平分线的性质。过程与方法:探索掌握线段垂直平分线的性质定理及其逆定理。情感态度:通过研究解决问题的过程,积极参与数学活动,培养学生合作交流意识与探究精神。??
(二)教学重难点?
根据教学内容和学情我把“线段垂直平分线的概念;探索线段垂直平分线的性质”作为本节课的教学重点。?“探索线段的垂直平分线的性质”确定为本节课的难点?
四、教法学法分析?
(一)教学方法:?
《新课标》指出“学生是学习的主人,教师是学习的组织者、引导者、和合作者。”本课以学生的实验探究活动为主线,以突出重点、突破难点、发展学生数学素养为目的,采用以“探究式教学法”为主,讲授法、启发式教学、多媒体辅助教学等多种方法相结合。注重培养学生动手操作,主动探究及合作交流的能力。通过数学活动的经验,培养合情推理与初步的逻辑推理能力。注重学生的个性差异,因材施教,分层教学。
(二)学法指导:
本节课采用学生通过实验探究,自主探索,讨论交流,师生互动的学习方式,突出学生是学习的主体。
五、教学过程
(一)创设情境,导入新课
问题导入:如图,在河岸的一侧有相隔一段距离的A、B两个仓库,要在河岸边建造一个码头,使它到A、B两个仓库的距离相等,码头应建在什么位置?
(为了激发学生的学习兴趣,我设计了确定码头位置这个生活中的实际问题,导入新课。让学生意识到日常生活中许多问题都可以用数学知识来解决,体现了数学知识来源生活且应用于生活。)
(二)实验探究活动,学习新知
1、活动一:
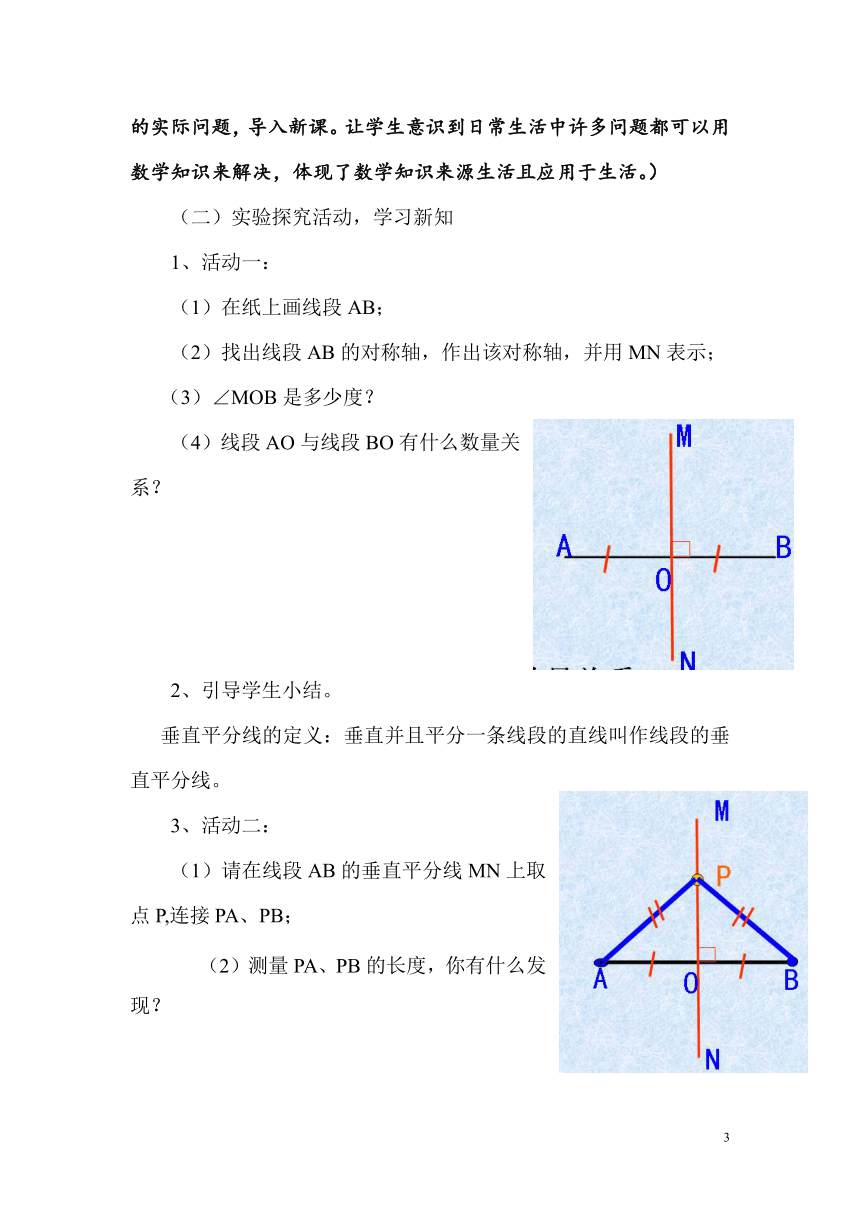
(1)在纸上画线段AB;
(2)找出线段AB的对称轴,作出该对称轴,并用MN表示;
(3)∠MOB是多少度?
(4)线段AO与线段BO有什么数量关系?
2、引导学生小结。
垂直平分线的定义:垂直并且平分一条线段的直线叫作线段的垂直平分线。
3、活动二:
(1)请在线段AB的垂直平分线MN上取点P,连接PA、PB;
(2)测量PA、PB的长度,你有什么发现?
3、启发引导学生得出平行线的性质
垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
(三)讲练结合,巩固新知
1、如图,△ABC中,BC的垂直平分线DE交AC于点D,交BC于点E,(1)若DB=11,则DC=
(2)若AD=4,DB=11,则AC=
2、【变式1】如图,△ABC中,AB=9cm,AC=15cm,BC的垂直平分线DE交AC于点D,交BC于点E,求△ABD的周长。
3、【变式2】如图,在△ABC中,AB<
AC,BC边上的垂直平分线DE交BC于点E,AC=15cm,ΔABD的周长是24cm,求AB的长。
(第一个题目是直接运用性质解决问题,比较简单,面向全体学生。我还设计了二个这类题目的变式题,目的让学生灵活动用性质定理进行解题。)
(四)效果检测?
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点.如果EC=7cm,那么ED=____cm;如果∠ECD=60°,那么∠EDC=________.
2.如图,等腰△ABC中,AB=AC,∠A=40°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于
.
3.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
4、让学生用所学知识解决情境导入的数学问题。
(为了检测学生学习情况,我设计了当堂检测,并让学生解决我情境导入的问题。)
(五)课堂小结
1、这节课你收获了哪些知识?
2、你在学习过程中,哪些知识还没有掌握好?
(在学生们共同归纳总结本节课的过程中,让学生获得数学思考上的提高和感受成功的喜悦并进一步系统地完善本节课的知识。?)
(六)作业?
作业:教材P72
第1、3、6题
教学后记:本节课学生经历了“从生活中发现问题,提出问题,通过活动探究,生成知识,运用知识解决问题,体会生活中处处有数学,并获得成功体验,”符合学生认知规律,让学生成为学习的主体。?
5
一、教材分析?
线段的垂直平分线这节课是湘教版八年级上册第二章三角形第四节线段的垂直平分线第一课时的内容,线段的垂直平分线是几何中的重要概念。在几何证明、计算中,线段的垂直平分线的性质也有着重要的地位。?
二、学情分析?
在知识掌握上,学生已经学习了全等三角形,对轴对称图形的性质有所认识,因此在知识的过渡上不会有困难,只是对该结论的正确性会产生质疑。在心理上,八年级学生独立性和表现欲较强,希望得到老师和同伴的认可与肯定,体现自身价值,教师要抓住这一心理特征,积极鼓励,增强学生学习的主动性。?
三、教学目标分析?
(一)教学目标?
根据本节课的内容、学情分析和课程标准,我设计本节课的教学目标为:?知识技能:(1)经历线段的轴对称性质的探究过程,理解线段垂直平分线的概念。(2)探索线段垂直平分线的性质。过程与方法:探索掌握线段垂直平分线的性质定理及其逆定理。情感态度:通过研究解决问题的过程,积极参与数学活动,培养学生合作交流意识与探究精神。??
(二)教学重难点?
根据教学内容和学情我把“线段垂直平分线的概念;探索线段垂直平分线的性质”作为本节课的教学重点。?“探索线段的垂直平分线的性质”确定为本节课的难点?
四、教法学法分析?
(一)教学方法:?
《新课标》指出“学生是学习的主人,教师是学习的组织者、引导者、和合作者。”本课以学生的实验探究活动为主线,以突出重点、突破难点、发展学生数学素养为目的,采用以“探究式教学法”为主,讲授法、启发式教学、多媒体辅助教学等多种方法相结合。注重培养学生动手操作,主动探究及合作交流的能力。通过数学活动的经验,培养合情推理与初步的逻辑推理能力。注重学生的个性差异,因材施教,分层教学。
(二)学法指导:
本节课采用学生通过实验探究,自主探索,讨论交流,师生互动的学习方式,突出学生是学习的主体。
五、教学过程
(一)创设情境,导入新课
问题导入:如图,在河岸的一侧有相隔一段距离的A、B两个仓库,要在河岸边建造一个码头,使它到A、B两个仓库的距离相等,码头应建在什么位置?
(为了激发学生的学习兴趣,我设计了确定码头位置这个生活中的实际问题,导入新课。让学生意识到日常生活中许多问题都可以用数学知识来解决,体现了数学知识来源生活且应用于生活。)
(二)实验探究活动,学习新知
1、活动一:
(1)在纸上画线段AB;
(2)找出线段AB的对称轴,作出该对称轴,并用MN表示;
(3)∠MOB是多少度?
(4)线段AO与线段BO有什么数量关系?
2、引导学生小结。
垂直平分线的定义:垂直并且平分一条线段的直线叫作线段的垂直平分线。
3、活动二:
(1)请在线段AB的垂直平分线MN上取点P,连接PA、PB;
(2)测量PA、PB的长度,你有什么发现?
3、启发引导学生得出平行线的性质
垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
(三)讲练结合,巩固新知
1、如图,△ABC中,BC的垂直平分线DE交AC于点D,交BC于点E,(1)若DB=11,则DC=
(2)若AD=4,DB=11,则AC=
2、【变式1】如图,△ABC中,AB=9cm,AC=15cm,BC的垂直平分线DE交AC于点D,交BC于点E,求△ABD的周长。
3、【变式2】如图,在△ABC中,AB<
AC,BC边上的垂直平分线DE交BC于点E,AC=15cm,ΔABD的周长是24cm,求AB的长。
(第一个题目是直接运用性质解决问题,比较简单,面向全体学生。我还设计了二个这类题目的变式题,目的让学生灵活动用性质定理进行解题。)
(四)效果检测?
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点.如果EC=7cm,那么ED=____cm;如果∠ECD=60°,那么∠EDC=________.
2.如图,等腰△ABC中,AB=AC,∠A=40°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于
.
3.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
4、让学生用所学知识解决情境导入的数学问题。
(为了检测学生学习情况,我设计了当堂检测,并让学生解决我情境导入的问题。)
(五)课堂小结
1、这节课你收获了哪些知识?
2、你在学习过程中,哪些知识还没有掌握好?
(在学生们共同归纳总结本节课的过程中,让学生获得数学思考上的提高和感受成功的喜悦并进一步系统地完善本节课的知识。?)
(六)作业?
作业:教材P72
第1、3、6题
教学后记:本节课学生经历了“从生活中发现问题,提出问题,通过活动探究,生成知识,运用知识解决问题,体会生活中处处有数学,并获得成功体验,”符合学生认知规律,让学生成为学习的主体。?
5
同课章节目录
